Assuming the length of a chain to be L and coefficient of static friction μ. Compute the maximum length of the chain which can be held outside a table without sliding.
To solve the problem of finding the maximum length of a chain that can be held outside a table without sliding, we can follow these steps:
1. Define Variables:
- Let the total length of the chain be L.
- Let the length of the chain hanging off the table be x.
- The length of the chain on the table will then be L−x.
- Let the coefficient of static friction be μ.
2. Identify Forces:
- The weight of the chain hanging off the table is given by W=mg, where m is the mass of the hanging part of the chain. Since the mass per unit length is constant, we can express the mass of the hanging part as m=ML⋅x, where M is the total mass of the chain.
- The normal force N acting on the part of the chain on the table is equal to the weight of the chain that is on the table, which is N=ML⋅(L−x)⋅g.
3. Frictional Force:
- The maximum static frictional force that can act on the chain on the table is given by:
Ffriction=μN=μ(ML⋅(L−x)⋅g)
4. Equilibrium Condition:
- For the chain to be in equilibrium, the frictional force must balance the weight of the hanging part of the chain:
Ffriction=W
- Therefore, we can set up the equation:
μ(ML⋅(L−x)⋅g)=ML⋅x⋅g
5. Simplifying the Equation:
- Cancel ML⋅g from both sides (assuming M≠0 and g≠0):
μ(L−x)=x
6. Rearranging the Equation:
- Rearranging gives:
μL−μx=x
- Combine like terms:
μL=x+μx
μL=x(1+μ)
7. Solving for x:
- Finally, solve for x:
x=μL1+μ
Final Result:
The maximum length of the chain that can be held outside the table without sliding is:
x=μL1+μ
- Let the total length of the chain be L.
- Let the length of the chain hanging off the table be x.
- The length of the chain on the table will then be L−x.
- Let the coefficient of static friction be μ.
- The weight of the chain hanging off the table is given by W=mg, where m is the mass of the hanging part of the chain. Since the mass per unit length is constant, we can express the mass of the hanging part as m=ML⋅x, where M is the total mass of the chain.
- The normal force N acting on the part of the chain on the table is equal to the weight of the chain that is on the table, which is N=ML⋅(L−x)⋅g.
- The maximum static frictional force that can act on the chain on the table is given by:
Ffriction=μN=μ(ML⋅(L−x)⋅g)
- For the chain to be in equilibrium, the frictional force must balance the weight of the hanging part of the chain:
Ffriction=W
- Therefore, we can set up the equation:
μ(ML⋅(L−x)⋅g)=ML⋅x⋅g
- Cancel ML⋅g from both sides (assuming M≠0 and g≠0):
μ(L−x)=x
- Rearranging gives:
μL−μx=x
- Combine like terms:
μL=x+μx
μL=x(1+μ)
- Finally, solve for x:
x=μL1+μ
The maximum length of the chain that can be held outside the table without sliding is:
x=μL1+μ
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-I
Explore 52 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-II
Explore 112 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
Similar Questions
A uniform rope of length l lies on a table . If the coefficient of friction is μ , then the maximum length l1 of the part of this rope which can overhang from the edge of the table without sliding down is :
1μ
lμ+1
μl1+μ
μl1−μ
View SolutionA heavy uniform chain lies on horizontal table top. If the coefficient of friction 0.25, then the maximum fraction of length of the chain that can hang over on one edge of the table is
View Solution
Knowledge Check
A block of mass m is at rest on an inclined plane. The coefficient of static friction is μ. The maximum angle of incline before the block begins to slide down is :
Atan−1(μ/m)Btan−1(μ)Ctan−1(μ/2)Dcos−1(μ)A heavy uniform chain lies on horizontal table top. If the coefficient of friction between the chain and the table surface is 0.25, then the maximum fraction of the length of the chain that can hang over one edge of the table is
A0.2B0.25C0.35D0.15
A car has to move on a level turn of radius 45 m. If the coefficient of static friction between the tyre and the road is μs=2.0, find the maximum speed the car can take without skidding.
View SolutionA homogoneous chain of length L lies on a table. The coefficient of friction between the chain and the table is μ. The maximum length which can hang over the table in equilibrium is
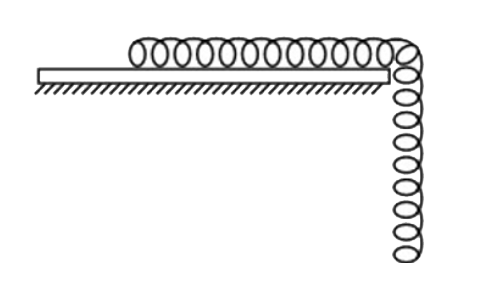
View SolutionA chain is placed on a rough table, partially hanging, as shown in the figure. The coefficient of static friction between the chain and the table is μ = 0.4. If the maximum possible length of the hanging part is x and the length of the chain is L, then what is the value of Lx?
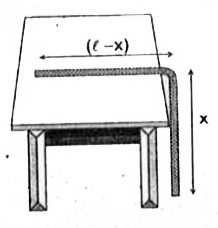
View SolutionA uniform chain of mass m and length I is kept on the table with a part of it overhanging (see figure). If the coefficient of friction between the table and the chain is 1/3 then find the maximum length of the chain that can overhang such that the chain remain in equilibrium.
View SolutionA rough inclined plane is inclined at 30° to the horizontal as shown in the figure. A uniform chain of length L is partly on the inclined plane and partly hanging from the top of the incline. If the coefficient offriction between chain and inclined plane is μ, the maximum length of the lianging part to prevent the chain from falling vertically is:
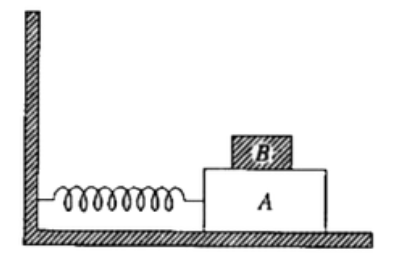
View SolutionIn Fig. A is a large block which executes shm by sliding across a frictionless surface with a frequency n. The block B is at rest on the surface of the block μs The coefficient of static friction between the two is H. Find the maximum amplitude of oscillation of the system so that the block B does not slip.
View Solution