A boy of mass 40 kg is hanging from the horizontal branch of a tree. The tension in his arms is minimum when the angle between the arms is:-
0∘
90∘
120∘
180∘
The correct Answer is:A
To solve the problem of finding the angle between the boy's arms when the tension in his arms is minimum, we can follow these steps:
Step 1: Understand the Forces Acting on the Boy
The boy is hanging from a horizontal branch, and the forces acting on him include:
- The gravitational force (weight) acting downwards, which is equal to mg, where m=40kg and g=10m/s2. Therefore, mg=40×10=400N.
- The tension in his arms, which we will denote as T.
Step 2: Define the Angle Between the Arms
Let the angle between the boy's arms be 2θ. This means that each arm makes an angle θ with the vertical.
Step 3: Resolve the Tension into Components
The tension T in each arm can be resolved into two components:
- A vertical component: Tcosθ
- A horizontal component: Tsinθ
Step 4: Set Up the Vertical Force Balance
Since the boy is in equilibrium (not moving), the total upward force must equal the downward force due to gravity. Therefore, we can write:
2Tcosθ=mg
Substituting mg=400N:
2Tcosθ=400
Step 5: Solve for Tension
From the above equation, we can solve for the tension T:
T=4002cosθ=200cosθ
Step 6: Minimize the Tension
To find the angle that minimizes the tension, we need to maximize cosθ. The maximum value of cosθ is 1, which occurs when θ=0∘.
Step 7: Conclusion
Thus, the angle between the boy's arms is:
2θ=2×0∘=0∘
This means the arms are straight down, and the tension in the arms is at its minimum.
Final Answer
The angle between the arms is 0∘.
---
The boy is hanging from a horizontal branch, and the forces acting on him include:
- The gravitational force (weight) acting downwards, which is equal to mg, where m=40kg and g=10m/s2. Therefore, mg=40×10=400N.
- The tension in his arms, which we will denote as T.
Let the angle between the boy's arms be 2θ. This means that each arm makes an angle θ with the vertical.
The tension T in each arm can be resolved into two components:
- A vertical component: Tcosθ
- A horizontal component: Tsinθ
Since the boy is in equilibrium (not moving), the total upward force must equal the downward force due to gravity. Therefore, we can write:
2Tcosθ=mg
Substituting mg=400N:
2Tcosθ=400
From the above equation, we can solve for the tension T:
T=4002cosθ=200cosθ
To find the angle that minimizes the tension, we need to maximize cosθ. The maximum value of cosθ is 1, which occurs when θ=0∘.
Thus, the angle between the boy's arms is:
2θ=2×0∘=0∘
This means the arms are straight down, and the tension in the arms is at its minimum.
The angle between the arms is 0∘.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I
52 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
Similar Questions
A boy is hanging from a horizontal branch of a tree. The tension in the arms will be maximum when the angle between the arms is
View SolutionA boy of mass 40 kg climbs up a rope with an acceleration of 2ms−2 . What is the tension in the rope ?
View SolutionA massless rope of length 100m and of breaking strength 108N is hanging from the branch of a tree. A monkey of mass 6 kg is trying to climb up the rope starting from rest. Find the shortes time in which monkey can climb the full length of rope with uniform acceleration so that the string will not break ?
View SolutionA boy of weight 25kg slides down a rope hanging from the branch of a tree. If the force of friction against him is 50N, the boy's acceleration is (g=10ms−2)
View SolutionA block A of mass 2kg rests on another block B of mass 8kg which rests on a horizontal floor. The coefficient of friction between A and B is 0.2 while that between B and floor is 0.5.When a horizontal floor F of 25N is applied on the block B the force of friction between A and B is
View SolutionA block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
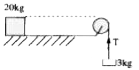
View SolutionA body of mass 20kg is moving on a rough horizontal plane. A block of mass 3kg is connected to the 20 kg mass by a string of negligible mass through a smooth pulley as shown in the figure. The tension in the string is 27 N. The coefficient of kinetic friction between the heavier mass and the surface is (g = 10m/s2)
View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

View Solution
