A block of mass Mis pulled vertically upward through a rope of mass m by applying force F on one end of the rope. What force does the rope exert on the block?
mFM+m
MFM+m
mMF
MmF
To find the force that the rope exerts on the block, we can follow these steps:
Step 1: Identify the Forces Acting on the Block
The forces acting on the block of mass M are:
- The gravitational force acting downward, which is Mg.
- The tension T in the rope acting upward.
Step 2: Apply Newton's Second Law
According to Newton's second law, the net force acting on the block is equal to the mass of the block times its acceleration:
Fnet=Ma
Where Fnet=T−Mg.
Step 3: Write the Equation for the Block
From the forces acting on the block, we can write:
T−Mg=Ma
Rearranging this gives:
T=Ma+Mg
T=M(a+g)
Step 4: Analyze the Rope
The rope has a mass m and is also being accelerated. The total mass being accelerated (block + rope) is M+m. The force F applied to the rope must overcome the weight of both the block and the rope.
Step 5: Write the Equation for the Rope
For the entire system (block + rope), we can write:
F−(M+m)g=(M+m)a
Rearranging gives:
F=(M+m)a+(M+m)g
F=(M+m)(a+g)
Step 6: Solve for Acceleration
From the equation T=M(a+g) and F=(M+m)(a+g), we can find the acceleration a:
a=FM+m−g
Step 7: Substitute Back to Find Tension
Now, substituting a back into the equation for tension T:
T=M(FM+m)
Step 8: Final Expression for Tension
Thus, the force that the rope exerts on the block is:
T=MFM+m
Conclusion
The force that the rope exerts on the block is given by:
T=MFM+m
The forces acting on the block of mass M are:
- The gravitational force acting downward, which is Mg.
- The tension T in the rope acting upward.
According to Newton's second law, the net force acting on the block is equal to the mass of the block times its acceleration:
Fnet=Ma
Where Fnet=T−Mg.
From the forces acting on the block, we can write:
T−Mg=Ma
Rearranging this gives:
T=Ma+Mg
T=M(a+g)
The rope has a mass m and is also being accelerated. The total mass being accelerated (block + rope) is M+m. The force F applied to the rope must overcome the weight of both the block and the rope.
For the entire system (block + rope), we can write:
F−(M+m)g=(M+m)a
Rearranging gives:
F=(M+m)a+(M+m)g
F=(M+m)(a+g)
From the equation T=M(a+g) and F=(M+m)(a+g), we can find the acceleration a:
a=FM+m−g
Now, substituting a back into the equation for tension T:
T=M(FM+m)
Thus, the force that the rope exerts on the block is:
T=MFM+m
The force that the rope exerts on the block is given by:
T=MFM+m
Similar Questions
A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m . Force F is applied at one end of rope. The force which the rope exerts on the block is:
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope, the force exerted by the rope on the block is
View Solution
Knowledge Check
A block of mass M is pulled along horizontal firctionless surface by a rop of mass m. Force P is applied at one end of rope. The force which the rope exerts on the block is
APM−mBPM(m+M)CPM(m+M)DPMM−m
A block of mass m is pulled by a uniform chain of mass m tied to it by applying a force F at the other end of the chain.The tension at a point P which is at a distance of quarter of the length of the chain from the free end,will be

View SolutionA force F is applied on a block of mass M. The block is displaced through a distance d in the direction of the force. What is the work done by the force on the block? Does the internal energy change because of this work?
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point

View SolutionA block is lying on the horizontal frictionless surface. One end of a uniform rope is fixed to the block which is pulled in the horizontal direction by applying a force F at the other end. If the mass of the rope is half the mass of the block. The tension in the middle of the rope will be
View SolutionA mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45∘ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g=10ms−2)
View SolutionA mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45∘ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g=10ms−2)
View SolutionTwo blocks of masses M and xM are pulled vertically upward with force F as shown in the figure . If the tension in string connecting two blocks is F3 then find the value of x .
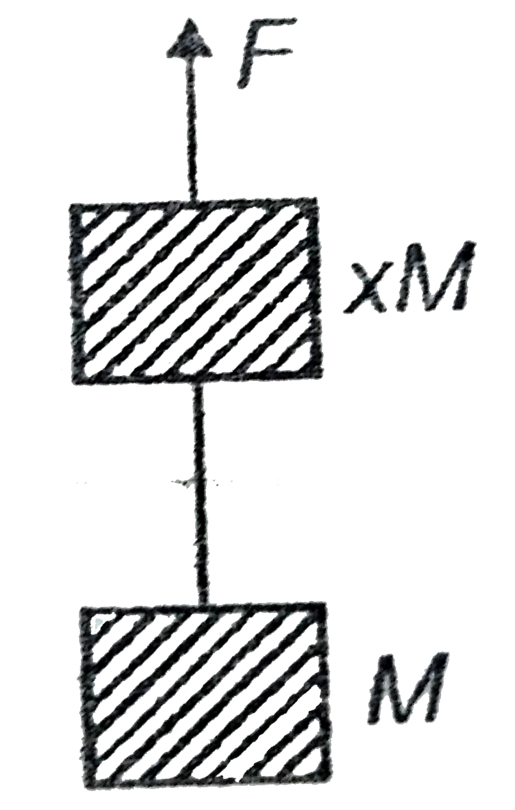
View Solution
