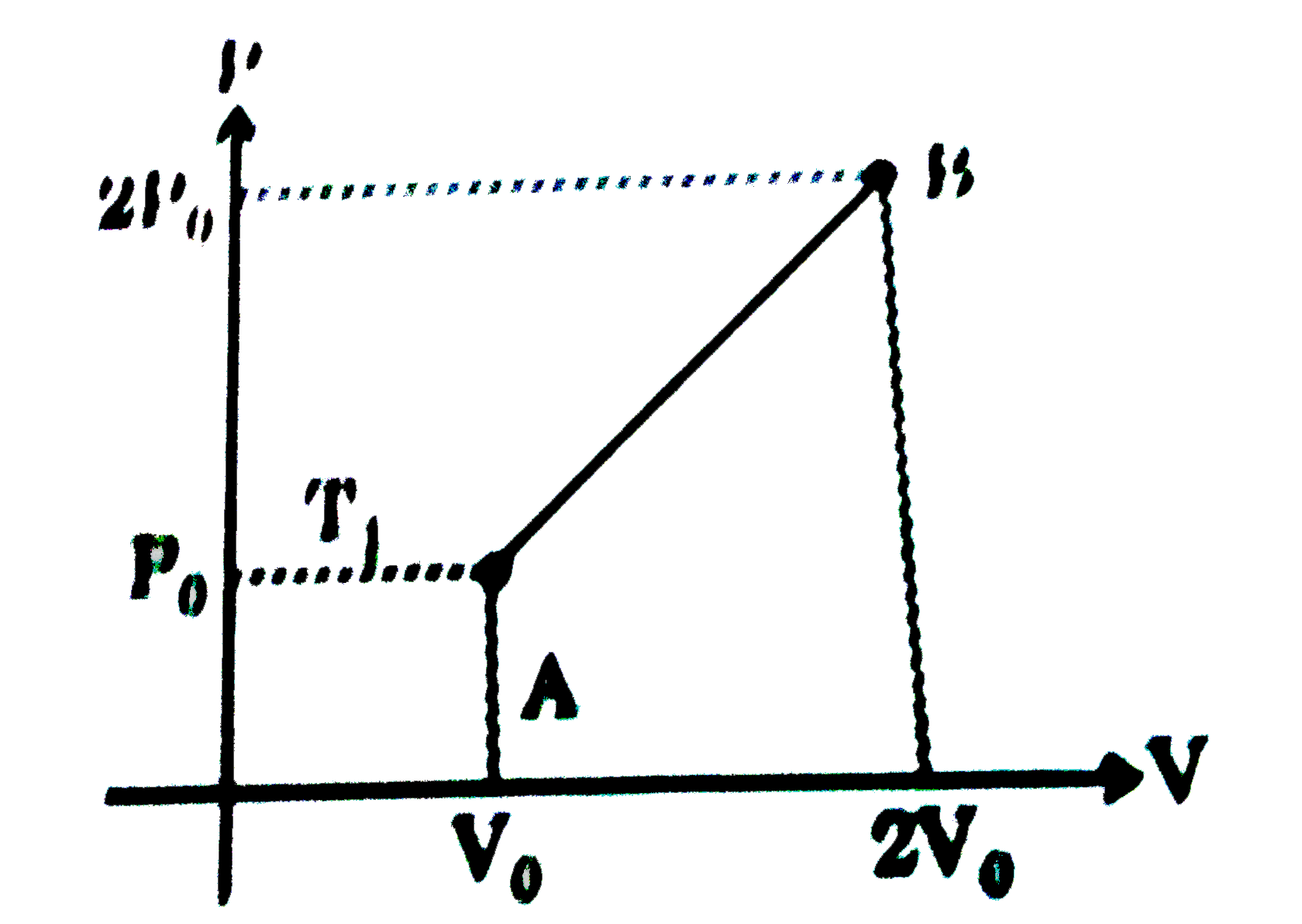
One mole of gas is taken from state A to state B as shown in figure. Work done by the gas is α×10βJ. Find the value of α+β.
(Given: T1=320K,R=253)
_S01_126_Q01.png)
The correct Answer is:7
Work done = 12[P0+2P0][2V0−V0]=32P0V0
and P0V0=R×320
So work done 32×R×320=32×253×320=4000J=4×103J⇒α+β=4+3=7
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -02
82 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Knowledge Check
An ideal gas change from state a to state b as shown in Fig. what is the work done by the gas in the process?
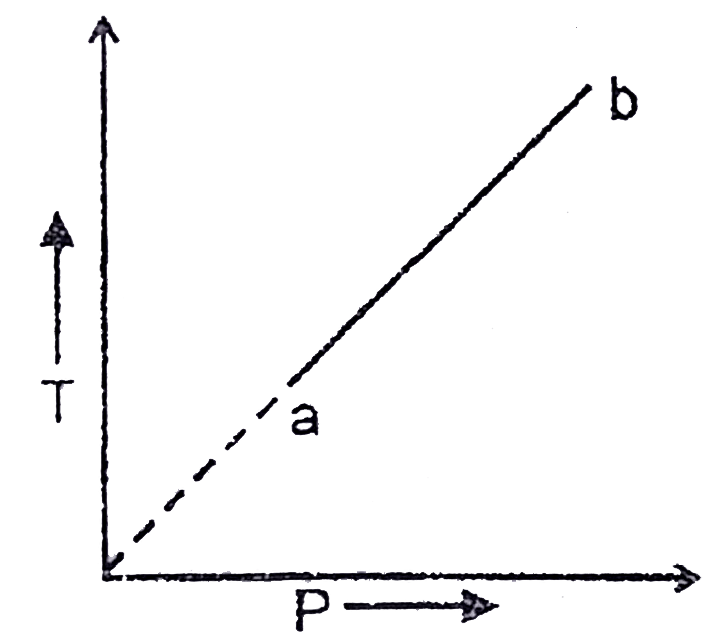 AZeroBPositiveCNegativeDInfinite
AZeroBPositiveCNegativeDInfiniteAn ideal gas change from state a to state b as shown in Fig. what is the work done by the gas in the process?
 AzeroBpositiveCnegativeDinfinite
AzeroBpositiveCnegativeDinfinite
One mole of a monoatomic gas is carried along process ABCDEA as shown in the diagram. The net work done by gas is (0.x)J. Find value of x.
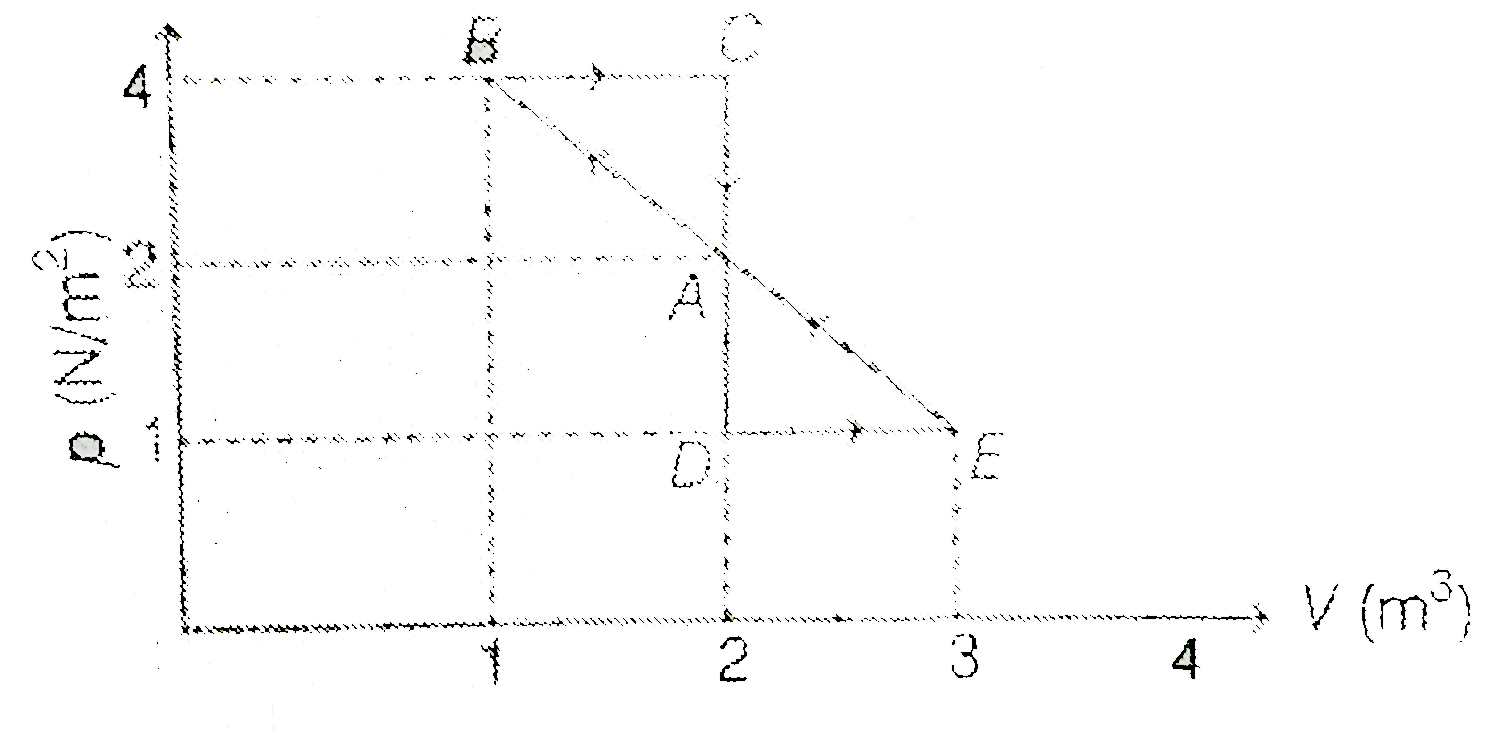
View SolutionOne mole of a monoatomic gas is carried along process ABCDEA as shown in the diagram. The net work done by gas is (0.x)J. Find value of x.

View Solution1.0 mol of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in figure. Calculate the work done for the expansion of gas from state (1) to state (2) as 298 K.

View Solution1.0 mol of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in figure. Calculate the work done for the expansion of gas from state (1) to state (2) at 298 K.
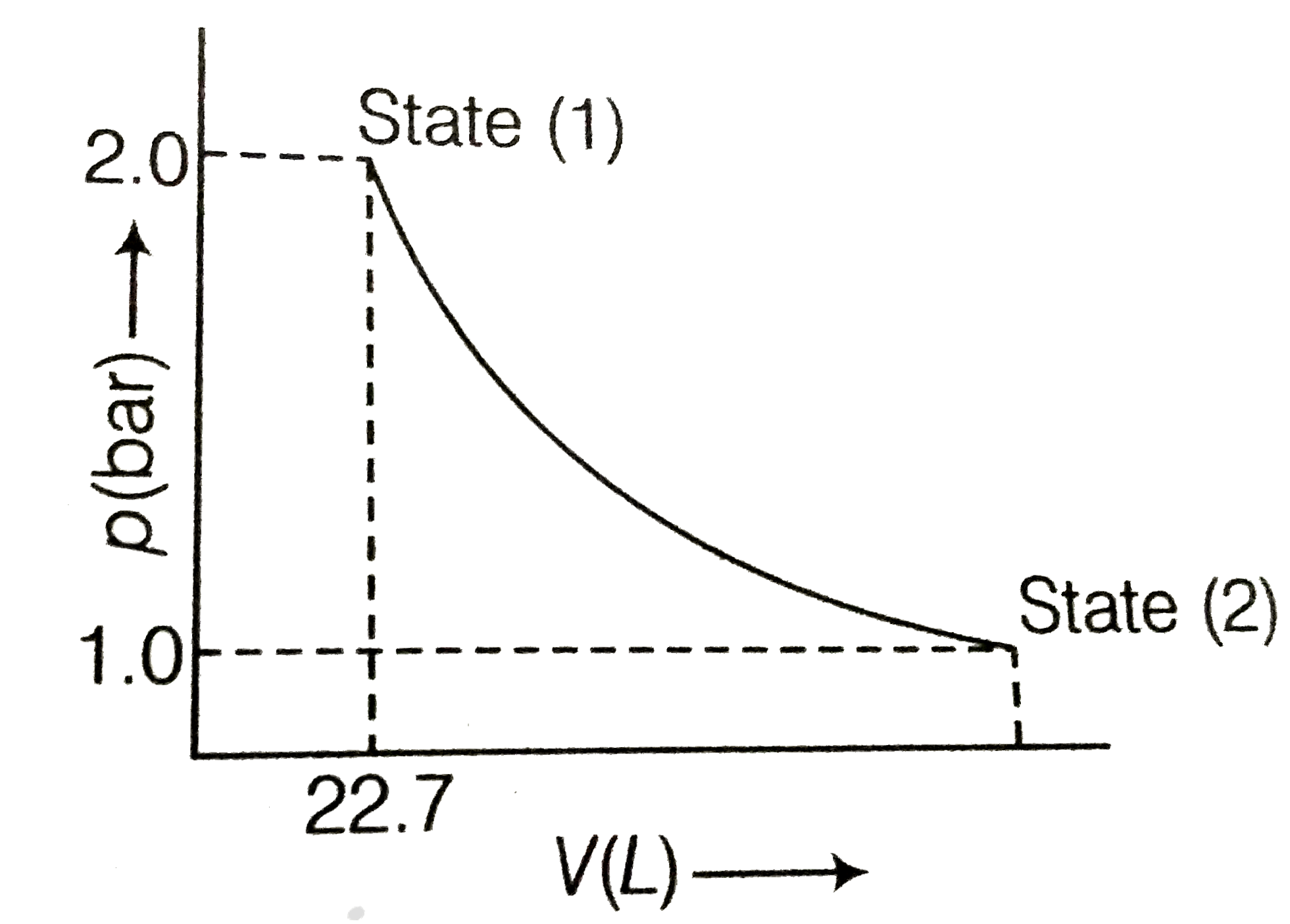
View Solution1.0 mol of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in figure. Calculate the work done for the expansion of gas from state (1) to state (2) as 298 K.

View SolutionThe internal energy of monatomic ideal gas is 1.5(MR)T. One mole of helium is kept in a cylinder of cross-section 8.5cm2. The cylinder is closed by a light frictionless piston. The gas is heated slowly in a process during which a total of 42J heat is given to the gas. The temperature of the gas rises by 2C. The distance moved by the piston is given as α×10β meter. Find the value of (α+β). [Take universal gas constant R=253Jmol−1K−1. atmospheric pressure =100(kPa)]
View Solution