The relation between internal energy U, pressure P and volume V of a gas in an adiabatic processes is : U=a+bPV where a = b = 3 . Calculate the greatest integer of the ratio of specific heats [γ] .
The correct Answer is:1
To solve the problem, we start with the given relation between internal energy U, pressure P, and volume V of the gas in an adiabatic process:
U=a+bPV
where a=3 and b=3.
Step 1: Write down the expression for internal energy.
Given:
U=3+3PV
Step 2: Use the first law of thermodynamics for an adiabatic process.
For an adiabatic process, the heat exchange dq=0. According to the first law of thermodynamics:
dq=dU+PdV=0
This implies:
dU+PdV=0⇒dU=−PdV
Step 3: Differentiate the expression for internal energy.
Differentiating U:
dU=dUdPdP+dUdVdV
From our expression for U:
dU=3⋅d(PV)=3(PdV+VdP)
Thus:
dU=3PdV+3VdP
Step 4: Set the expressions for dU equal.
From the first law:
3PdV+3VdP=−PdV
Rearranging gives:
3PdV+PdV+3VdP=0
(3+1)PdV+3VdP=0
4PdV+3VdP=0
Step 5: Rearranging the equation.
Dividing through by PV:
4VdV+3PdP=0
Step 6: Integrate the equation.
This can be rearranged to:
dVV=−34dPP
Integrating both sides gives:
lnV=−34lnP+C
Exponentiating:
V43P3=K
where K is a constant.
Step 7: Relate to the specific heats.
For an ideal gas, the relationship between specific heats γ is given by:
γ=CpCv
From the derived equation, we have:
PV43=constant
This indicates that:
γ=b+1b=43
Step 8: Calculate the greatest integer of γ.
Calculating γ:
γ=43≈1.33
Thus, the greatest integer of γ is:
⌊γ⌋=1
Final Answer:
The greatest integer of the ratio of specific heats γ is 1.
---
Given:
U=3+3PV
For an adiabatic process, the heat exchange dq=0. According to the first law of thermodynamics:
dq=dU+PdV=0
This implies:
dU+PdV=0⇒dU=−PdV
Differentiating U:
dU=dUdPdP+dUdVdV
From our expression for U:
dU=3⋅d(PV)=3(PdV+VdP)
Thus:
dU=3PdV+3VdP
From the first law:
3PdV+3VdP=−PdV
Rearranging gives:
3PdV+PdV+3VdP=0
(3+1)PdV+3VdP=0
4PdV+3VdP=0
Dividing through by PV:
4VdV+3PdP=0
This can be rearranged to:
dVV=−34dPP
Integrating both sides gives:
lnV=−34lnP+C
Exponentiating:
V43P3=K
where K is a constant.
For an ideal gas, the relationship between specific heats γ is given by:
γ=CpCv
From the derived equation, we have:
PV43=constant
This indicates that:
γ=b+1b=43
Calculating γ:
γ=43≈1.33
Thus, the greatest integer of γ is:
⌊γ⌋=1
The greatest integer of the ratio of specific heats γ is 1.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -02
82 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
The relation between the internal energy U adiabatic constant γ is
View SolutionThe relation between the internal energy (U) versus temeperature (T) for a 3 mole ideal gas in an isochoric process is given as U=α+βT where α and β are constant. If the specific heat capacity of the gas for above process is βm find the value of m.
View Solution
Knowledge Check
The relation between internal energy U, pressure P and volume V of a gas in an adiabatic process is
U=a+bPV where a and b are constants. What is the effective value of adiabatic constant γ ?A1. abB2. b+1bC3. a+1aD4. ba
The relation between U, p and V for an ideal gas in an adiabatic process is given by relation U=a+bpV. Find the value of adiabatic exponent (γ) of this gas.
View SolutionThe relation between U, P and V for an iodeal gas is U=2+3PV. What is the atomicity of the gas.
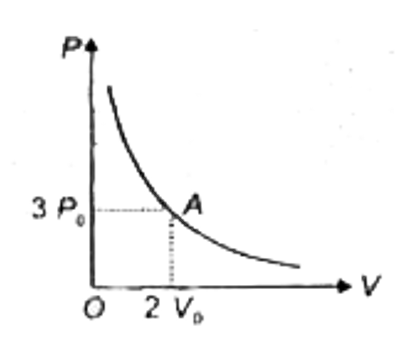
View SolutionThe variation of pressure P with volume V for an ideal monatomic gas during an adiabatic process is shown in figure . At point A the magnitude of rate of change of pressure with volume is
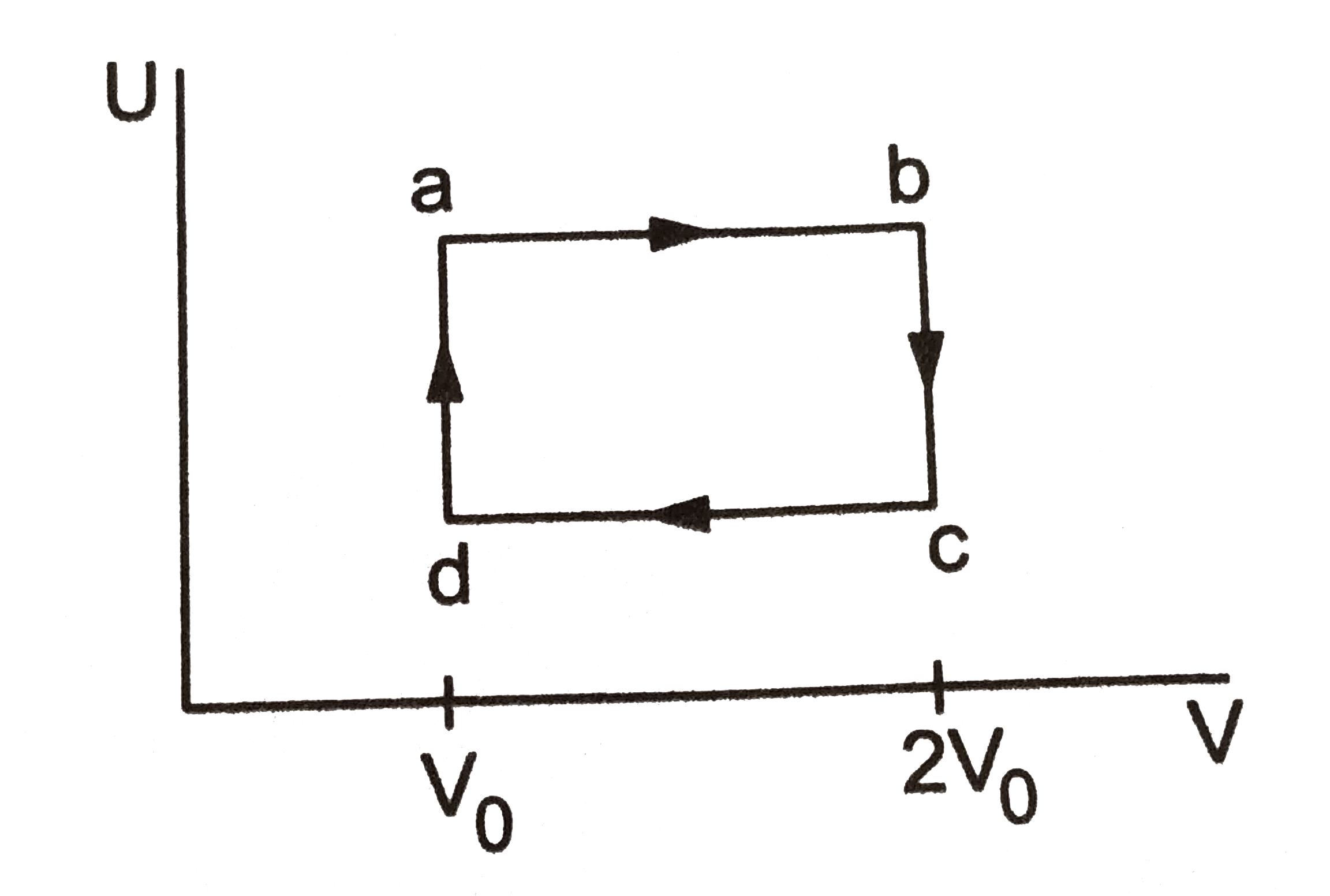
View SolutionFig shows the variation in the internal energy U with the volume V of 2.0 mol of an ideal gas in a cyclic process abcda. The temperatures of the gas at b and c are 500 K and 300 K respectively. Calculate the heat absorbed by the gas during the process.
View SolutionFigure. Shows three processes for an ideal gas. The temperature at 'a' is 600 K, pressure of 1 atm, and volume 1 L. The volume at 'b' is 4 L. Out of two processes, ab and ac, one is adiabatic and other is isothermal. The ratio of specific heats of the gas is 1.5.
a. Which of the processes ab and ac is adiabatic ? Why
b. Compute the pressure of the gas at b and c.
c. Compute the temperature at b and c.
d. Complete the volume at c.

View SolutionThe internal energy of a gas is given by U=2pV. It expands from V0 to 2V0 against a constant pressure p0. The heat absorbed by the gas in the process is
View SolutionThe internal energy of a gas is given by U=2pV. It expands from V0 to 2V0 against a constant pressure p0. The heat absorbed by the gas in the process is
View Solution
