A brass disc fits in a hole in a steel plate. Would you heat or cool the system to loosen the disc form the hole? Assume that αs<αb.
First heated in cooled
First cooled then heated
Is heated
Is cooled
The correct Answer is:D
Coefficient of linear expansion of brass is greater than of steel 1.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0282videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0310videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES83videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
A brass disc fits snugly in a hole in a steel plate. Should you heat or cool the system to loosen the disc from the hole ? given that αb>αFe.
View SolutionA brass disc fits snugly in a hole in a steel plate. Should you heat or cool this system to losen the disc from the hole ? given that αb>αFe.
View SolutionA bimetallic strip is formed out of two identical strips one of copper and the other of brass. The co-efficients of linear expansion of the two metals are αC and αB. On heating, the temperature of the strip goes up by △T the strip bends to form an are of radius of curvature R. Then R is
View SolutionWe have a disc of neglligible thickness and whose surface mass density varies as radial distance from centre as σ=σ0(1+rR), where R is the radius of the disc. Specific heat of the material of the disc isC.
Disc is given an angular velocity ω0 and placed on a horizontal rough surface such that the plane of the disc is parallel to the surface. Coefficient of friction between disc and suface is μ. The temperature of the disc is T0.
Answer the following question on the base of information provided in the above paragraph
If the kinetic energy lost due to the friction between disc and surface is absorbed by the disc the moment heat is generated, by the mass lying at the point where the energy is lost. Assume that there is no radial heat flow in betwen disc particles. Rate of change in temperature at a point lying at r distance away from centre with time, before disc stops rotating, will be (α-magnitude of angular acceleration of rod)View SolutionA cylindrical steel plug is inserted into a circular hole of diameter 2.60 cm in a brass plate. When the plug and the plates are at a temperature of 20∘C, the diameter of the plug is 0.010 cm smaller than that of the hole. The temperature at which the plug will just fit in it is
(Given,αsteel=11×10−6C−1andαbrass=19×10−6C−1View Solutiona large steel wheel is to be fitted on to a shaft of the same material. At 27∘C, the outer diameter of the shaft is 8.70cm and the diameter of the central hole in the wheel is 8.69cm . The shaft is cooled using 'dry ice' , At what temperature of the shaft does the wheel slip on the shaft? Assume coefficient of linear expansion of the steel to be constant over the required temperature range: αsteel=1.20×10−5K−1.
View SolutionA disc of mass m and radius R is attached to a rectangular plate of the same mass m, breadth R and length 2R as shown in figure. The moment of inertia of the system about the axis AB passing through the centre of the disc and along the plane is I=1α(313mR2).
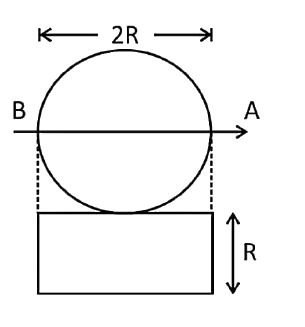View SolutionA disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.
View SolutionThere is a thin uniform disc of radius R and mass per unit area σ in which a hole of radius R/2 has been cut out as shown in the figure. Inside the hole, a square plate of same mass per unit area σ is inserted so that its corners touch the periphery of the hole. The distance of the centre of mass of the system from the origin is
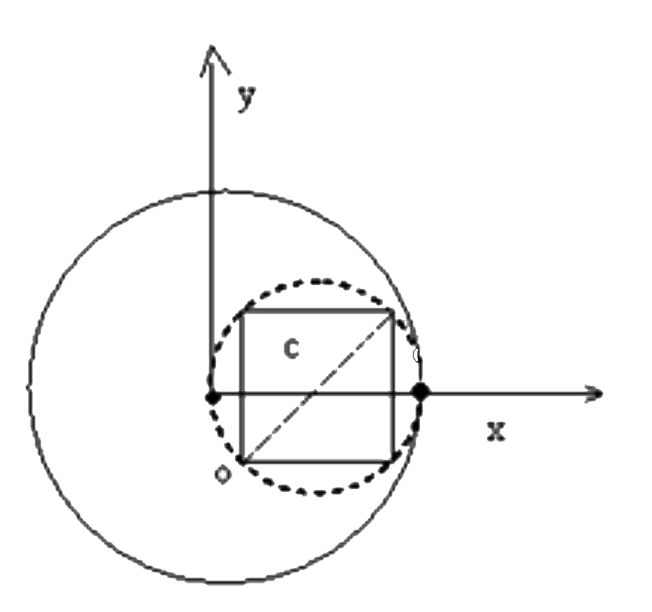View SolutionA fine steel wire of length 4m is fixed rigidly in a heavy brass frame as ashown in figure . It is just taut at 20∘C. The tensile stress developed in steel wire it whole system is heated to 120∘C is :-
(Givenαbrass=1.8×10−5.∘C−1,αsteel=1.2×10−5.∘C,
Ysteel=2×1011Nm−2,Ybrass=1.7×107Nm−2)
_S01_081_Q01.png)
View Solution