A brass disc fits snugly in a hole in a steel plate. Should you heat or cool this system to losen the disc from the hole ? given that αb>αFe.
The correct Answer is:We will cool the system
To determine whether to heat or cool a system consisting of a brass disc snugly fitting in a hole in a steel plate, we need to consider the coefficients of linear expansion for both materials.
1. Understand the Coefficients of Linear Expansion:
- The coefficient of linear expansion (α) indicates how much a material expands or contracts per degree change in temperature.
- In this case, we are given that the coefficient of linear expansion for brass (α_b) is greater than that for steel (α_Fe).
2. Analyze the Effect of Temperature Change:
- When the temperature of a material increases, it expands. Conversely, when the temperature decreases, it contracts.
- Since α_b > α_Fe, this means that brass will expand more than steel when heated and contract more than steel when cooled.
3. Determine the Action to Take:
- To loosen the brass disc from the steel plate, we want the disc to become smaller relative to the hole in the plate.
- If we cool the system, the brass disc will contract more than the steel plate due to its higher coefficient of linear expansion. This will create more space for the disc, allowing it to loosen from the hole.
4. Conclusion:
- Therefore, to loosen the brass disc from the hole in the steel plate, we should cool the system.
Final Answer:
We should cool the system to loosen the disc from the hole.
---
- The coefficient of linear expansion (α) indicates how much a material expands or contracts per degree change in temperature.
- In this case, we are given that the coefficient of linear expansion for brass (α_b) is greater than that for steel (α_Fe).
- When the temperature of a material increases, it expands. Conversely, when the temperature decreases, it contracts.
- Since α_b > α_Fe, this means that brass will expand more than steel when heated and contract more than steel when cooled.
- To loosen the brass disc from the steel plate, we want the disc to become smaller relative to the hole in the plate.
- If we cool the system, the brass disc will contract more than the steel plate due to its higher coefficient of linear expansion. This will create more space for the disc, allowing it to loosen from the hole.
- Therefore, to loosen the brass disc from the hole in the steel plate, we should cool the system.
We should cool the system to loosen the disc from the hole.
Topper's Solved these Questions
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercise-2
1 Videos
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercie-3
1 Videos
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercise-1
1 Videos
- CALORIMETRYBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise
19 Videos
- CAPACITORBOOK - RESONANCE ENGLISHCHAPTER - CAPACITOREXERCISE - Exercise
45 Videos
Similar Questions
A brass disc fits snugly in a hole in a steel plate. Should you heat or cool the system to loosen the disc from the hole ? given that αb>αFe.
View Solution
In the accompanying figure. Line l passes through the origin and the point (2, 4). Line m (not shown) is perpendicular to line l at (2, 4). Line m intersects the x-axis at which point?
View SolutionA uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View SolutionA disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.

View SolutionA small coin of mass 40 g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2 rad s−2. The coefficient of static friction between the coin and the disc is μs=3/4 and the coefficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is?

View SolutionA small coin of mass 80g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2rad/s2. The coefficient of static friction between the coin and the disc is μs=3/4 and cofficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is

View SolutionA small coin of mass 80g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2rad/s2. The coefficient of static friction between the coin and the disc is μs=3/4 and cofficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is

View SolutionA circular hole of radius R/2 is cut from a circular disc of radius R. The disc lies in the xy-plane and its centre coincides with the origin. If the remaining mass of the disc is M, then
a. determine the initial mass of the disc and
b. determine its moment of inertia about the z-axis.
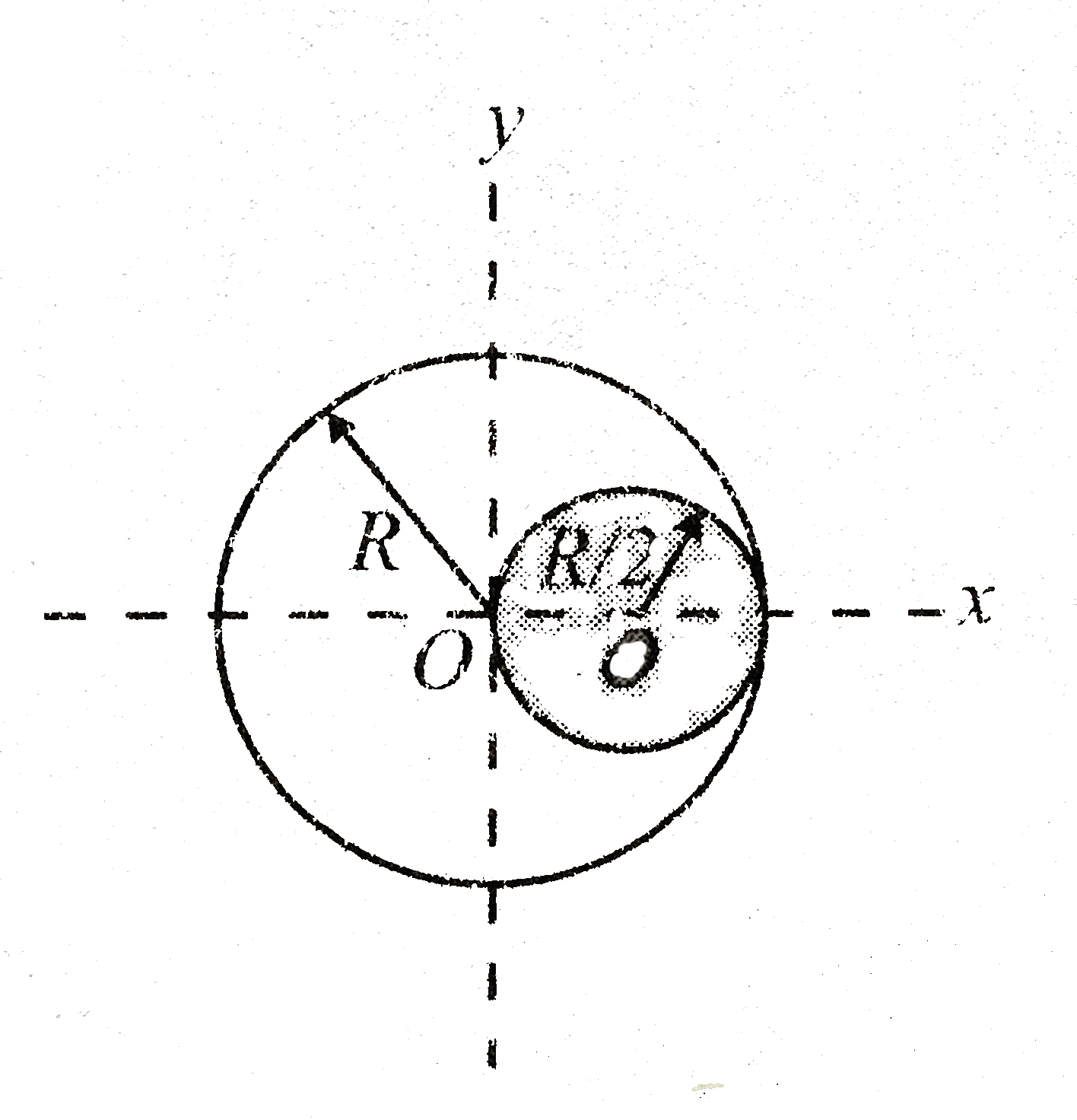
View SolutionFind the position of center of mass of the uniform lamina shown in figure, if small disc of radius α2 is cut from disc of radius a.
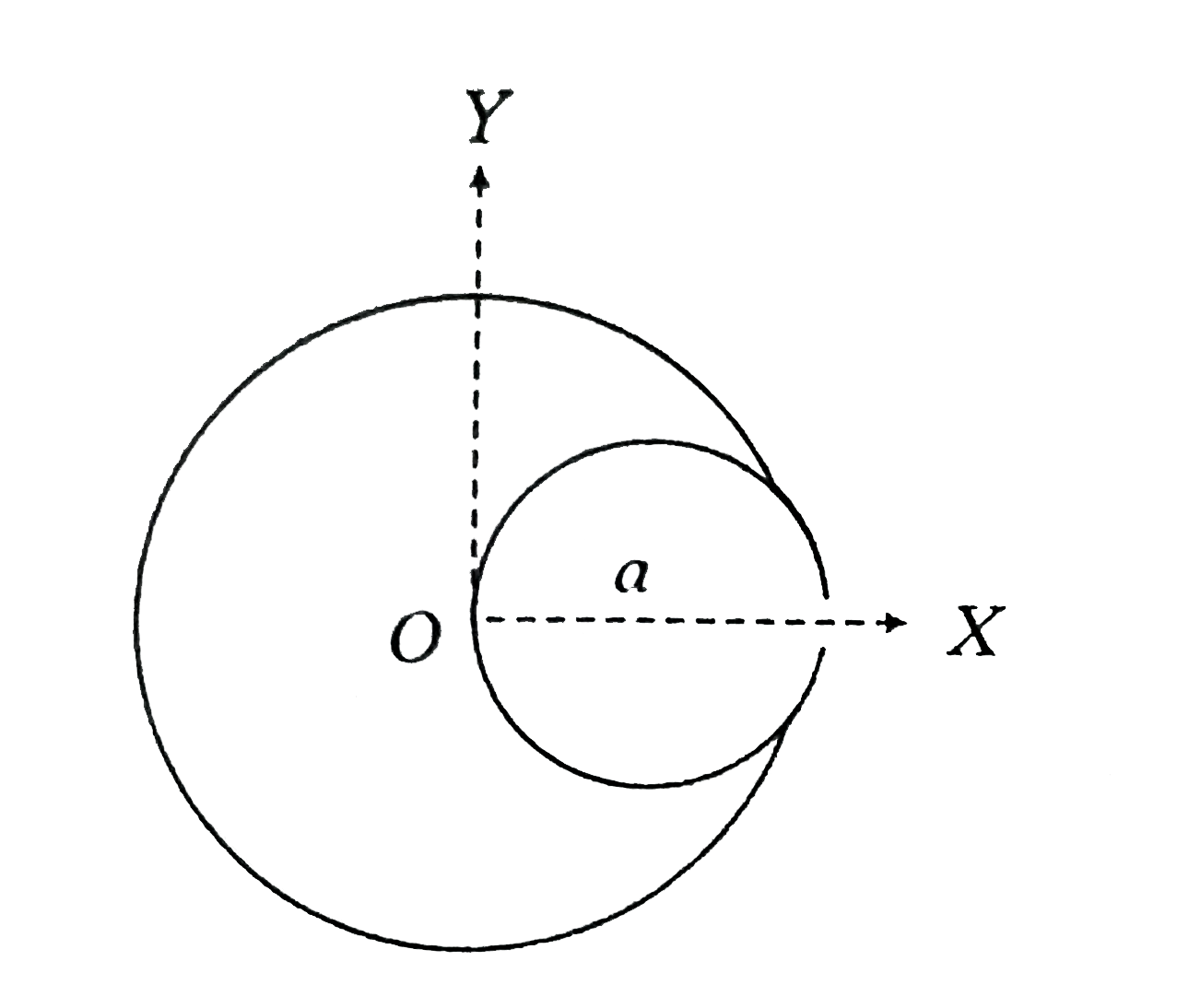
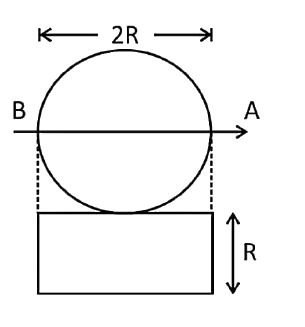
View SolutionA disc of mass m and radius R is attached to a rectangular plate of the same mass m, breadth R and length 2R as shown in figure. The moment of inertia of the system about the axis AB passing through the centre of the disc and along the plane is I=1α(313mR2).
View Solution
