The figure shows the face and interface temperature of a composite slab containing of four layers of two materials having identical thickness. Under steady state condition, find the value of temperature θ. _E01_247_Q01.png)
The correct Answer is:5∘C
ΔQΔt=same SoKA(20−10)l=2KA(10−0)l⇒2θ=10⇒θ=5∘C
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)15videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (A)73videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - Comprehension Based Questions66videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
The temperature of the two outer surfaces of a composite slab consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab in steady state is (AK(T2−T1)x)f. where, f is equal to
.View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T2 and T1(T2>T1). The rate of heat of heat transfer through the slab, in ? steady state is [(AT2−T1x]f, with f equal to :-
View Solution
Knowledge Check
- Question 1 - Select One
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
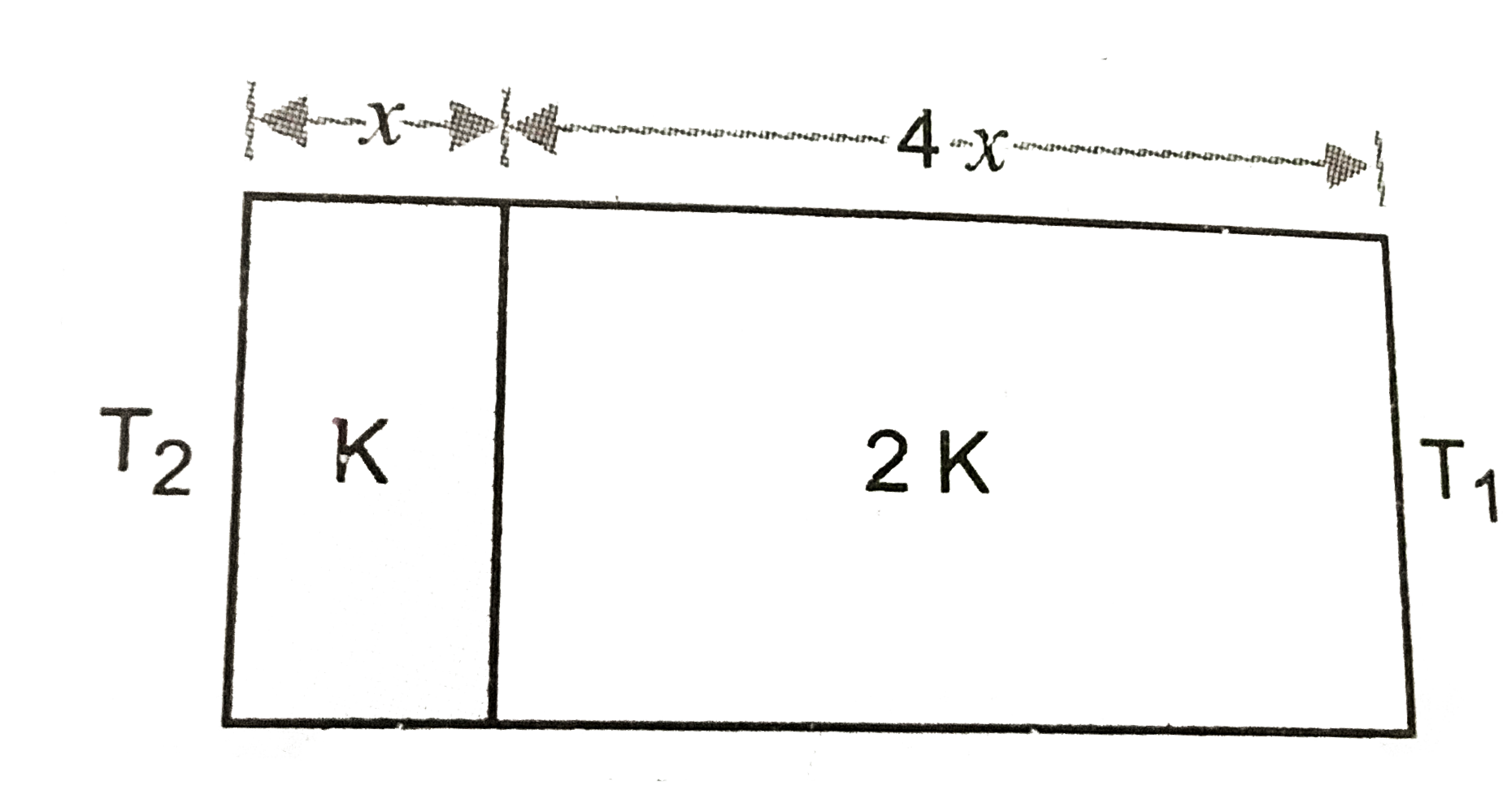A1B12C23D13
Figure shows a large tank of water at a constant temperature θ0 and a small vessel containing a mass m of water at an initial temperature θ1(<θ0). A metal rod of length L, area of cross section A and thermal conductivity K connects the two vessels. Find the time taken for the temperature of the water in the smaller vessel to become θ2(θ1<θ2<θ0) . Specific heat capacity of water is s and all other heat capacities are negligible.
View SolutionA slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate
The final temperatureView SolutionFigure shows in cross section a wall consisting of four layers with thermal conductivities K1=0.06W/mK,K3=0.04W/mKandK4=0.10W/mK. The layer thickness are L1=1.5cm,L3=2.8cmandL4=3.5cm. The temperature of interfaces is as shown in figure. energy transfer through the wall is in steady state. the temperature of the interface between layer 3and4 is:
View SolutionFigure shows in cross section a wall consisting of four layers with thermal conductivities K1=0.06W/mK,K3=0.04W/mKandK4=0.10W/mK. The layer thickness are L1=1.5cm,L3=2.8cmandL4=3.5cm. The temperature of interfaces is as shown in figure. energy transfer through the wall is in steady state. the temperature of the interface between layer 3and4 is:
View Solution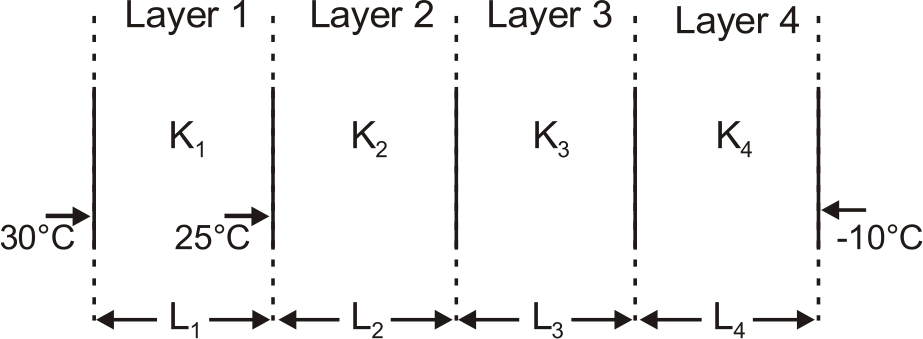
Figure shows in cros section a wall consisting of four layers with thermal conductivities K1=0.06W/mK
K3=0.04W/mK and K4=0.10W/mK. The layer thicknesses are L1=1.5cm,L3=2.8 cm and L4=3.5cm the temperature of interfaces is as shown in figure. energy transfer through the wall is in steady state.
Q. The temperature of the inteface between layers 2 and 3 isView SolutionTwo walls of thickness in the ratio 1:3 and thermal conductivities in the ratio 3:2 form a composite wall of a building. If the free surfaces of the wall be at temperatures 30∘C and 20∘C, respectively, what is the temperature of the interface?
View Solution