P-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
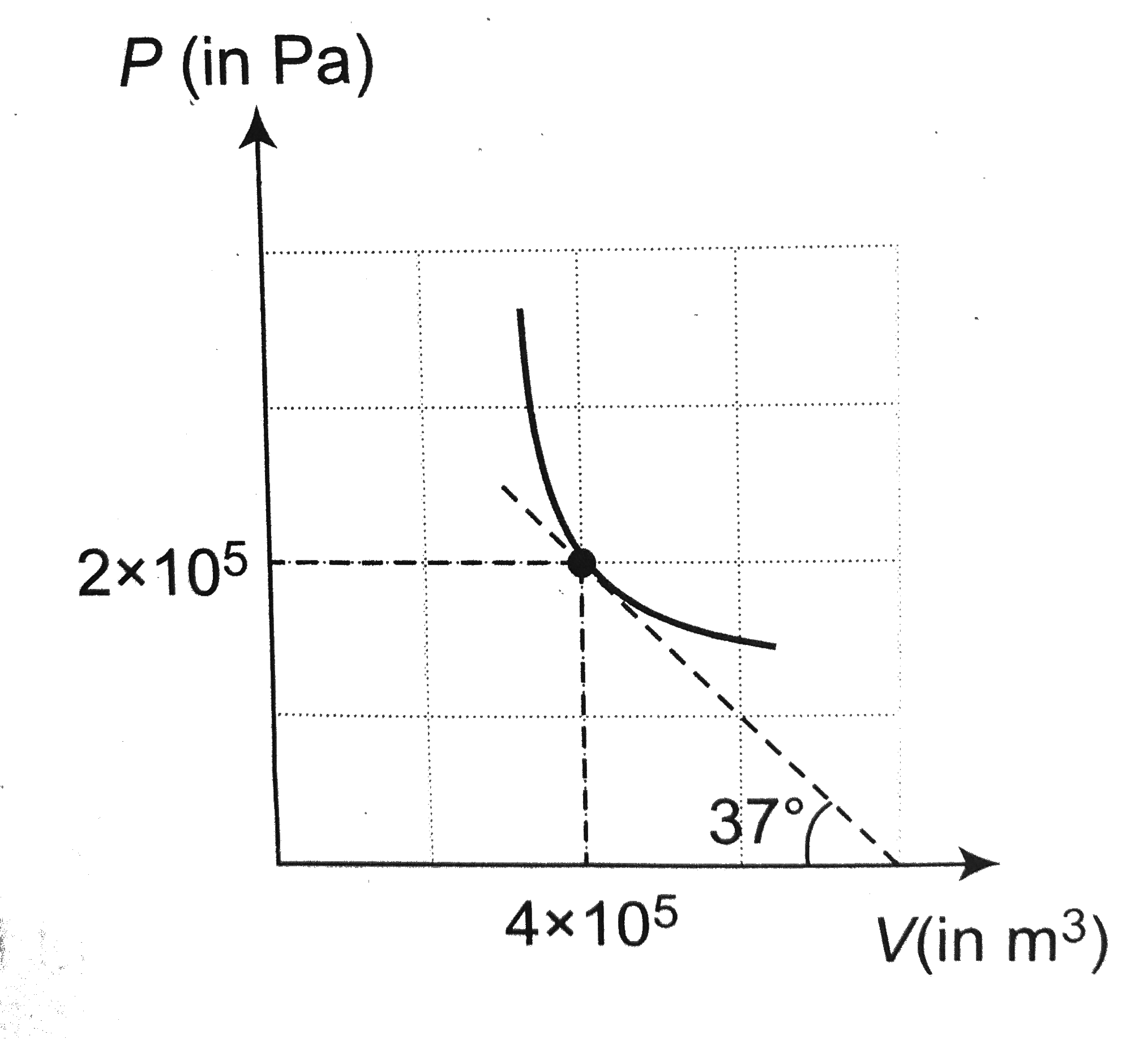
The correct Answer is:1.5
Slope = −γPV=−tan37∘⇒mPV=tan37∘
⇒m=(VP)(34)=(4×1052×105)(34)=32=1.5
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)
15 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (A)
73 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - Comprehension Based Questions
66 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
An ideal monatomic gas undergoes process PV1.25 = constant .Then
View SolutionA certain ideal gas undergoes a polytropic process PVn = constant such that the molar specific heat during the process is negative. If the ratio of the specific heats of the gas be γ, then the range of values of n will be
View SolutionA certain ideal gas undergoes a polytropic process PVn = constant such that the molar specific heat during the process is negative. If the ratio of the specific heats of the gas be γ, then the range of values of n will be
View Solution1 mole of an ideal diatomic gas undergoes a reversible polytropic process (PV2=constant). The gas expand from initial volume of 1 litre and temp 300K to final volume 3 lit. Claculate change in internal energy (approx).
View SolutionA cyclic process ABCD is shown in the P−V diagram. Which of the following curves represents the same process?

View SolutionOne mole of an ideal gas is taken along the process in which PVx=constant. The graph shown represents the variation of molar heat capacity of such a gas with respect to x. The values of c’ and x’. respectively, are given by
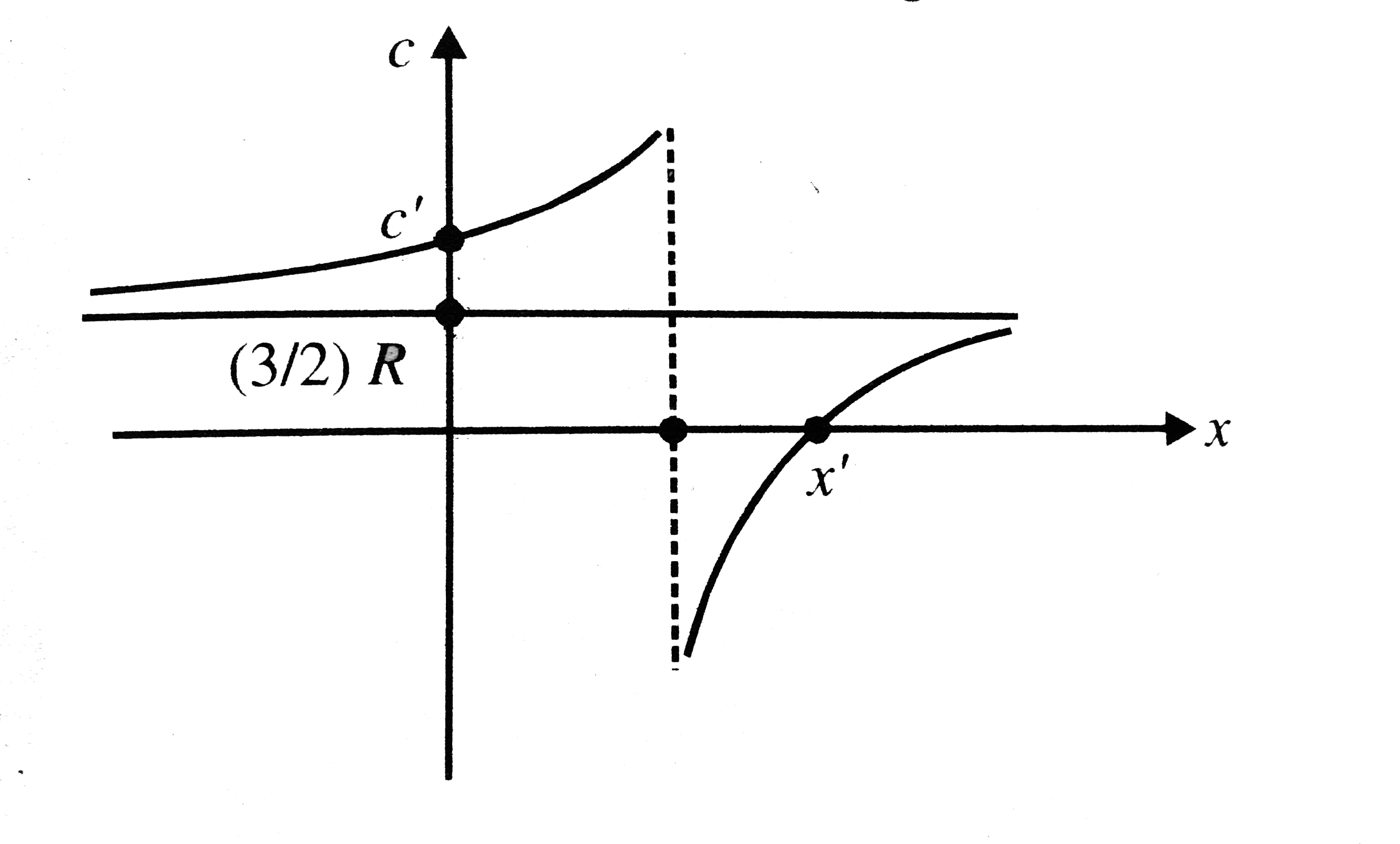
View SolutionOne mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
View SolutionFor polytropic process PVn = constant, molar heat capacity (Cm) of an ideal gas is given by:
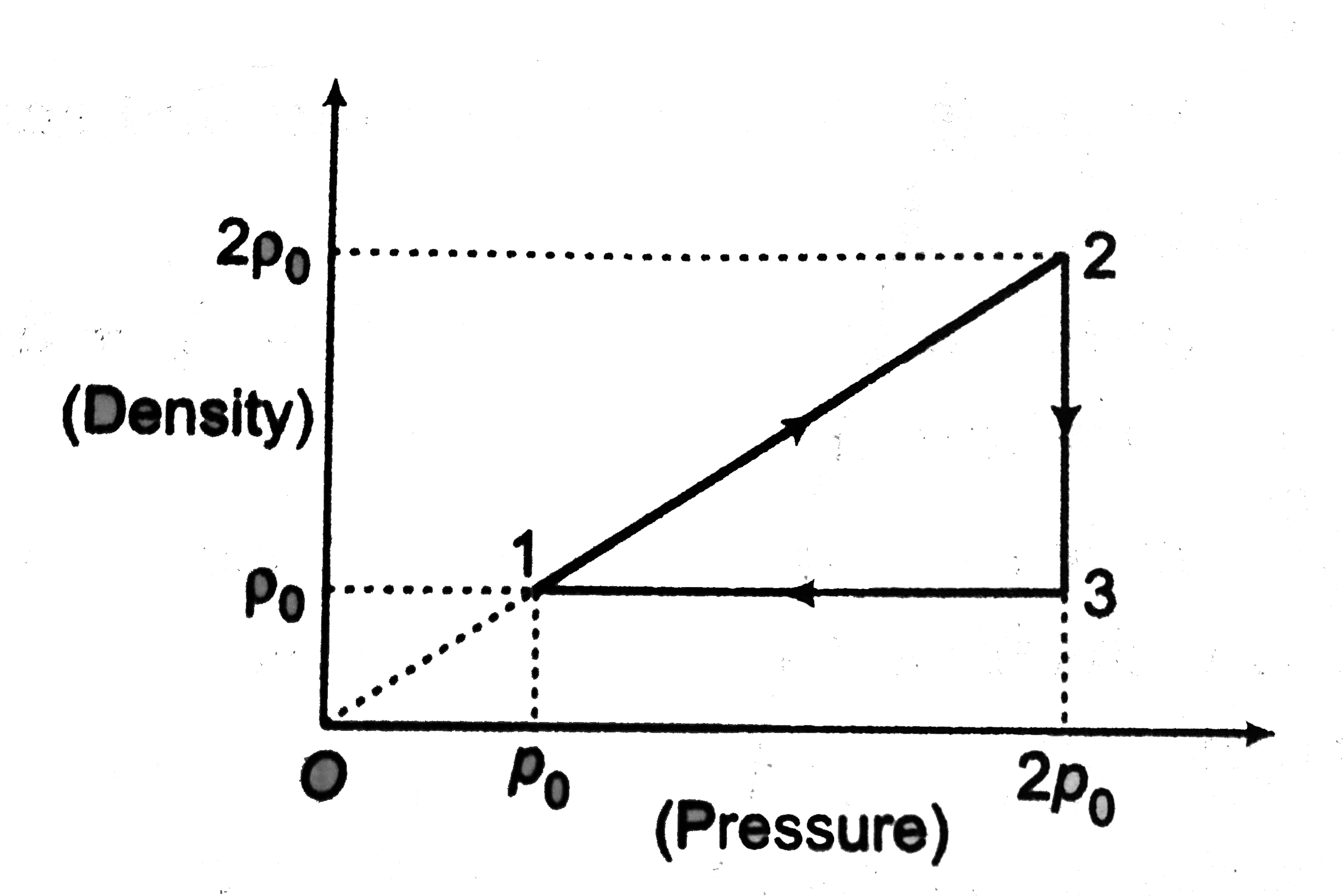
View SolutionThe density (ρ) versus pressure (p) graph of one mole of an ideal monoatomic gas undergoing a cyclic process is shown in figure. Molecular mass of gas is M.
(a) Find work done in each process.
(b) Find heat rejected by gas in one complete cycle.
(c) Find the efficiency of the cycle.
View SolutionA process in which work perfomed by an ideal gas is proportional to the corresponding increment of its internal energy is described as a polytropic process. If we represent work done by a ppolytropic process by W and increase in internal energy as ΔU then
W∝ΔU
or W=K1ΔU ...(i)
For this process, it can be demonstrated that the relation between pressure and volume is given by the equation
PVη=K2 (constant ) .....(ii)
We know that a gas can have various values for molar specific heats. The molar specific heat 'C' for an ideal gas in polytropic process can be calculated with the help of first law of thermodynamics. In polytropic process process the variation of molar specific heat 'C' with η for a monatomic gas is plotted as in the graph shown.

For a monoatomic gas, the values of polytropic constant η for which value specific heat is negative.
View Solution
