A certain ideal gas undergoes a polytropic process PVn = constant such that the molar specific heat during the process is negative. If the ratio of the specific heats of the gas be γ, then the range of values of n will be
0<n<γ
1<n<γ
n=γ
n>γ
The correct Answer is:B
To solve the problem, we need to determine the range of values for the polytropic index n under the condition that the molar specific heat during the process is negative.
1. Understanding Polytropic Process:
A polytropic process is defined by the equation PVn=constant. The specific heat during this process can be expressed in terms of the change in internal energy and work done.
2. First Law of Thermodynamics:
The first law states that:
dQ=dU+dW
where dQ is the heat added to the system, dU is the change in internal energy, and dW is the work done by the system.
3. Specific Heat Definition:
The molar specific heat C for a process can be defined as:
C=dQdT
where dT is the change in temperature.
4. Work Done in a Polytropic Process:
The work done dW in a polytropic process can be expressed as:
dW=nRdT/(1−n)
where R is the gas constant.
5. Change in Internal Energy:
The change in internal energy dU can be expressed as:
dU=F2NRdT
where F is the degrees of freedom of the gas.
6. Combining the Equations:
From the first law, we can substitute for dQ:
dQ=dU+dW=F2NRdT+nRdT1−n
7. Finding Molar Specific Heat:
Dividing by NdT gives:
C=F2R+nRN(1−n)
8. Condition for Negative Specific Heat:
For the specific heat C to be negative, we require:
F2R+nR1−n<0
Simplifying, we find:
F2+n1−n<0
9. Rearranging the Inequality:
Rearranging gives:
n1−n<−F2
This implies:
n<−F2(1−n)
10. Finding the Range of n:
Solving this inequality leads to:
n>1
Thus, the range of n is:
n>1
Conclusion:
The range of values for n in the polytropic process where the molar specific heat is negative is:
n>1
A polytropic process is defined by the equation PVn=constant. The specific heat during this process can be expressed in terms of the change in internal energy and work done.
The first law states that:
dQ=dU+dW
where dQ is the heat added to the system, dU is the change in internal energy, and dW is the work done by the system.
The molar specific heat C for a process can be defined as:
C=dQdT
where dT is the change in temperature.
The work done dW in a polytropic process can be expressed as:
dW=nRdT/(1−n)
where R is the gas constant.
The change in internal energy dU can be expressed as:
dU=F2NRdT
where F is the degrees of freedom of the gas.
From the first law, we can substitute for dQ:
dQ=dU+dW=F2NRdT+nRdT1−n
Dividing by NdT gives:
C=F2R+nRN(1−n)
For the specific heat C to be negative, we require:
F2R+nR1−n<0
Simplifying, we find:
F2+n1−n<0
Rearranging gives:
n1−n<−F2
This implies:
n<−F2(1−n)
Solving this inequality leads to:
n>1
Thus, the range of n is:
n>1
The range of values for n in the polytropic process where the molar specific heat is negative is:
n>1
Similar Questions
Knowledge Check
If a gas has n degrees of freedom ratio of specific heats of gas is
A1+n2B1+1nC1+n2D1+2nThe specific heat of a gas in an isothermal process is
AinfiniteBzeroCnegativeDremains constant
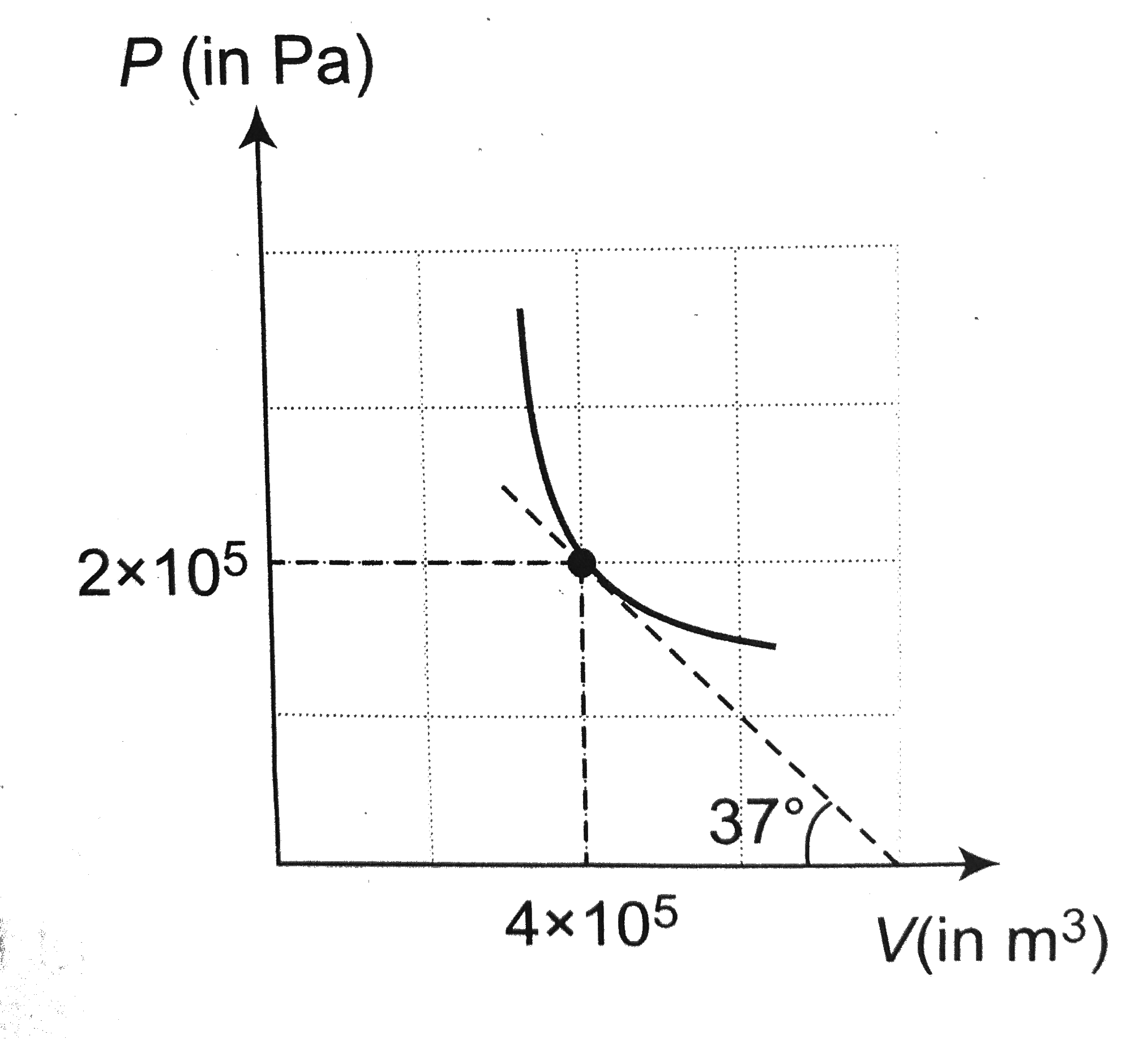
P-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
View SolutionA certain amount of ideal monoatomic gas undergoes a process given by TV1/2= constant. The molar specific heat of the gas for the process will be given by
View Solutionan ideal diatomic gas undergoes a polytropic process described by the equation P√V=constant . The molar heat capacity of the gas during this process is
View SolutionThe specific heat of an ideal gas varies with temperature T as
View SolutionFor a certain gas the ratio of specific heats is given to be γ=1.5, for this gas
View SolutionFor a gas, molar specific heat in a process is greater then CV . Which of the following relation is possible?
View Solution
