One end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of lengths l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two sections is
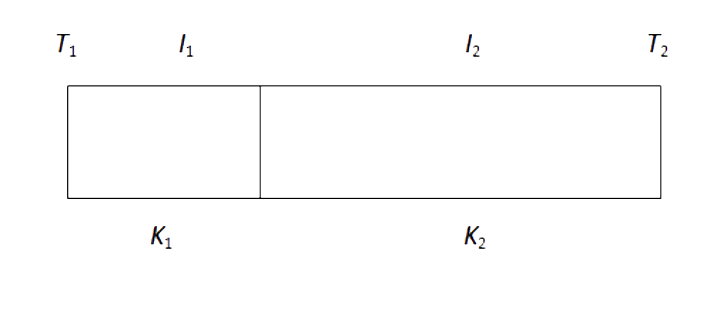
(K2l2T1+K1l1T2)/(K1l1+K2l2)
(K2l1T1+K1l2T2)/(K2l1+K1l2)
(K1l2T1+K2l1T2)/(K1l2+K2l1)
(K1l1T1+K2l2T2)/(K1l1+K2l2)
The correct Answer is:C
Let the temperature of the interface be T0.
Thermal current =Temperature differenceThermal resitance
Thermal resistance = 1KlA
⇒T1−T0l1/K1A=T0−T2l2/K2A
⇒T0=K1l2T1−K2l1T2K1l2+K2l1
_E01_317_S01.png)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B)58videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B) (MCQ)9videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)15videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
One end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
View SolutionOne end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
View Solution
Knowledge Check
- Question 1 - Select One
Two rods of length l1andl2 and coefficients of thermal conductivities k1andK2 are kept touching each other. Both have the same area of cross-section. The equivalent of thermal conductivity is
AK1+K2BK1l1+K2l2CK1l1+K2l2l1+l2Dl1+l2(l1/K1)+(l2/K2) - Question 2 - Select One
Two walls of thickness d1andd2 and thermal conductivites K1andK2 are in contact. In the steady state, if the temperature at the outer surfaces are T1andT2 the temperature at the common wall is
AK1T1d2+K2T2d1K1d2+K2d1BK1T1+K2T2d2+d1C(K1d1+K2d2T1+T2)T1T2DK1T1d1+K2T2d2K1d1+K2d2
One end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
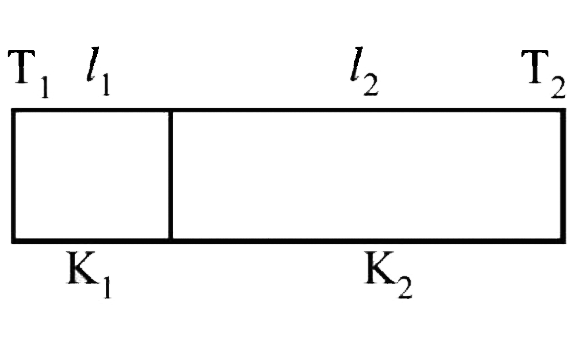 View Solution
View SolutionTwo rods A and B are of equal lengths. Their ends of kept between the same temperature and their area of cross-section are A1 and A2 and thermal conductivities K1 and K2. The rate of heat transmission in the two rods will be equal, if
View SolutionA composite slab is prepared by pasting two plates of thickness L1 and L2 and thermal conductivities K1 and K2 . The slab have equal cross-sectional area. Find the equivalent conductivity of the composite slab.
View SolutionTwo conducting cylinders of equal length but different radii are connected in series between two heat baths kept at temperatures T1=300KandT2=100K, as shown in the figure. The radius of the bigger cylinder is twice that of the smaller one and the thermal conductivities of the materials of the smaller and the larger cylinders are K1andK2 respectively. If the temperature at the junction of the two cylinders in the steady state is 200 K, then K1/K2=__________.
View SolutionTwo rods of length d1 and d2 and coefficients of thermal conductivites K1 and K2 are kept touching each other. Both have the same area of cross-section. The equivalent thermal conductivity.
View SolutionOne end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.
 View Solution
View Solution
