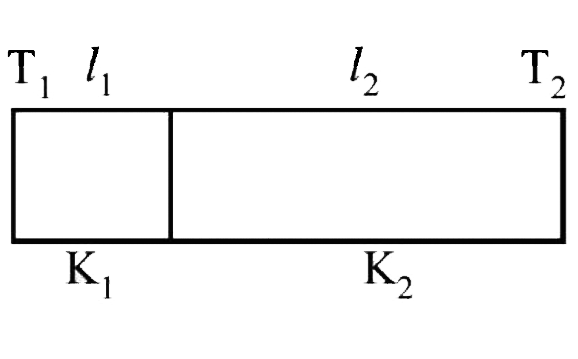
One end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
(k1l1T1+K2l2T2)(K1l1+K2l2)
(K2l2T1+K1l1T2)(K1l1+K2l2)
(K2l1T1+K1l2T2)(K2l2+K1l2)
(K1l2T1+K2l2T2)(K1l2+K2l1)
The correct Answer is:D
To find the temperature at the interface of the two sections of the thermally insulated rod, we can follow these steps:
1. Identify the Setup:
- We have a rod divided into two sections.
- The left section has length l1 and thermal conductivity k1.
- The right section has length l2 and thermal conductivity k2.
- The temperatures at the ends of the rod are T1 (at the left end) and T2 (at the right end).
2. Understand Heat Flow:
- Heat flows from the hotter end T1 to the cooler end T2.
- Let T0 be the temperature at the interface between the two sections.
3. Apply Fourier's Law of Heat Conduction:
- The rate of heat flow (heat current) through each section must be equal at steady state.
- For section 1 (length l1):
Q1=k1A(T1−T0)l1
- For section 2 (length l2):
Q2=k2A(T0−T2)l2
4. Set the Heat Currents Equal:
- Since Q1=Q2:
k1A(T1−T0)l1=k2A(T0−T2)l2
- The area A cancels out from both sides.
5. Rearrange the Equation:
- Cross-multiply to eliminate the fractions:
k1(T1−T0)l2=k2(T0−T2)l1
- Expand both sides:
k1T1l2−k1T0l2=k2T0l1−k2T2l1
6. Collect Terms Involving T0:
- Rearranging gives:
k1T1l2+k2T2l1=T0(k1l2+k2l1)
7. Solve for T0:
- Isolate T0:
T0=k1T1l2+k2T2l1k1l2+k2l1
Final Result:
The temperature at the interface T0 is given by:
T0=k1T1l2+k2T2l1k1l2+k2l1
- We have a rod divided into two sections.
- The left section has length l1 and thermal conductivity k1.
- The right section has length l2 and thermal conductivity k2.
- The temperatures at the ends of the rod are T1 (at the left end) and T2 (at the right end).
- Heat flows from the hotter end T1 to the cooler end T2.
- Let T0 be the temperature at the interface between the two sections.
- The rate of heat flow (heat current) through each section must be equal at steady state.
- For section 1 (length l1):
Q1=k1A(T1−T0)l1
- For section 2 (length l2):
Q2=k2A(T0−T2)l2
- Since Q1=Q2:
k1A(T1−T0)l1=k2A(T0−T2)l2
- The area A cancels out from both sides.
- Cross-multiply to eliminate the fractions:
k1(T1−T0)l2=k2(T0−T2)l1
- Expand both sides:
k1T1l2−k1T0l2=k2T0l1−k2T2l1
- Rearranging gives:
k1T1l2+k2T2l1=T0(k1l2+k2l1)
- Isolate T0:
T0=k1T1l2+k2T2l1k1l2+k2l1
The temperature at the interface T0 is given by:
T0=k1T1l2+k2T2l1k1l2+k2l1
Similar Questions
One end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
View SolutionTwo rods A and B are of equal lengths. Their ends of kept between the same temperature and their area of cross-section are A1 and A2 and thermal conductivities K1 and K2. The rate of heat transmission in the two rods will be equal, if
View Solution
Knowledge Check
Two rods of length l1andl2 and coefficients of thermal conductivities k1andK2 are kept touching each other. Both have the same area of cross-section. The equivalent of thermal conductivity is
AK1+K2BK1l1+K2l2CK1l1+K2l2l1+l2Dl1+l2(l1/K1)+(l2/K2)
Two conducting cylinders of equal length but different radii are connected in series between two heat baths kept at temperatures T1=300KandT2=100K, as shown in the figure. The radius of the bigger cylinder is twice that of the smaller one and the thermal conductivities of the materials of the smaller and the larger cylinders are K1andK2 respectively. If the temperature at the junction of the two cylinders in the steady state is 200 K, then K1/K2=__________.
View SolutionOne end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.

View SolutionOne end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
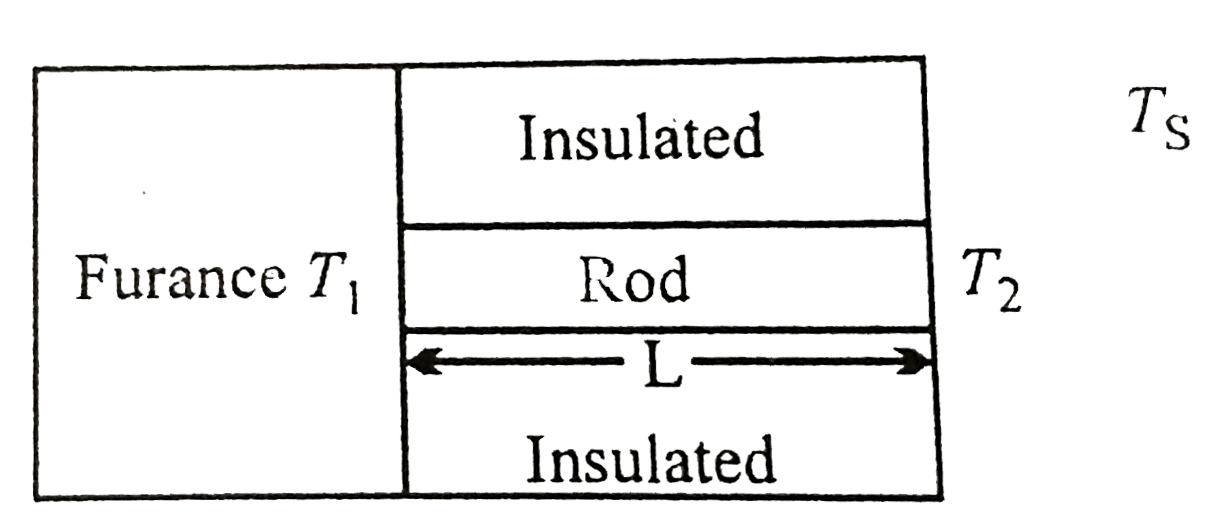
View SolutionA composite slab is prepared by pasting two plates of thickness L1 and L2 and thermal conductivities K1 and K2 . The slab have equal cross-sectional area. Find the equivalent conductivity of the composite slab.
View SolutionA slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
View SolutionTwo metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
View SolutionTwo metal rods 1 and 2 of the same length have same temperature difference between their ends. Their thermal conductivities are K1andK2 and cross-section areas A1andA2 respectively. What is the required condition for the same rate of heat conduction in them?
View Solution
