When two plane mirrors subtend an angle θ between them, then a ray of light incident parallel to one of them retraces its path afer n reflections such that nθ=c (where c is constant)
What is the angle of c?
π
π2
3π2
None of these
The correct Answer is:B
To solve the problem, we need to analyze the situation involving two plane mirrors that subtend an angle θ between them. A ray of light is incident parallel to one of the mirrors and retraces its path after n reflections such that nθ=c, where c is a constant. Our goal is to find the value of c.
1. Understanding the Geometry:
- We have two plane mirrors forming an angle θ.
- A ray of light is incident parallel to one of the mirrors.
2. Reflection of Light:
- When the ray hits the second mirror, it reflects off at the same angle it arrived at, which is determined by the angle θ between the mirrors.
- The ray will continue to reflect between the mirrors.
3. Condition for Retracing Path:
- For the ray to retrace its path, the total angle of deviation after n reflections must equal 360∘ or a multiple of it.
- Each reflection contributes an angle of θ to the deviation.
4. Total Angle of Deviation:
- After n reflections, the total deviation is nθ.
- For the ray to retrace its path, we need nθ=360∘k for some integer k.
5. Finding c:
- The problem states that nθ=c.
- We can set c=360∘k.
- The simplest case is when k=1, which gives c=360∘.
6. Conclusion:
- Therefore, the constant c is 360∘.
Final Answer:
The angle c is 360∘.
- We have two plane mirrors forming an angle θ.
- A ray of light is incident parallel to one of the mirrors.
- When the ray hits the second mirror, it reflects off at the same angle it arrived at, which is determined by the angle θ between the mirrors.
- The ray will continue to reflect between the mirrors.
- For the ray to retrace its path, the total angle of deviation after n reflections must equal 360∘ or a multiple of it.
- Each reflection contributes an angle of θ to the deviation.
- After n reflections, the total deviation is nθ.
- For the ray to retrace its path, we need nθ=360∘k for some integer k.
- The problem states that nθ=c.
- We can set c=360∘k.
- The simplest case is when k=1, which gives c=360∘.
- Therefore, the constant c is 360∘.
The angle c is 360∘.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (A)
47 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)
15 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
36 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
When two plane mirrors subtend an angle θ between them, then a ray of light incident parallel to one of them retraces its path afer n reflections such that nθ=c (where c is constant)
If the angle between mirrors is 60∘ . Then light ray retraces its path after n reflections where n is
View SolutionWhen two plane mirrors subtend an angle θ between them, then a ray of light incident parallel to one of them retraces its path afer n reflections such that nθ=c (where c is constant)
The graph between θ and n will
View SolutionTwo mirrors are inclined at angle θ as shown in figure. Light rays are incident parallel to one of mirrors. Light will start retracing its path after the reflection if

View SolutionWhen a plane mirror is rotated through an angle θ then the reflected ray turns through the angle 2θ then the size of the image
View SolutionTwo plans mirrors are inclined to each other at some angle .A ray of light incident at 30∘on one,after reflection form the other retraces its path .The angles between the mirrors is:
View SolutionA mirror is inclined at an angle of θ with the horizontal. If a ray light is incident at an angle θ as shown , then the angle made by reflected ray with the horizontal is
_E01_002_Q01.png)
View SolutionIn the shown figure, mirror is rotated by an angle theta. Find theta if
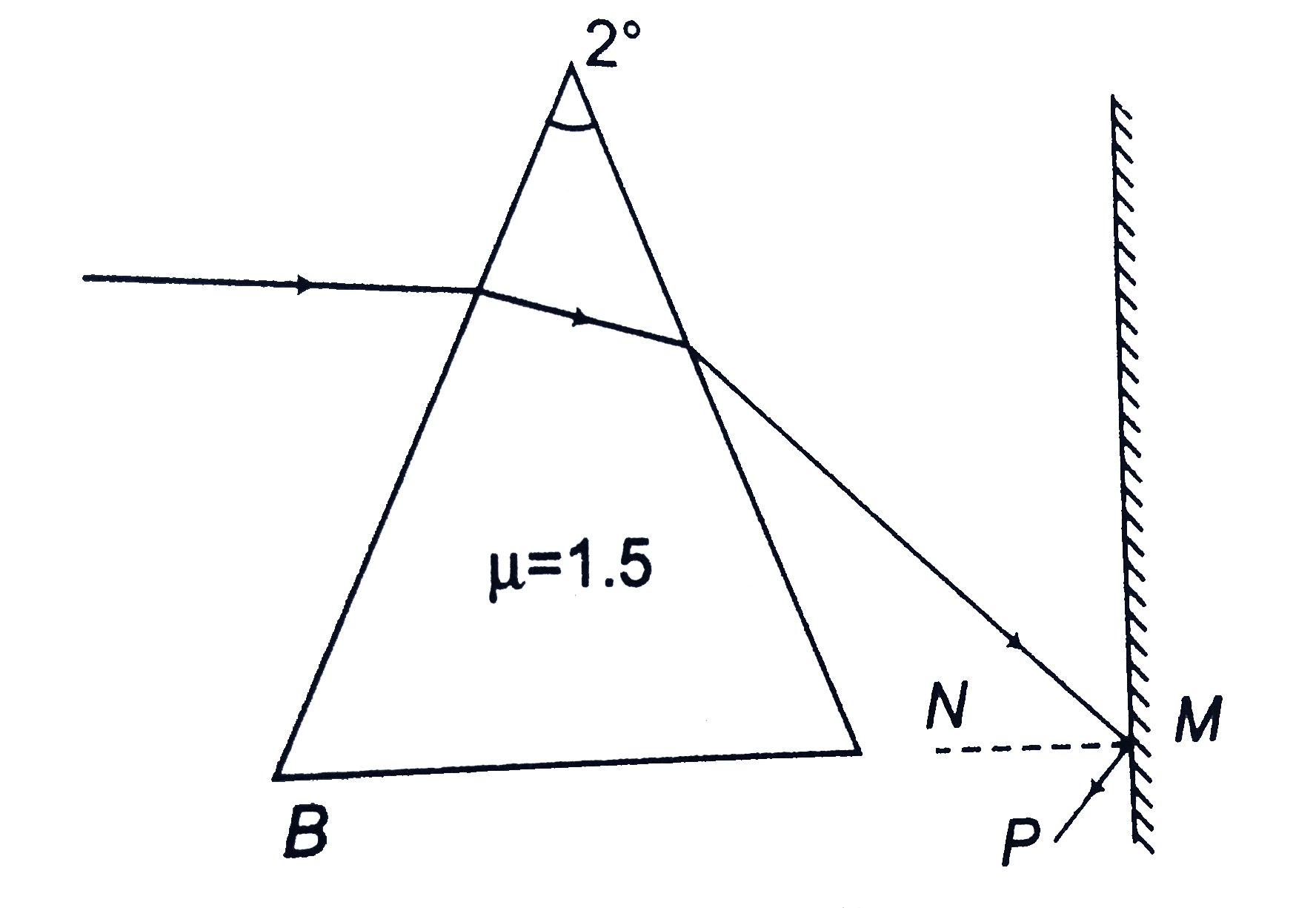
ray of light retraces its path after reflection from M
ray of light MP turns in the direction of MN.
View SolutionTwo plane mirrror are inclined to each other at 70∘. A ray of light is incident on one mirror. They ray after two reflections will undergo a total deviation of :
View SolutionTwo plane mirrors are inclined to each other at an angle 60∘ if a ray of light incident on first mirror parallel to the second mirror, it is reflected from the second mirror
View SolutionTwo plane mirrors are inclined to each other at an angle θ. A ray of light is reflected at one
mirror and then at the other. Find the total deviation of the ray.
View Solution
