When two plane mirrors subtend an angle between them, then a ray of light incident parallel to one of them retraces its path afer n reflections such that (where c is constant)
The graph between and n will
be continous but not differentiable
be continuous & differentiable
Not be continous
Can't say
The correct Answer is:C
To solve the problem, we need to analyze the relationship between the angle θ between two mirrors and the number of reflections n that a ray of light undergoes before retracing its path. The key relationship given is nθ=c, where c is a constant.
1. Understanding the Geometry:
- We have two plane mirrors that subtend an angle θ between them.
- A ray of light is incident parallel to one of the mirrors.
2. Analyzing Reflections:
- For n=1:
- The ray reflects off the first mirror and retraces its path, which requires θ=90∘ (since the ray must be parallel to the other mirror).
- For n=2:
- The ray reflects twice. However, there is no angle θ that allows the ray to retrace its path after two reflections. Thus, θ does not exist for n=2.
- For n=3:
- The ray reflects three times. The first reflection occurs at angle θ, the second reflection at angle 90∘−θ, and for the ray to retrace its path, the third reflection must also be at 90∘.
- This gives us the equation: 90−θ+θ+θ=180, leading to 2θ=90 or θ=45∘.
3. Finding a Pattern:
- Continuing this process, we can find values of θ for other odd values of n (like n=5,7, etc.) and notice that θ decreases as n increases.
- For even values of n, θ does not exist.
4. Graphing the Relationship:
- We can plot the values of θ against n:
- For n=1, θ=90∘.
- For n=2, no value exists.
- For n=3, θ=45∘.
- For n=4, no value exists.
- For n=5, we can find another value, and so forth.
- The graph will show points for odd n and gaps for even n.
5. Conclusion:
- The graph between θ and n will be discontinuous since there are values of n (even integers) for which θ does not exist.
Final Graph:
- The graph will consist of discrete points corresponding to odd values of n and will be discontinuous at even values of n.
- We have two plane mirrors that subtend an angle θ between them.
- A ray of light is incident parallel to one of the mirrors.
- For n=1:
- The ray reflects off the first mirror and retraces its path, which requires θ=90∘ (since the ray must be parallel to the other mirror).
- For n=2:
- The ray reflects twice. However, there is no angle θ that allows the ray to retrace its path after two reflections. Thus, θ does not exist for n=2.
- For n=3:
- The ray reflects three times. The first reflection occurs at angle θ, the second reflection at angle 90∘−θ, and for the ray to retrace its path, the third reflection must also be at 90∘.
- This gives us the equation: 90−θ+θ+θ=180, leading to 2θ=90 or θ=45∘.
- Continuing this process, we can find values of θ for other odd values of n (like n=5,7, etc.) and notice that θ decreases as n increases.
- For even values of n, θ does not exist.
- We can plot the values of θ against n:
- For n=1, θ=90∘.
- For n=2, no value exists.
- For n=3, θ=45∘.
- For n=4, no value exists.
- For n=5, we can find another value, and so forth.
- The graph will show points for odd n and gaps for even n.
- The graph between θ and n will be discontinuous since there are values of n (even integers) for which θ does not exist.
- The graph will consist of discrete points corresponding to odd values of n and will be discontinuous at even values of n.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (A)
47 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)
15 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
36 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
When two plane mirrors subtend an angle θ between them, then a ray of light incident parallel to one of them retraces its path afer n reflections such that nθ=c (where c is constant)
What is the angle of c?
View SolutionWhen two plane mirrors subtend an angle θ between them, then a ray of light incident parallel to one of them retraces its path afer n reflections such that nθ=c (where c is constant)
If the angle between mirrors is 60∘ . Then light ray retraces its path after n reflections where n is
View SolutionTwo mirrors are inclined at angle θ as shown in figure. Light rays are incident parallel to one of mirrors. Light will start retracing its path after the reflection if

View SolutionWhen the two plane mirror are parallel to each other, then the number of images of an object placed between them is
View SolutionTwo plans mirrors are inclined to each other at some angle .A ray of light incident at 30∘on one,after reflection form the other retraces its path .The angles between the mirrors is:
View SolutionIn the shown figure, mirror is rotated by an angle theta. Find theta if
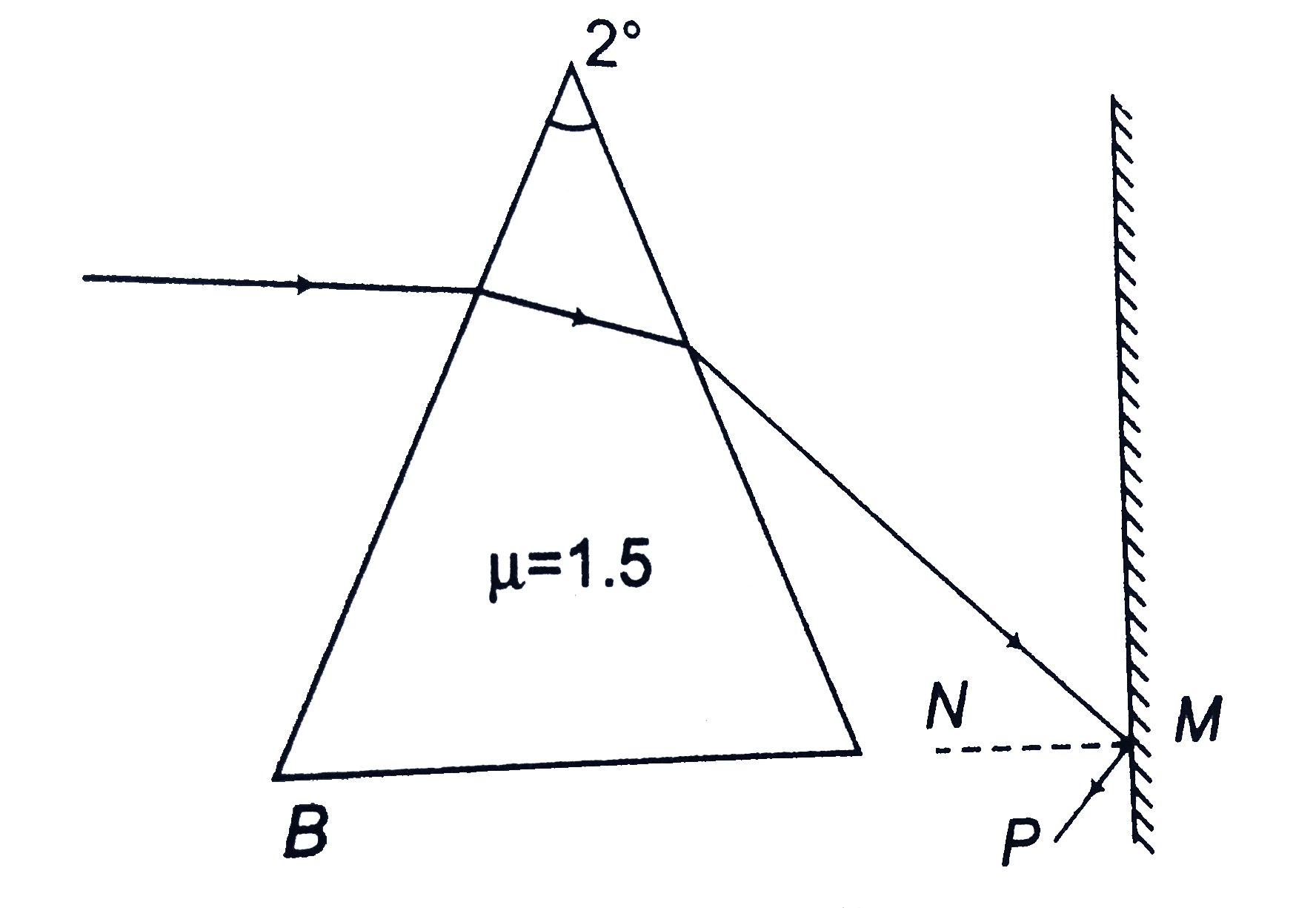
ray of light retraces its path after reflection from M
ray of light MP turns in the direction of MN.
View SolutionTwo plane mirrors are inclined to each other at an angle θ. A ray of light is reflected at one
mirror and then at the other. Find the total deviation of the ray.
View SolutionTwo plane mirrors are inclined to each other at an angle 60∘ if a ray of light incident on first mirror parallel to the second mirror, it is reflected from the second mirror
View SolutionTwo plane mirror M1 and M2 area inclined at angle θ as<br> shown. A ray of light 1, which is parallel to M1strikes M2 and after two
reflection , the ray 2 become parrallel to M2.Find the angle θ

View SolutionTwo plane mirror M1 and M2 area inclined at angle θ as<br> shown. A ray of light 1, which is parallel to M1strikes M2 and after two
reflection , the ray 2 become parrallel to M2.Find the angle θ

View Solution
