In the given figure the angle (in degree) between the velocity vector of object and image is α . The value of α10 is
_E01_163_Q01.png)
The correct Answer is:9
(→VOM)x=−(→VIM)x & (→VOM)y=−(→VIM)y
_E01_163_S01.png)
(→VI)x=−15m/s
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-05 (A)35videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-05 (B)35videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[A]23videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
If →a and →b are unit vectors inclined at an angle α, then the value of ∣∣→a−→b∣∣ is
A2sinα2B2cosα2C2sinαD2cosα
For some non zero vector →v, if the sum of →v and the vector obtained from →v by rotating it by an angle 2α equals to the vector obtained from →v by rotating it by α then the value of α, is
View SolutionA particle of mass m is projected with velocity u at an angle α with horizontal. During the period when the particle descends from highest point to the position where
its velocity vector makes an angle α2 with horizontal. Work done by gravity force isView SolutionOne of the surfaces of a biconvex lens of a focal length 10 cm is silvered as shown in figure. Radius of curvature of silvered surface is 10 cm. At a given instant, if speed of object is 1m/s, then the speed of image at that instant is (10+α) m/s. What will be the value of α? (μ=1.5)
View SolutionAn object projected with same speed at two different angles covers the same horizontal range R. If the two times of flight be t1andt2 . The range is 1αgt1t2, the value of α is
View SolutionThe vector cosαcosβˆi+cosαsinβˆj+sinαˆk is a
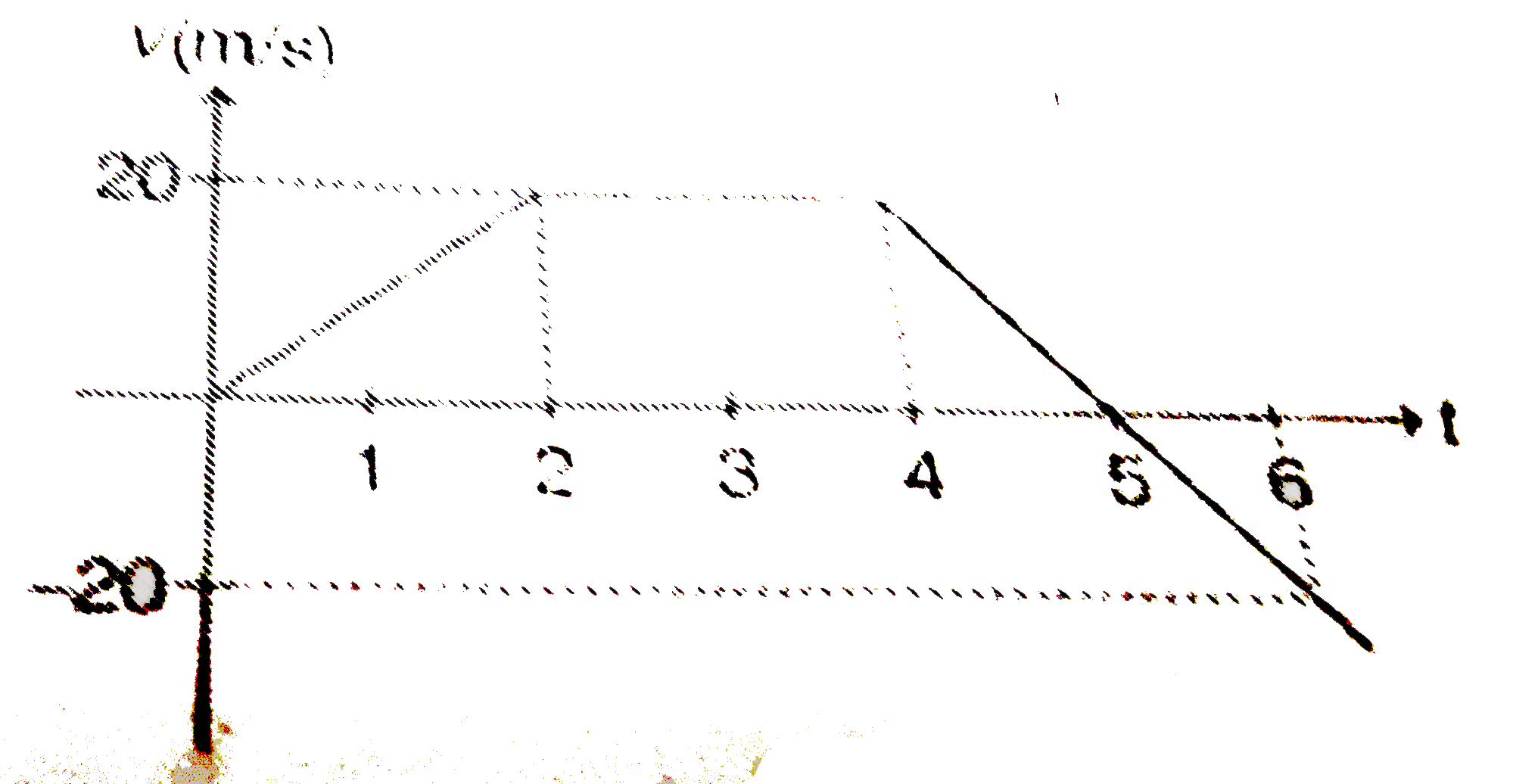
View SolutionFigure shows the velocity time graph for a particle travelling along a straight line. The magnitude of average velocity (in m/s) of particle during the time interval from t=0 to t=6s is 10α. Find the value of α.
View SolutionIf sinα=Asin(α+β),A≠0, then
The value of tanα isView Solution