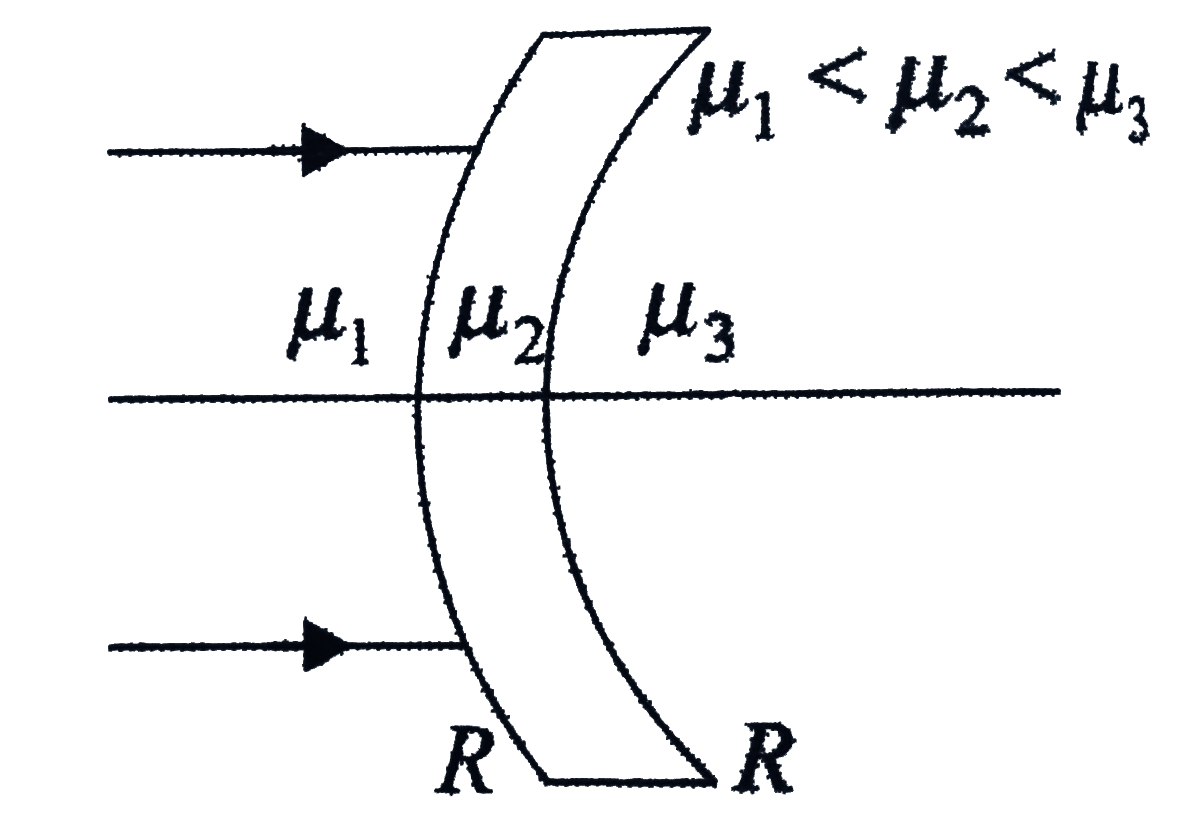
In the figure, light is incident on a thin lens as shown. The radius of curvature for both the surfaces is R. Determine the focal length of this system.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{μ_{3} R}{μ_{3} - μ_{1}}$

For refraction at first surface
$\frac{μ_{2}}{v_{1}} - \frac{μ_{1}}{- \infty} = \frac{μ_{2} - μ_{1}}{+ R} \dots . (i)$
For refraction at second surface ,
$\frac{μ_{3}}{v_{2}} - \frac{μ_{2}}{v_{1}} = \frac{μ_{3} - μ_{2}}{+ R} \dots . . (i i)$
Adding equation (i) and (ii) , we get
$\frac{μ_{3}}{v_{2}} = \frac{μ_{3} - μ_{1}}{R} or v_{2} = \frac{μ_{3} R}{μ_{3} - μ_{1}}$

Therefore , focal lenght of the given lens system is
$\frac{μ_{3} R}{μ_{3} - μ_{1}}$

|

Updated on:21/07/2023

Class 12 PHYSICS RAY OPTICS AND OPTICAL INSTRUMENTS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
What is the refractive index of material of a plano-convex lens , if the radius of curvature of the convex surface is 10 cm and focal length of the lens is 30 cm ?
A $\frac{6}{5}$
B $\frac{7}{4}$
C $\frac{2}{3}$
D $\frac{4}{3}$

ALLEN-GEOMETRICAL OPTICS-subjective

Home
Ask Doubt
Profile