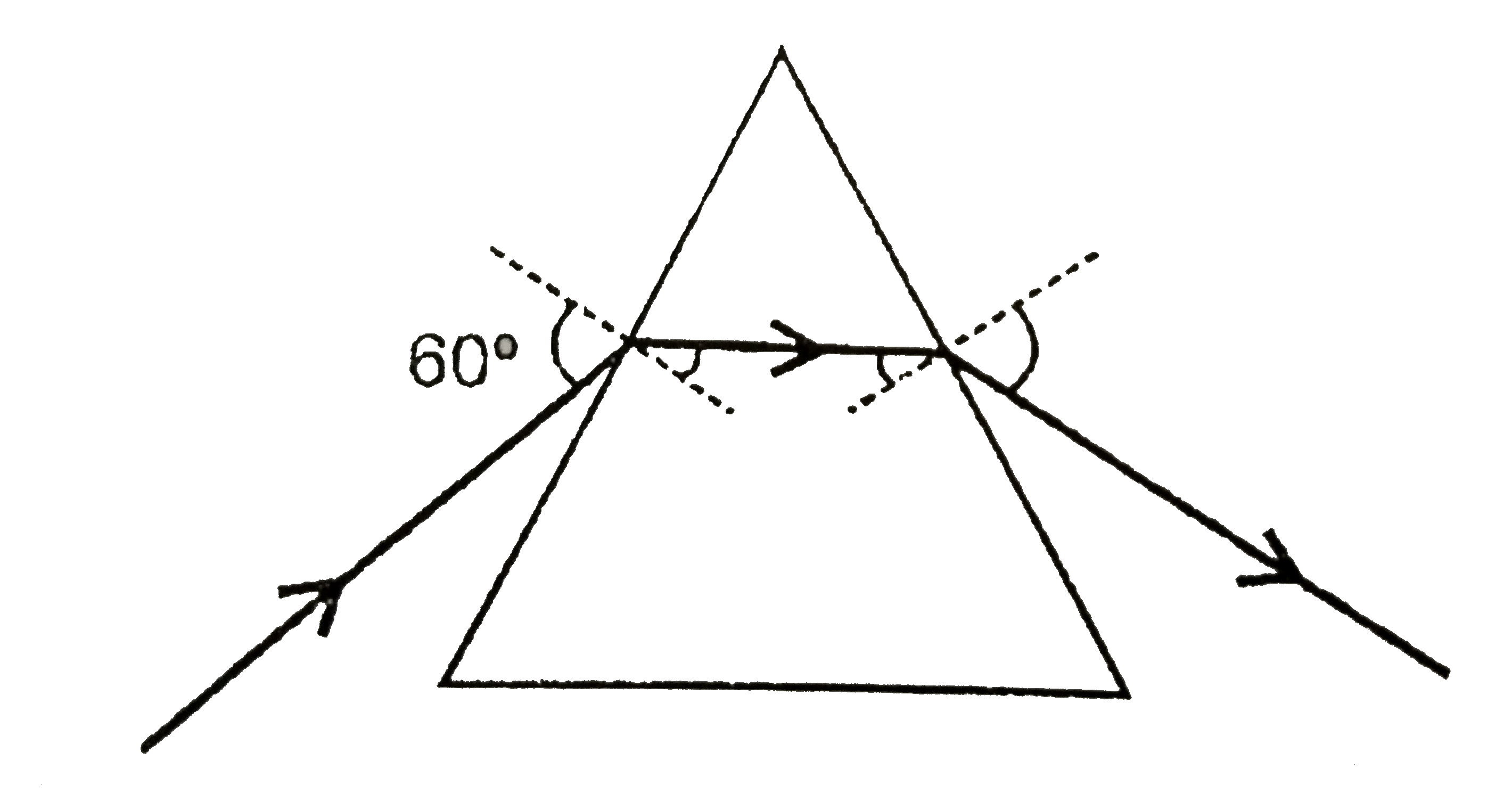
A monochromatic beam of light is incided at $60^{\circ}$ in one face of an equilateral prism of refractive index $n$ and emerges from the opposite face making an angle $θ (n)$ with the normal (see the figure). For $n = \sqrt{3}$ the value of $θ$ is $60^{\circ}$ and $d \frac{θ}{d n} = m$ . The value of $m$ is
$A monochromatic beam of light is incided at 60^(@) in one face of an equilateral prism of refractive index n and emerges from the opposite face making an angle theta(n) with the normal (see the figure). For n=sqrt3 the value of theta is 60^(@) and d(theta)/(dn)=m. The value of m is$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:2

By snell's law
$1 sin 60 = n sin r_{1}$
$\Rightarrow sin r_{1} = \frac{1}{2} r_{1} = 30^{\circ}$ …..(i)
By differentiating 'w.r.t'n
$O = sin r_{1} + n cos r_{1} \frac{d r_{1}}{d n}$
$= \frac{1}{2} + \sqrt{3} (\sqrt{\frac{3}{2}}) \frac{d r_{1}}{d n}$
$\frac{d r_{1}}{d n} = \frac{1}{3}$ .... (ii)
By applying snells's law
$n sin r_{2} = 1 sin θ$
$n sin (60 - r_{1}) = 1 sin θ [∴ A = r_{1} + r_{2}]$
By differentiating 'w.r.t' n
$sin (60 - r_{1}) - n cos (60 - r_{1}) \frac{d r_{1}}{d n} = cos θ \frac{d t h η}{d n}$
By substituting value of $' r_{1}$ ' and $\frac{d r_{1}}{d n}$
from (1) and (2)
$\frac{d θ}{d n} = 2$

|

Updated on:21/07/2023

Class 12 PHYSICS RAY OPTICS AND OPTICAL INSTRUMENTS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A ray of light is incident at $60^{\circ}$ on one face of a prism of angle $30^{\circ}$ and the emergent ray makes $30^{\circ}$ with the incident ray. The refractive index of the prism is
A $1.732$
B $1.414$
C $1.5$
D $1.33$

ALLEN-GEOMETRICAL OPTICS-subjective

Home
Ask Doubt
Profile