The XY plane is the boundary between two tranparednt media. Medium 1 with z≥0 has a refraxtive index of √2 and medium 2 with z≤0 has a refractive index of √3. A ray of light in medium 1 given by the vector 6√3ˆi+8√3ˆj−10ˆk is incident on teh plane of separation. Find the unit vector in the direction of teh refracted ray in medium 2.
The correct Answer is:15√2(3ˆi+4ˆj−5ˆk)
Incident ray
→A=6√3ˆi+8√3ˆj−10ˆk=(6√3ˆi+8√3ˆj)+(−10)ˆk
_E01_245_S01.png)
Q→O+P→Q (As shown in figure )
Note that Q→O is lying on x-y plane .
Note , OQ' and Z-axis are mutually perpendicular .
Hence , we can show them in two- dimensional figure as below .
_E01_245_S02.png)
Vector →A makes an angle i with z-axis , given by
i=cos−1.⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩10√(10)2+(6√3)2+(8√3)2⎫⎪
⎪
⎪
⎪⎬⎪
⎪
⎪
⎪⎭=cos−1{12}
i=60∘
Unit vector in the direction of QOQ' will be
ˆq=6√3ˆi+8√3ˆj√(6√3)2+(8√3)2=15(3ˆi+4ˆj)
Snell's law gives √3√2=sinisinr=sin60∘sinr
∴sinr=√3/2√3/√2=1√2∴r=45∘
Now , we have to find out a unit vector in refracted ray's direction OR . say it is ˆr whose magnitude is 1 .
Thus ˆr=(1sinr)ˆq−(1−cosr)ˆk=1√2(ˆq−ˆk)
=1√2[15(3ˆi+4ˆj)−ˆk]
ˆr=15√2.(3ˆi+4ˆj−5ˆk)
Topper's Solved these Questions
Similar Questions
Let the x-z plane be the boundary between two transparent media. Medium 1 in z≥0 has a refractive index of √2 and medium 2 with z<0 has a refractive index of √3. A ray of light in medium 1 given by the vector →A=6√3ˆi+8√3ˆj−10ˆk is incident on the plane of separation. The angle of refraction in medium 2 is:
View SolutionThe x−y plane is the boundary between two transparent media. Medium-1 with z≤0 has a refractive index √2 and medium -2 with z≤0 has a refractive index √2. A ray of light in medium -1 given by vector A=√3ˆi−ˆk is incident on the plane of separation. The unit vector in the direction of the refracted ray in medium-2 is
View Solution
Knowledge Check
- Question 1 - Select One
A ray of light travelling in the direction 12(ˆi,+√3ˆj) is incident on a plane mirror. After reflection, it travels along the direction 12(ˆi−√3ˆj) . The angle of incidence is
A30∘B45∘C60∘D75∘ - Question 2 - Select One
The refractive index of a medium is √3. What is the angle of refraction, if unpolarizing light is incident on the polarising angle of the medium ?
A60∘B45∘C30∘D0∘
x-y plane separates two media, z≥0 contains a medium of refractive index 1 and z≤0 contains a medium of refractive index 2. A ray of light is incident from first medium along a vectorˆi+ˆj−ˆk. Find the unit vector along the refracted ray.
View SolutionIn the figure shown, the angle made by the light ray with the normal in the medium of refractive index √2 is
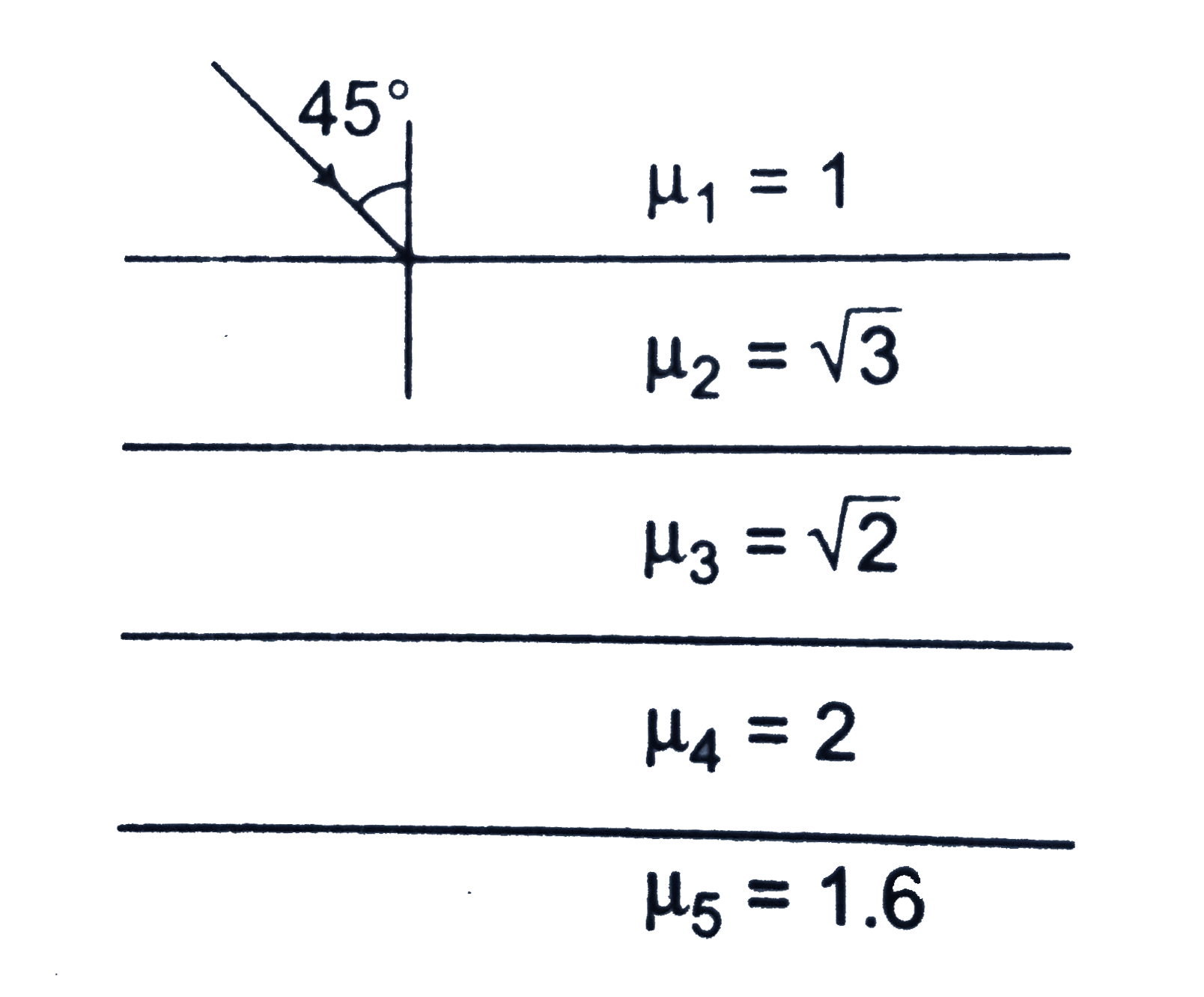 View Solution
View SolutionThe xz plane separates two media A and B with refractive indices μ1 & μ2 respectively. A ray of light travels from A to B. Its directions in the two media are given by the unit vectors, →rA=aˆi+bˆj & →rB=αˆi+βˆj respectively where ˆi & ˆj are unit vectors in the x & y directions. Then :
View SolutionFind a vector in the direction of vector 2ˆi−3ˆj+6ˆk which has magnitude 21 units.
View SolutionThe xz plane separates two media A and B with refractive indices μ1 & μ2 respectively. A ray of light travels from A to B. Its directions in the two media are given by the unut vectors, →rA=aˆi+bˆj & →rBαˆi+βˆj respectively where ˆi & ˆj are unit vectors in the x & y directions. Then :
View SolutionFind a vector in the direction of vector 2ˆi−3ˆj+6ˆk k which has magnitude 21 units.
View Solution

