A ball of mass m kept at the centre of a string of length L is pulled from centre in perpendicular direction and released. Prove that motion of ball is simple harmonic and determine time period of oscillation
To solve the problem of proving that the motion of a ball attached to a string is simple harmonic motion (SHM) and determining the time period of oscillation, we can follow these steps:
Step 1: Understand the Setup
We have a ball of mass m attached to a string of length L. When the ball is pulled perpendicularly from the center and released, it will oscillate about the equilibrium position.
Step 2: Analyze the Forces
When the ball is displaced by a distance x from the equilibrium position, the tension in the string T will create a restoring force. The components of the tension that act to restore the ball to its equilibrium position can be analyzed.
Step 3: Identify the Geometry
Let θ be the angle the string makes with the vertical when the ball is displaced. The vertical component of the tension does not affect the motion, while the horizontal component provides the restoring force.
Step 4: Calculate the Restoring Force
The horizontal component of the tension can be expressed as:
F=−2Tsin(θ)
For small angles, we can use the approximation sin(θ)≈tan(θ)≈xL/2=2xL.
Substituting this into the expression for the restoring force gives:
F=−2T(2xL)=−4TLx
Step 5: Relate Force to Acceleration
According to Newton's second law, the restoring force can also be expressed as:
F=md2xdt2
Setting the two expressions for force equal to each other gives:
md2xdt2=−4TLx
Step 6: Identify the Form of SHM
Rearranging the equation, we have:
d2xdt2=−4TmLx
This is in the form of the standard SHM equation:
d2xdt2=−ω2x
where ω2=4TmL.
Step 7: Determine the Time Period
The angular frequency ω is related to the time period T by the formula:
T=2πω
Substituting for ω:
T=2π√mL4T=2π√mL4T
Final Result
Thus, we have shown that the motion of the ball is simple harmonic and the time period of oscillation is:
T=2π√mL4T
We have a ball of mass m attached to a string of length L. When the ball is pulled perpendicularly from the center and released, it will oscillate about the equilibrium position.
When the ball is displaced by a distance x from the equilibrium position, the tension in the string T will create a restoring force. The components of the tension that act to restore the ball to its equilibrium position can be analyzed.
Let θ be the angle the string makes with the vertical when the ball is displaced. The vertical component of the tension does not affect the motion, while the horizontal component provides the restoring force.
The horizontal component of the tension can be expressed as:
F=−2Tsin(θ)
For small angles, we can use the approximation sin(θ)≈tan(θ)≈xL/2=2xL.
F=−2T(2xL)=−4TLx
According to Newton's second law, the restoring force can also be expressed as:
F=md2xdt2
Setting the two expressions for force equal to each other gives:
md2xdt2=−4TLx
Rearranging the equation, we have:
d2xdt2=−4TmLx
This is in the form of the standard SHM equation:
d2xdt2=−ω2x
where ω2=4TmL.
The angular frequency ω is related to the time period T by the formula:
T=2πω
Substituting for ω:
T=2π√mL4T=2π√mL4T
Thus, we have shown that the motion of the ball is simple harmonic and the time period of oscillation is:
T=2π√mL4T
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES29videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01117videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A mass M is suspended from a spring of negiliglible mass the spring is pulled a little and then released so that the mass executes simple harmonic oscillation with a time period T If the mass is increases by m the time period because (54T),The ratio of mM is
View SolutionConsider the situation shown in figure. Show that if the blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.
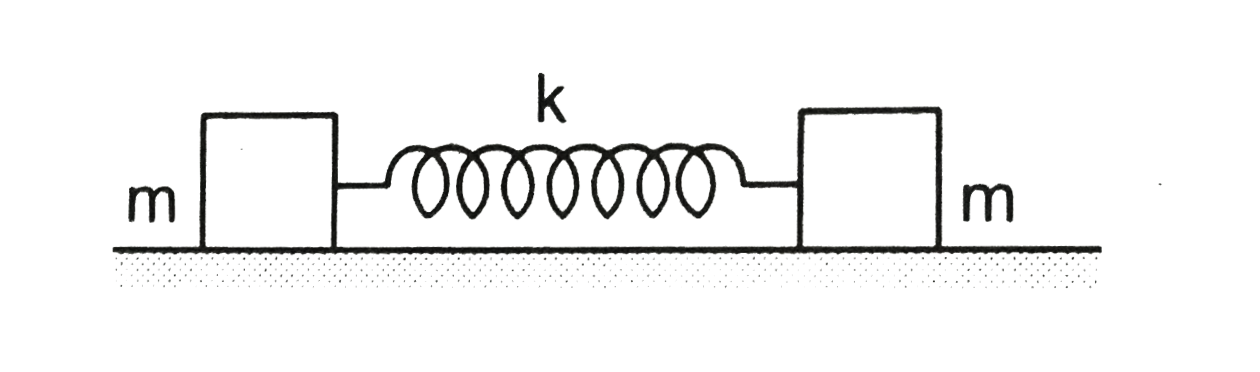 View Solution
View Solution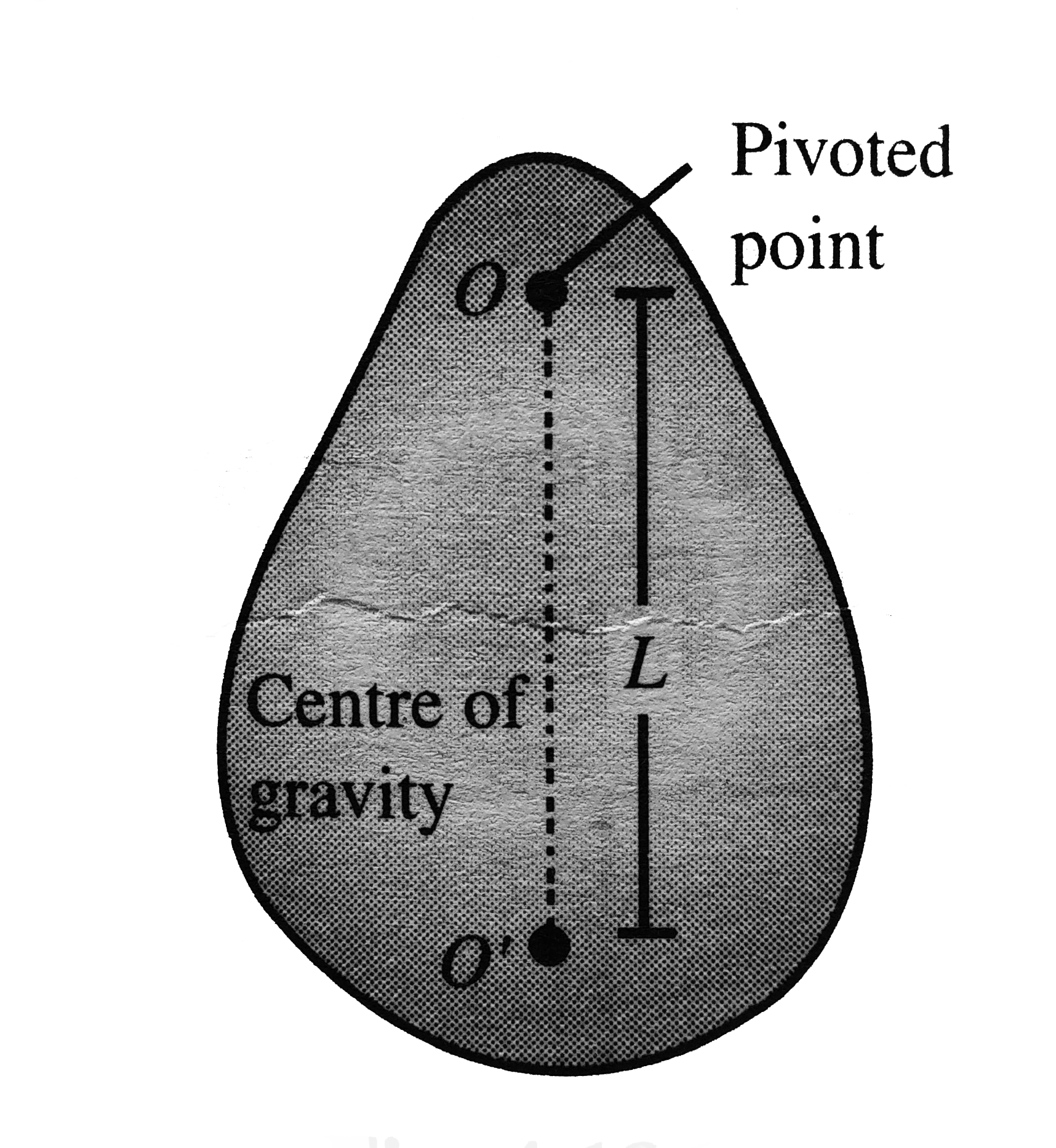
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.View SolutionConsider the situastion shown in figure. Show that if that blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.
 View Solution
View SolutionA cubical wood piece of mass 13.5 gm and volume 0.0027m3 float in water. It is depressed and released, then it executes simple harmonic motion. Calculate the period of oscillation ?
View SolutionIs oscillation of a mass suspended by a spring simple harmonic ? give expression for its time period also.
View SolutionA ball of mass, m is attractive to two springwhich are already stretched so that each pulls on to ball with a force F. length of each spring . In this Determine the period of small oscillations of the ball in a difference perpendicular of length of psirng. Difference of the mass of spring and gravity .
 View Solution
View SolutionA mass M is suspended from a spring of negligible mass. The spring is pulled a little then released, so that the mass executes simple harmonic motion of time period T. If the mass is increased by m, the time period becomes 5T3. Find the ratio of m/M.
View SolutionA plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
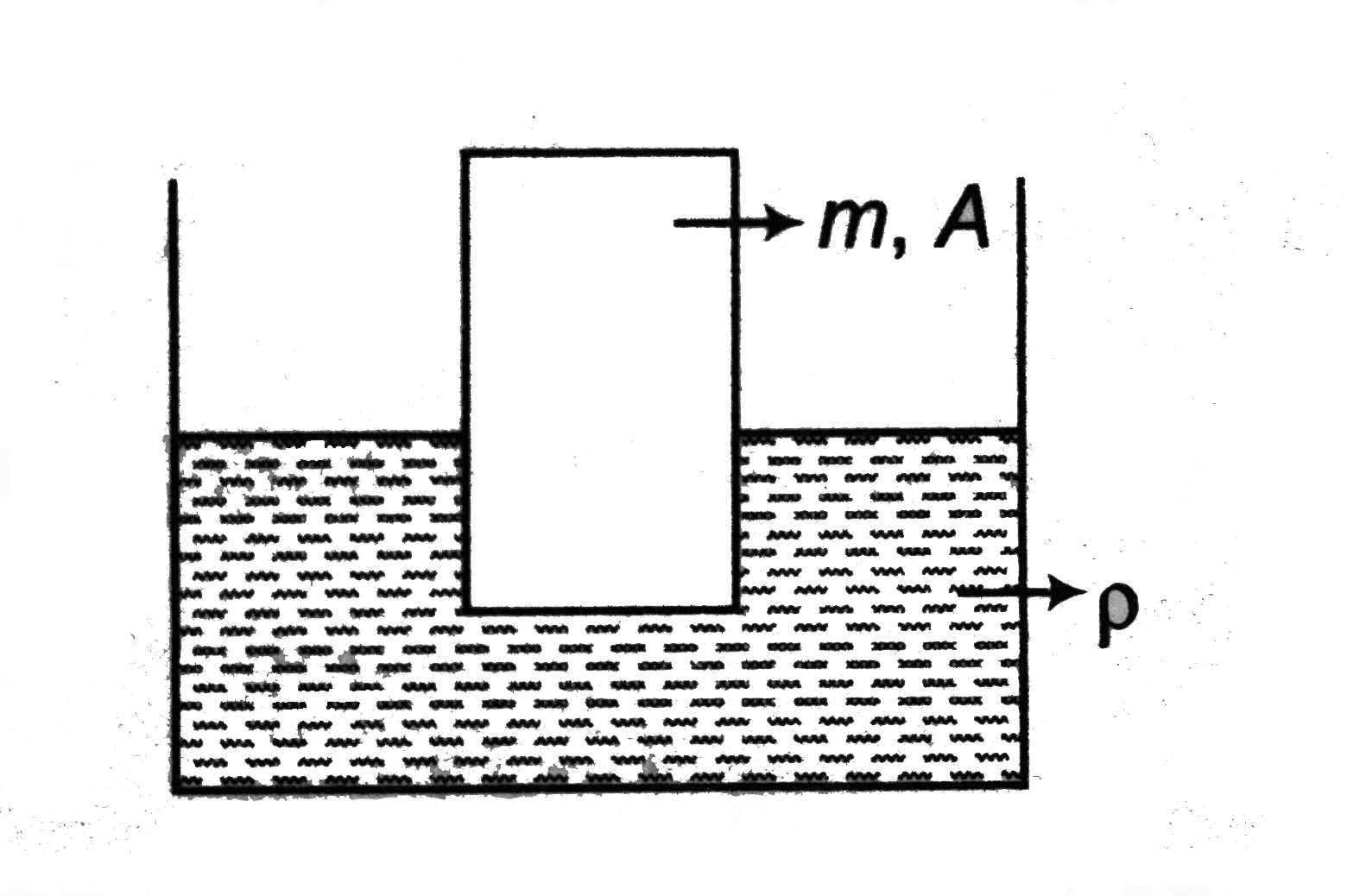 View Solution
View SolutionThe maximum velocity of a particle, excuting simple harmonic motion with an amplitude 7mm, is 4.4m/s The period of oscillation is.
View Solution

