Two particles A to B perform SHM along the same stright line with the same amplitude 'a' same frequency 'f' and same equilbrium position 'O'. The greatest distance between them is found to be 3a/2. At some instant of time they have the same displacement from mean position. what is the displacement?
a/2
a√7/4
√3/a2
3a/4
The correct Answer is:B
To solve the problem step by step, we will analyze the motion of the two particles A and B performing Simple Harmonic Motion (SHM) and find the required displacement.
Step 1: Understanding the Setup
Both particles A and B perform SHM along the same straight line with:
- Amplitude = a
- Frequency = f
- Equilibrium position = O
The greatest distance between them is given as 3a2.
Step 2: Maximum Displacement Analysis
Since the maximum distance between the two particles is 3a2, we can express this in terms of their displacements from the equilibrium position. Let the displacements of A and B from the mean position O be xA and xB respectively.
The maximum distance can be expressed as:
|xA−xB|=3a2
Step 3: Equal Frequency and Amplitude
Since both particles have the same amplitude and frequency, we can assume that at the point of maximum separation, they are at the following positions:
- Particle A is at xA=3a4
- Particle B is at xB=−3a4
This gives:
|3a4−(−3a4)|=3a2
Step 4: Finding the Condition for Same Displacement
At some instant, both particles have the same displacement from the mean position. This means:
xA=xB
Let’s denote this common displacement as x.
Step 5: Using Trigonometric Relationships
From the triangle formed by the displacements, we can use trigonometric identities. We know:
sinθ=34
From this, we can find cosθ:
cos2θ+sin2θ=1
cos2θ=1−sin2θ=1−(34)2=1−916=716
Thus,
cosθ=√74
Step 6: Finding the Displacement
The displacement x can be expressed in terms of the amplitude a and cosθ:
x=acosθ=a⋅√74
Final Answer
Thus, the displacement from the mean position is:
x=√7a4
Both particles A and B perform SHM along the same straight line with:
- Amplitude = a
- Frequency = f
- Equilibrium position = O
Since the maximum distance between the two particles is 3a2, we can express this in terms of their displacements from the equilibrium position. Let the displacements of A and B from the mean position O be xA and xB respectively.
|xA−xB|=3a2
Since both particles have the same amplitude and frequency, we can assume that at the point of maximum separation, they are at the following positions:
- Particle A is at xA=3a4
- Particle B is at xB=−3a4
|3a4−(−3a4)|=3a2
At some instant, both particles have the same displacement from the mean position. This means:
xA=xB
Let’s denote this common displacement as x.
From the triangle formed by the displacements, we can use trigonometric identities. We know:
sinθ=34
From this, we can find cosθ:
cos2θ+sin2θ=1
cos2θ=1−sin2θ=1−(34)2=1−916=716
Thus,
cosθ=√74
The displacement x can be expressed in terms of the amplitude a and cosθ:
x=acosθ=a⋅√74
Thus, the displacement from the mean position is:
x=√7a4
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-0219videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column1videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES29videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
Two particle A and B execute SHM along the same line with the same amplitude a, same frequency and same equlibrium position O. If the phase difference between them is ϕ=2sin−1(0.9) then find maxium distance between two.
View SolutionTwo particles are performing SHM in same phase. It means that
View SolutionTwo particle execute SHM of same amplitude of 20cm with same period along the same line about the same equilibrium position. The maximum distance between the two is 20cm. Their phase difference in radians is
View SolutionTwo particle P and Q describe S.H.M. of same amplitude a same frequency f along the same straight line .The maximum distance between the two particles is a√2 The phase difference between the two particle is
View SolutionTwo particle P and Q describe S.H.M. of same amplitude a same frequency f along the same straight line .The maximum distance between the two particles is a√2 The phase difference between the two particle is
View SolutionThe figure shows a graph between velocity and displacement (from mean position) of a particle performing SHM:
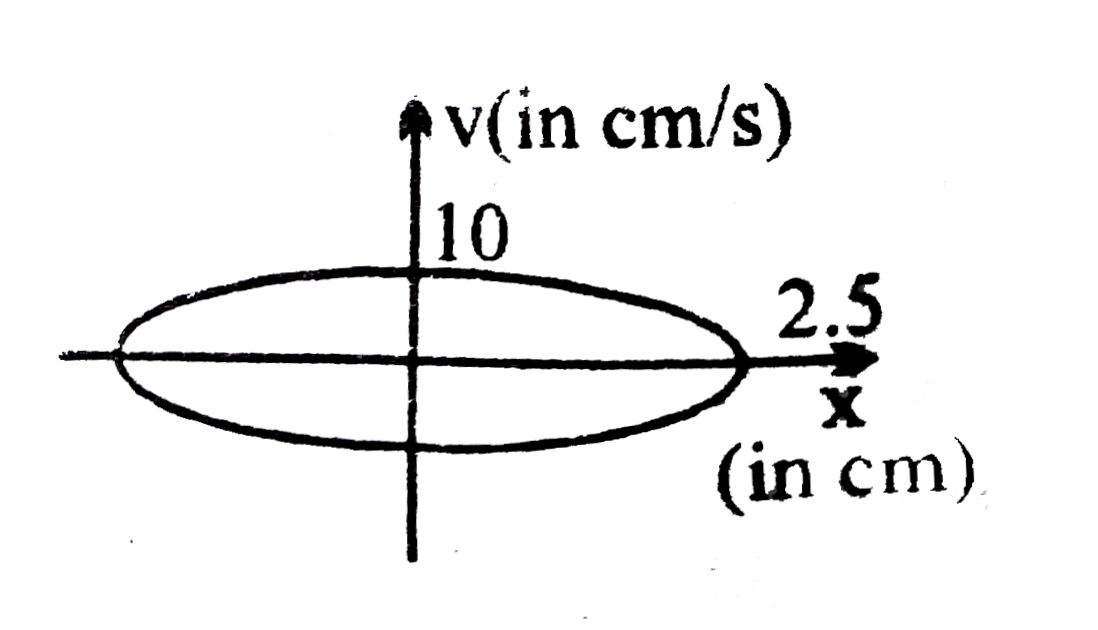 View Solution
View SolutionTwo particles of equal mass are moving along the same straight line with the same speed in opposite direction. What is the speed of the centre of mass of the system ?
View SolutionTwo particles of equal mass are moving along the same straight line with the same speed in opposite direction. What is the speed of the centre of mass of the system ?
View SolutionA partical excutes SHM with same frequency and amplitude along the same straight line. They cross each other , at a point midway between the mean and the exterme position. Find the Phase difference between them.
View SolutionTwo particles move parallel to x - axis about the origin with the same amplitude and frequency. At a certain instant they are found at distance A3 from the origin on opposite sides but their velocities are found to be in the same direction. What is the phase difference between the two ?
View Solution

