Two identical springs are fixed at one end and masses 1kg and 4kg are suspended at their other ends. They are both strethced down form their mean position and let go simultaneously. If they are in the same phase after every 4 seconds then the springs constant k is
πNm
π2Nm
2πNm
given data is insufficient
The correct Answer is:B
To solve the problem, we need to find the spring constant k given that two masses (1 kg and 4 kg) suspended from identical springs are in the same phase after every 4 seconds.
1. Identify the Masses and Their Corresponding Angular Frequencies:
- Let m1=1kg and m2=4kg.
- The angular frequency ω for a mass-spring system is given by:
ω=√km
- Therefore, for mass m1:
ω1=√k1=√k
- For mass m2:
ω2=√k4=12√k
2. Determine the Condition for Same Phase:
- The two systems will be in the same phase when the difference in their angular frequencies multiplied by time is an integer multiple of 2π:
ω1t−ω2t=2nπ
- Substituting the expressions for ω1 and ω2:
√kt−12√kt=2nπ
- Simplifying this gives:
(√k−12√k)t=2nπ
12√kt=2nπ
3. Using Given Time Interval:
- We know that they are in the same phase every 4 seconds, so let t=4 seconds:
12√k⋅4=2nπ
- This simplifies to:
2√k=2nπ
- Dividing both sides by 2:
√k=nπ
4. Finding the Spring Constant k:
- For n=1 (the first occurrence of being in phase):
√k=π
- Squaring both sides gives:
k=π2
Final Answer:
The spring constant k is:
π2N/m
- Let m1=1kg and m2=4kg.
- The angular frequency ω for a mass-spring system is given by:
ω=√km
- Therefore, for mass m1:
ω1=√k1=√k
- For mass m2:
ω2=√k4=12√k
- The two systems will be in the same phase when the difference in their angular frequencies multiplied by time is an integer multiple of 2π:
ω1t−ω2t=2nπ
- Substituting the expressions for ω1 and ω2:
√kt−12√kt=2nπ
- Simplifying this gives:
(√k−12√k)t=2nπ
12√kt=2nπ
- We know that they are in the same phase every 4 seconds, so let t=4 seconds:
12√k⋅4=2nπ
- This simplifies to:
2√k=2nπ
- Dividing both sides by 2:
√k=nπ
- For n=1 (the first occurrence of being in phase):
√k=π
- Squaring both sides gives:
k=π2
The spring constant k is:
π2N/m
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column1videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Match The Column9videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01117videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
From the fixed pulley, masses 2kg, 1kg and 3kg are suspended as shown in the figure. Find the extension in the spring if k=100N/m. (Neglect oscillations due to spring)
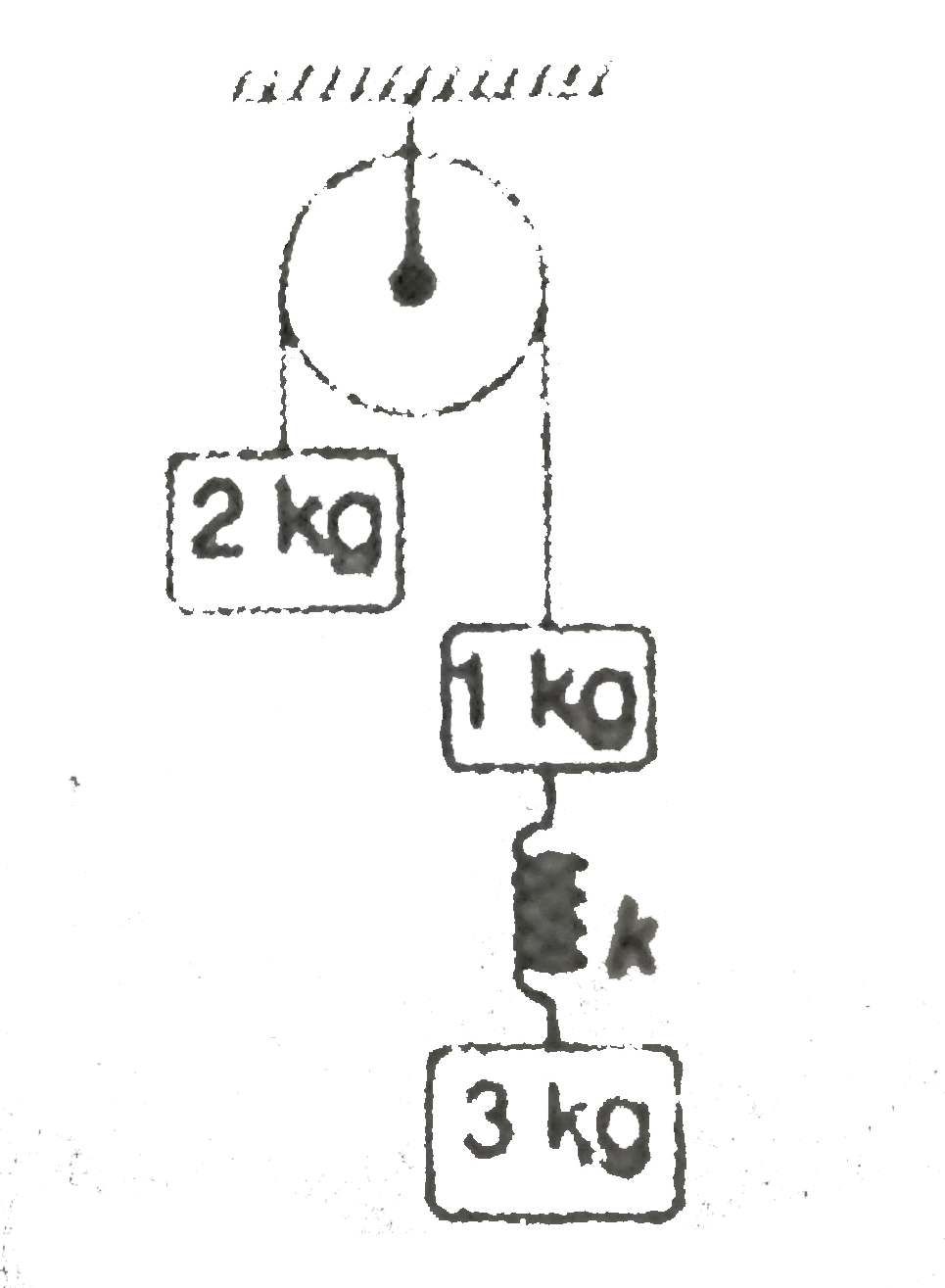 View Solution
View SolutionFigure a) shows a spring of force constant k clamped rigidly at once end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?
 View Solution
View SolutionFigure a) shows a spring of force constant k clamped rigidly at once end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?
 View Solution
View SolutionA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
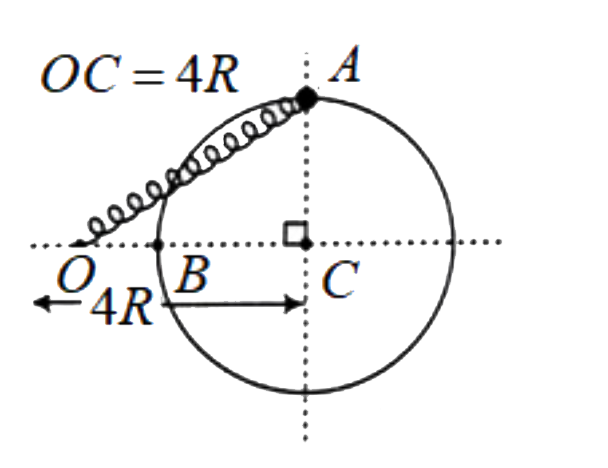 View Solution
View SolutionA body of mass m is suspended from vertical spring and is set into simple harmonic oscillations of time period T. Next the spring is fixed at one end on a smooth horizontal table and same body is attached at the other end. The body is pulled slightly and then released to produce horizontal oscillations of the spring. The time period of horizontal oscillations is
View SolutionA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is
 View Solution
View SolutionA light pulley is suspended at the lower end of a spring of constant k1, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k2. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.
 View Solution
View Solution
Figure. (a) shows a spring of force constant k fixed at one end and carrying a mass m at the other end placed on a horizontal frictionless surface. The spring is stretched by a force F. Figure. (b) shows the same spring with both endsf free and a mass m fixed at each free end Each of the spring is streched by the same force F. The mass in case (a) and the masses in case (b) are then released. Which of the following statements are true?View SolutionForce constant of a weightless spring is 16Nm−1. A body if mass 1 kg suspended from it is pulled down through 5 cm from its mean position and then released. The maximum kinetic energy of the body will be
View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View Solution

