A horizontal plank has a rectangular block placed on it. The plank starts oscillating vertically and simple harmonically with an amplitude of 40 cm. The block just loses contact with the plank when the latter is at momentary rest Then.
the period of oscillation is (2π5)
the block weight double of its weight, when the plank is at opne of the positions of momentary rest
the block weight 0.5 times its weight on the plank halfway up
the block weighs 1.5 times its weight on the plank halfway down
The correct Answer is:A, B, C, D
To solve the problem step by step, we will analyze the situation where a rectangular block placed on a plank loses contact with the plank when the plank is at its momentary rest during vertical oscillation.
Step 1: Understand the Problem
We have a plank that oscillates vertically with a certain amplitude, and we need to find the time period of this oscillation when the block just loses contact with the plank.
Step 2: Identify Given Data
- Amplitude of oscillation (A) = 40 cm = 0.4 m (converted to meters for standard SI units)
- The block loses contact with the plank when the plank is at its momentary rest.
Step 3: Analyze Forces at the Point of Losing Contact
When the block loses contact with the plank, the normal force (N) acting on the block becomes zero. At this point, the only forces acting on the block are its weight (mg) and the pseudo force due to the acceleration of the plank.
Step 4: Write Down the Equation for Maximum Acceleration
The maximum acceleration (a_max) of the plank during simple harmonic motion is given by:
amax=A⋅ω2
where:
- A is the amplitude,
- ω is the angular frequency.
At the point of losing contact, this maximum acceleration must equal the acceleration due to gravity (g):
A⋅ω2=g
Step 5: Substitute Known Values
We know:
- A = 0.4 m,
- g = 10 m/s² (approximately).
Substituting these values into the equation:
0.4⋅ω2=10
Step 6: Solve for Angular Frequency (ω)
Rearranging the equation gives:
ω2=100.4=25
Taking the square root:
ω=√25=5 rad/s
Step 7: Calculate the Time Period (T)
The time period (T) of oscillation is given by:
T=2πω
Substituting the value of ω:
T=2π5 seconds
Final Answer
The time period of oscillation is:
T=2π5 seconds
---
We have a plank that oscillates vertically with a certain amplitude, and we need to find the time period of this oscillation when the block just loses contact with the plank.
- Amplitude of oscillation (A) = 40 cm = 0.4 m (converted to meters for standard SI units)
- The block loses contact with the plank when the plank is at its momentary rest.
When the block loses contact with the plank, the normal force (N) acting on the block becomes zero. At this point, the only forces acting on the block are its weight (mg) and the pseudo force due to the acceleration of the plank.
The maximum acceleration (a_max) of the plank during simple harmonic motion is given by:
amax=A⋅ω2
where:
- A is the amplitude,
- ω is the angular frequency.
A⋅ω2=g
We know:
- A = 0.4 m,
- g = 10 m/s² (approximately).
0.4⋅ω2=10
Rearranging the equation gives:
ω2=100.4=25
Taking the square root:
ω=√25=5 rad/s
The time period (T) of oscillation is given by:
T=2πω
Substituting the value of ω:
T=2π5 seconds
The time period of oscillation is:
T=2π5 seconds
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column1videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Match The Column9videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01117videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A horizontal platform with a small block of mass 1 kg kept on it performs vertical SHM of amplitude 1 cm. The block does not lose contact with the platform anywhere. The minimum possible time period of the platform
View SolutionPassage III A block of mass m =1/2 kg is attached with two springs each of force contant k=10N/m as shown. The block is oscillating vertically up and down with amplitude A=25cm. When the block is at its mean position one of the spring breaks without changing momentum of block.
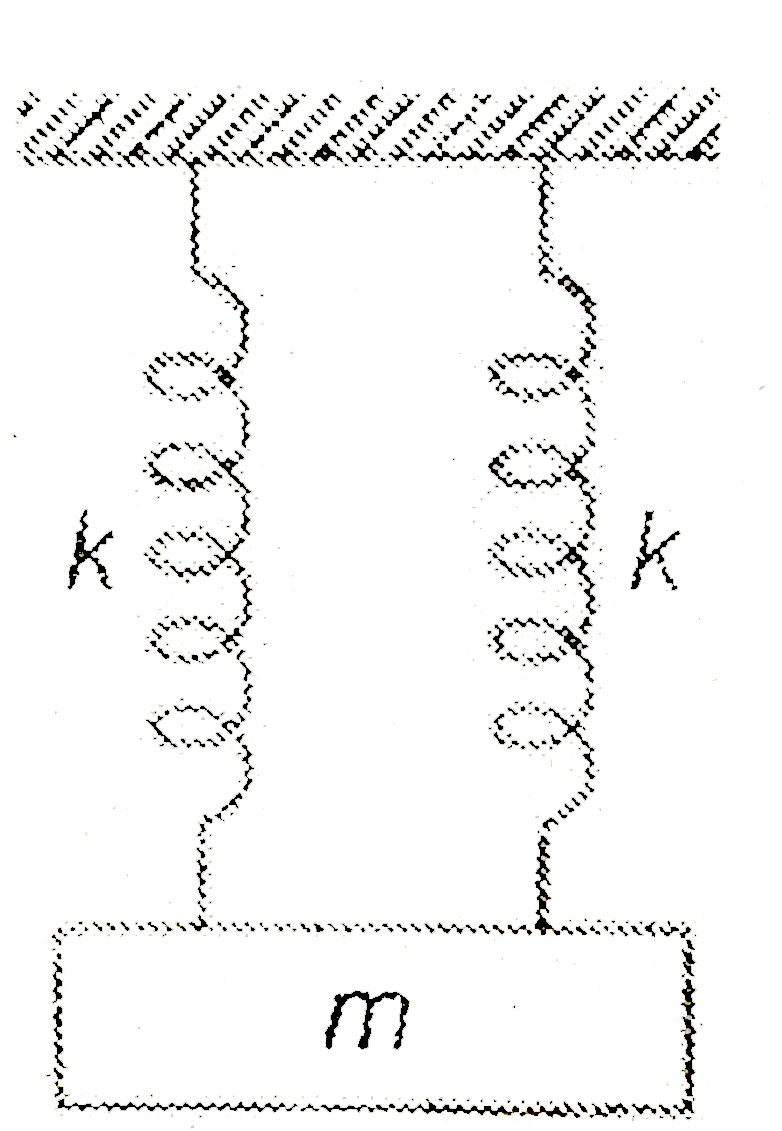
What is the new amplitude of osciallation of the block.View SolutionPassage III A block of mass m =1/2 kg is attached with two springs each of force contant k=10N/m as shown. The block is oscillating vertically up and down with amplitude A=25cm. When the block is at its mean position one of the spring breaks without changing momentum of block.
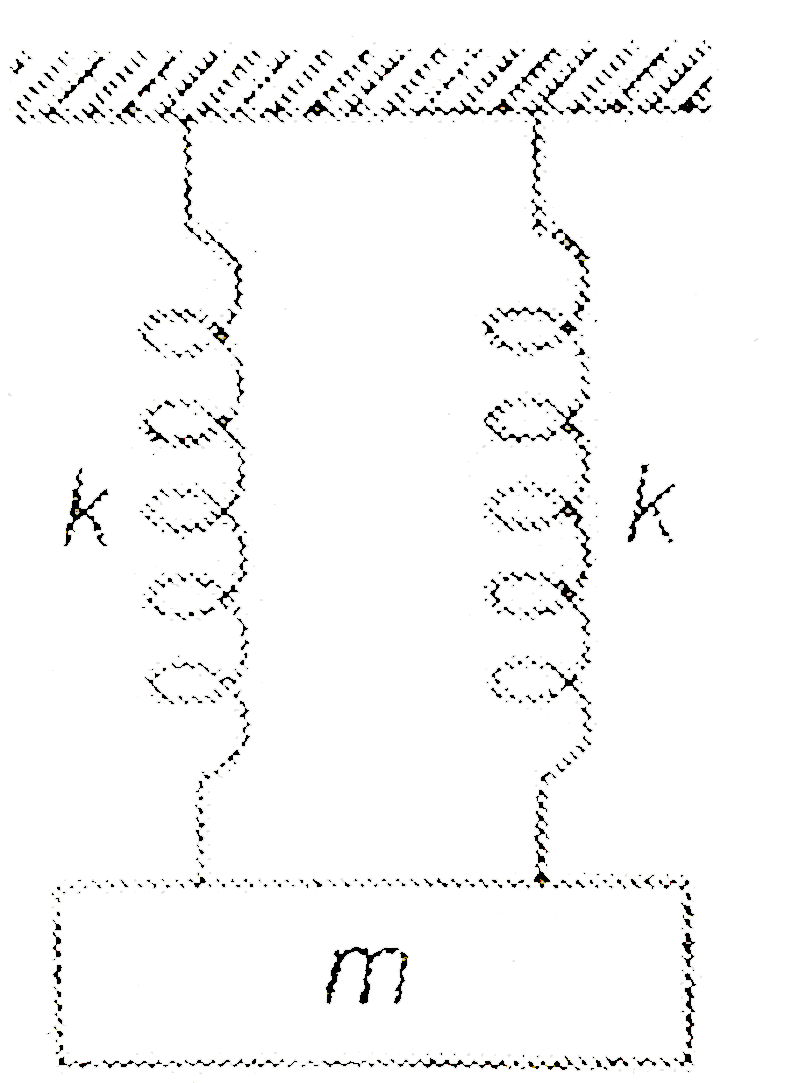
If instead of breaking one spring m/2 mass would have fallen from the block, then what will be the new amplitude?View SolutionA plank with a small block on top of it is under going vertical SHM. Its period is 2sec. The minium amplitude at which the block will separate from plank is :
View Solution
A plank of mass 12 kg is supported by two identical springs as shown is Fig. The plank always remains horizontal. When the plank is pressed down and released it performs simple harmonic motion with time period 3 s. When a block of m is attached to the plank the time priod changes to 6 s. The mass of the block isView SolutionA block is kept is kept over a horizontal platform, executing vertical SHM of angular frequency ω. Find maximum amplitude of oscillations, so that the block does not leave contact with the platform.
 View Solution
View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View SolutionA block of mass m is kept on a plank . The coefficient of friction between the plank and block is 1. The plank is slowly raised from one end so that it makes angle θ with horizontal . The forces of friction acting on the plank , when θ=30∘andθ60∘ are respectively,
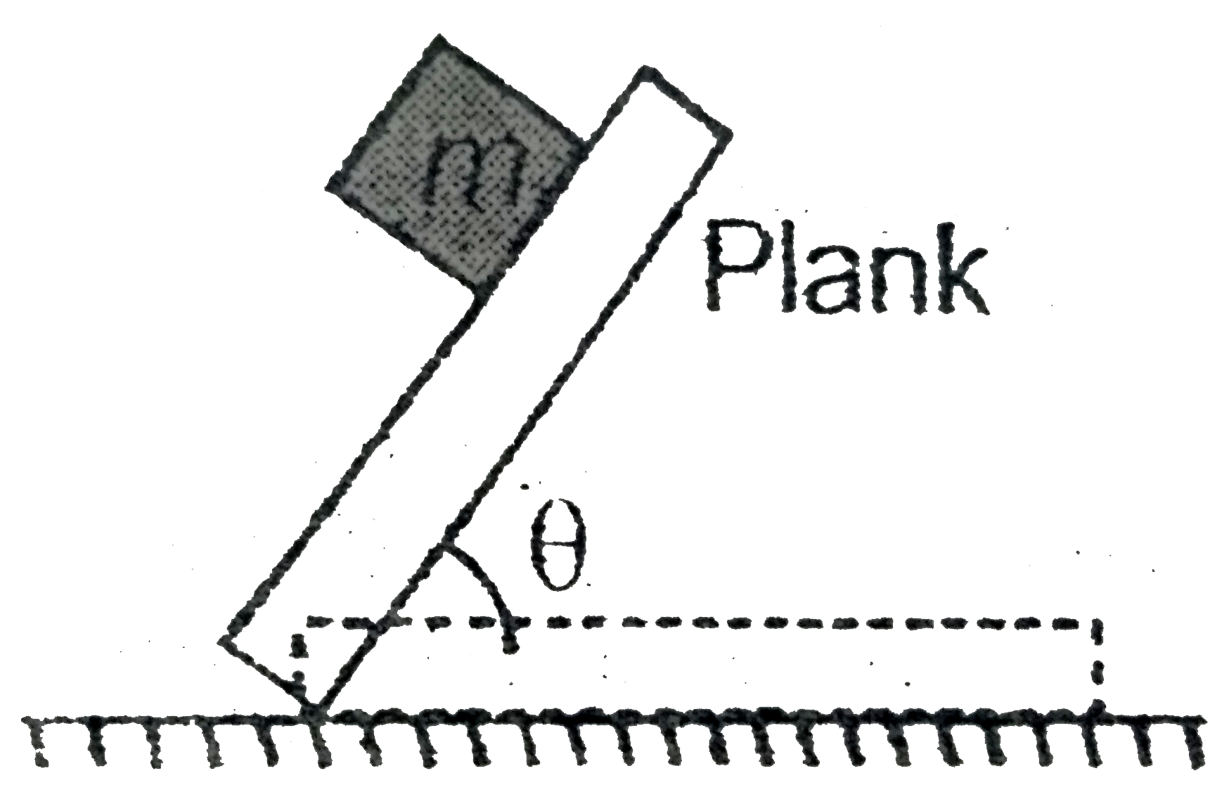 View Solution
View SolutionA horizontal plane supports a plank with a block placed on it. A light elastic string is attached to the block, which is attached to a fixed point O. Initially, the cord is unstretched and vertical. The plank is slowly shifted to right until the block starts sliding over it. It occurs at the moment when the cord deviates from vertical by an angle θ=0∘. Work done by the force F equals
 View Solution
View SolutionA horizontal plane supports a plank with a bar of mass m placed on it and attached by a light elastic non-deformed cord of length l0, to a point O. The coefficient of friciton between the bar and the plank is equal to m. The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord derivates from the vertical by an angle θ.
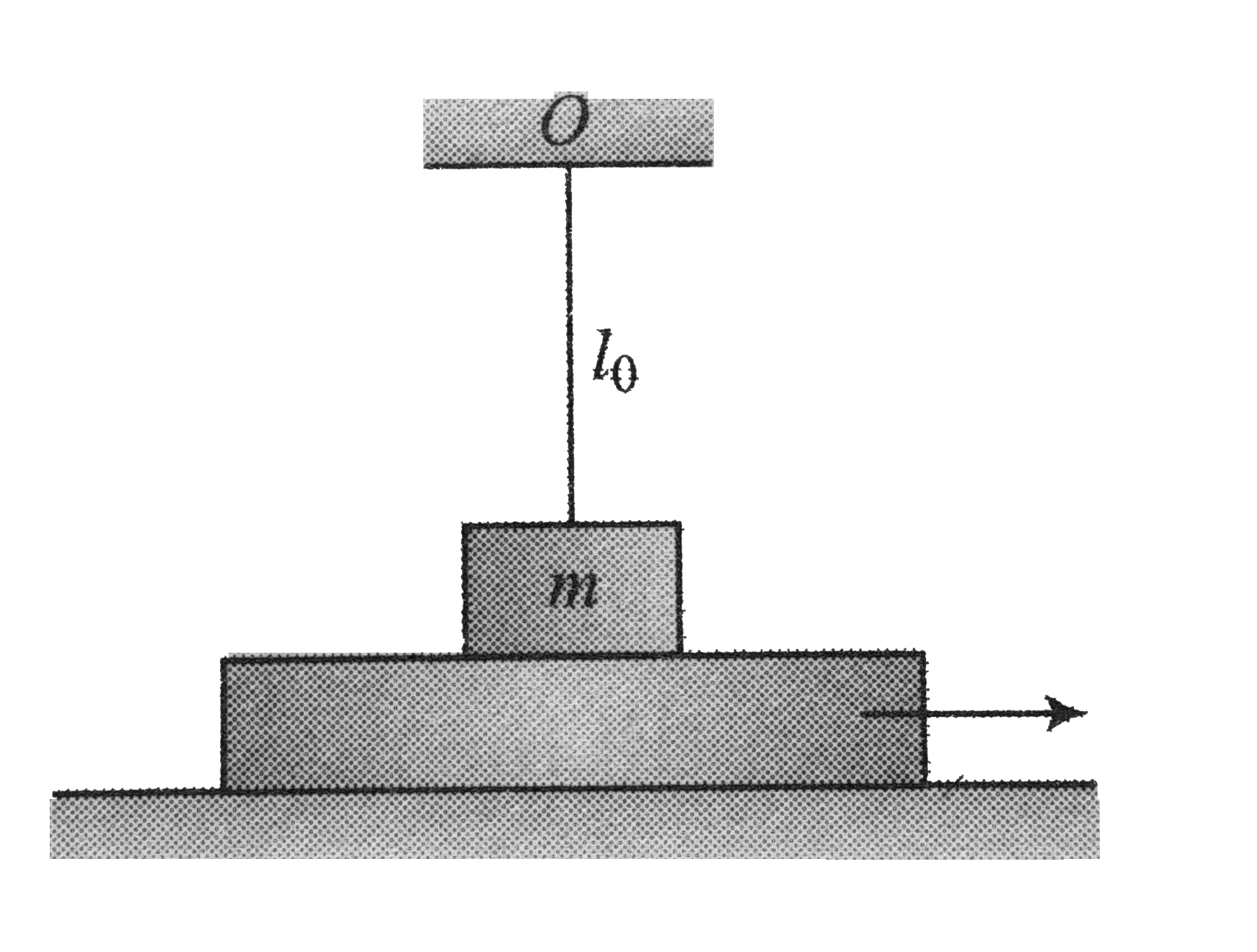
Find the work that has been performed by the moment by the frictional force acting on the bar in the reference frame fixed to the plane.View Solution

