Question

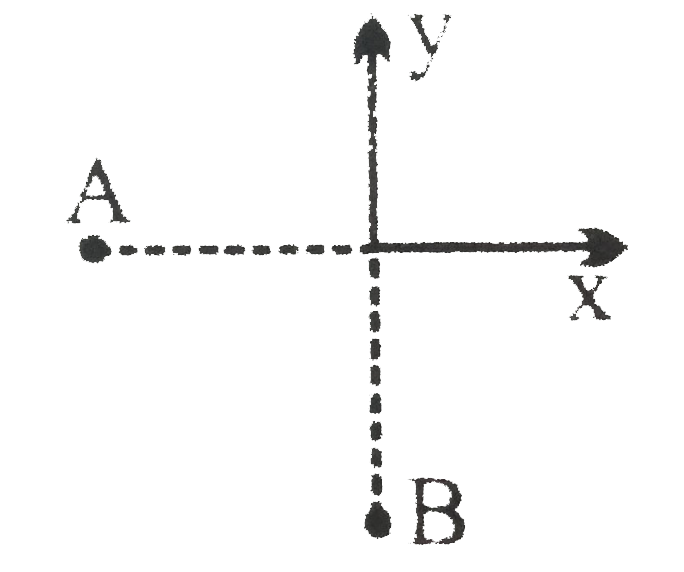
Two particles ${\displaystyle A}$ and ${\displaystyle B}$ performing ${\displaystyle SHM}$ along ${\displaystyle x}$ and ${\displaystyle y-}$axis respectively with equal amplitude and frequency of ${\displaystyle 2cm}$ and ${\displaystyle 1Hz}$ respectively. Equilibrium positions of the particles ${\displaystyle A}$ and ${\displaystyle B}$ are at the co-ordinates ${\displaystyle (3,0)}$ and ${\displaystyle (0,4)}$ respectively. At ${\displaystyle t=0,B}$ is at its equilibrium positions and moving towards the origin, while ${\displaystyle A}$ is nearest to the origin and moving away from the origin. If the maximum and minimum distances between ${\displaystyle A}$ and ${\displaystyle B}$ is ${\displaystyle s_1}$ and ${\displaystyle s_2}$ then find ${\displaystyle s_1+s_2}$ (in ${\displaystyle cm}$).

Options

A. `x = (2 cm) cos 2pit`
B. `x = (3 cm) - (2 cm) cos 2 pit`
C. `x = (2 cm) sin 2 pit`
D. `x = (3 cm) - (2 cm) sin 2pit`

Answer

B

Explanation

As A is at its negative extreme at `t = 0`
so `x - 3 = 2 sin (2pit + 3pi//2) rArr x = 3-2 cos (2pit)`