An object of mass m is moving in unifrom circular motion in xy-plane. The circle has radius R and object is moving clockwise around the circle with speed v. The motion is projected onto the x-axis where it appears as simple harmonic motion accoding to x(t)=Rcos(ωt+ϕ). The motion starts from pointof coordinates
(0,R)
In this projection ω is -
v/R
m2/R
R/v
None of these
The correct Answer is:A
To solve the problem, we need to determine the angular frequency ω of the object moving in uniform circular motion, which is projected onto the x-axis as simple harmonic motion (SHM).
1. Understanding Circular Motion:
- The object of mass m is moving in a circle of radius R with a constant speed v.
- The coordinates of the object at any time t can be represented in terms of the angle θ(t) it makes with the x-axis.
2. Angular Frequency Definition:
- The angular frequency ω is defined as the rate of change of the angle with respect to time. It is given by the formula:
ω=2πT
where T is the time period of one complete revolution.
3. Finding the Time Period:
- The time period T can be calculated using the circumference of the circle and the speed:
T=CircumferenceSpeed=2πRv
4. Substituting Time Period into Angular Frequency:
- Now substituting T into the formula for ω:
ω=2πT=2π2πRv=vR
5. Conclusion:
- Therefore, the angular frequency ω of the motion projected onto the x-axis is:
ω=vR
Final Answer:
The angular frequency ω is vR.
- The object of mass m is moving in a circle of radius R with a constant speed v.
- The coordinates of the object at any time t can be represented in terms of the angle θ(t) it makes with the x-axis.
- The angular frequency ω is defined as the rate of change of the angle with respect to time. It is given by the formula:
ω=2πT
where T is the time period of one complete revolution.
- The time period T can be calculated using the circumference of the circle and the speed:
T=CircumferenceSpeed=2πRv
- Now substituting T into the formula for ω:
ω=2πT=2π2πRv=vR
- Therefore, the angular frequency ω of the motion projected onto the x-axis is:
ω=vR
The angular frequency ω is vR.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (5)
3 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [A]
20 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (3)
2 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A particle moves on the X-axis according to the equation x=x0sin2ωt. The motion simple harmonic
View SolutionFor a particle in uniform circular motion , the acceleration →a at a point p(R,θ) on the circle of radiu R is ( Here θ is measured from the x−aξs )
View SolutionFor a particle in uniform circular motion the acceleration a at a point P(R,θ) on the circle of radius R is (here 'v' is the speed of the particle and θ is measured from the x-axis)
View SolutionFor a particle in uniform circular motion the acceleration →a at a point P(R,θ) on the circle of radius R is : ( here θ is measured from the x- axis )
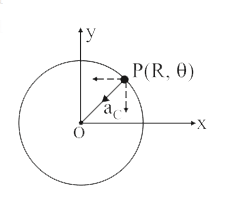
View SolutionIf an object of mass m moves in uniform circular motion, a formce F acts on it, whose direction is always towards the centre of the circular path. If F depends on m, speed v of the object and radius r of the circular path, find an expression for F.
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
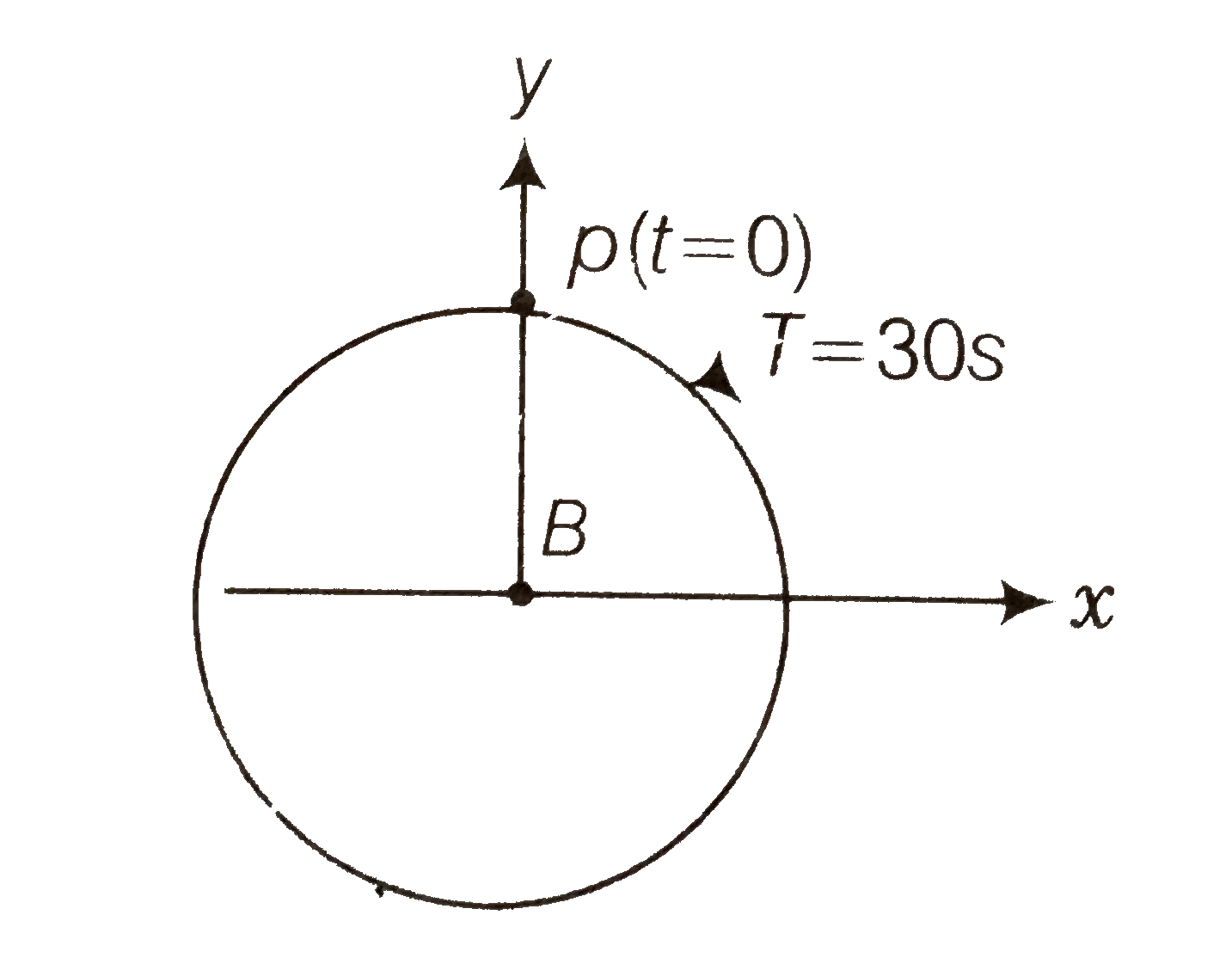
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
View SolutionA particle moves in the x−y plane , accoding to the equation, r=(ˆi+2ˆj)Acosωt. The motion of the particle is
View Solution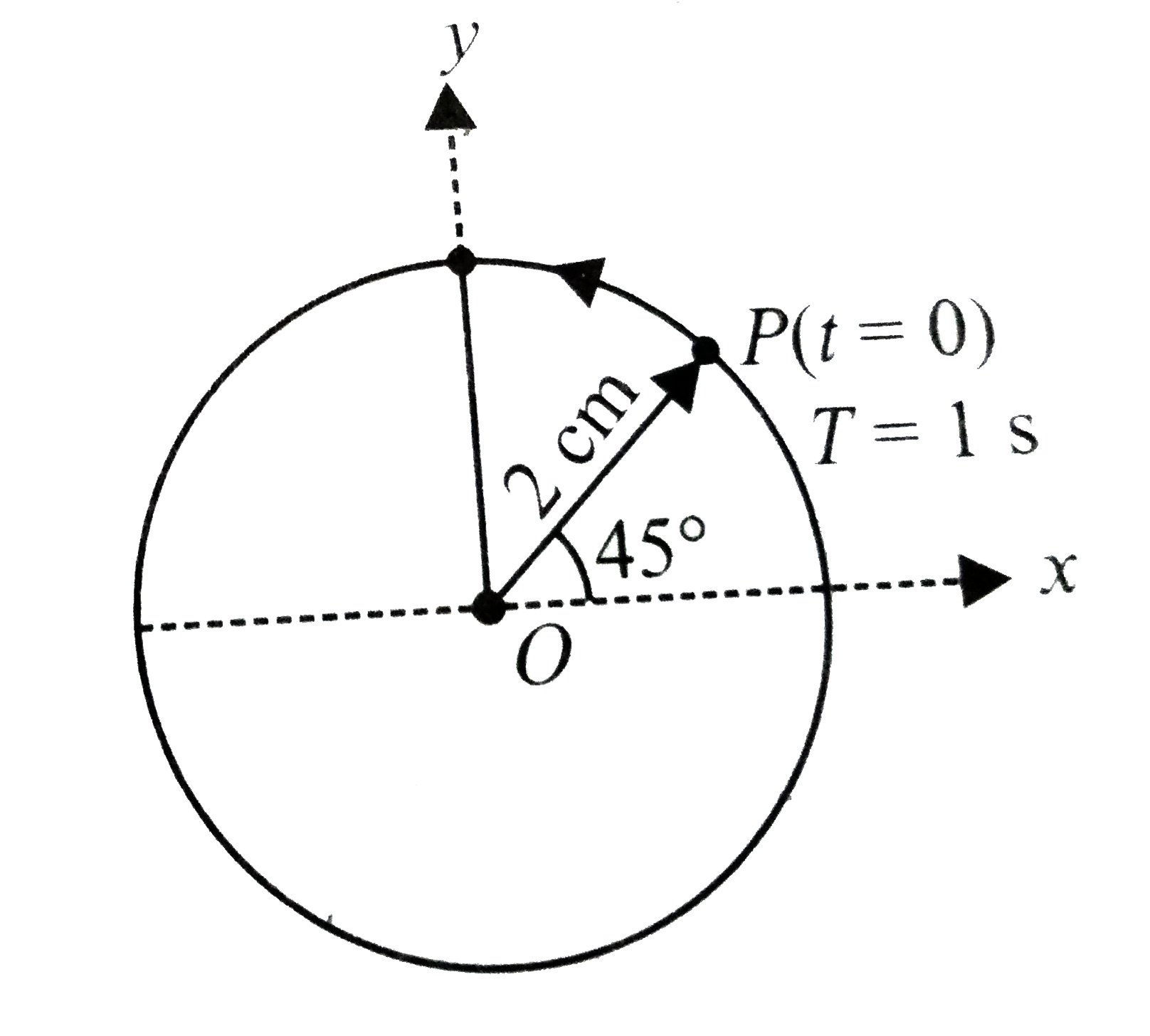
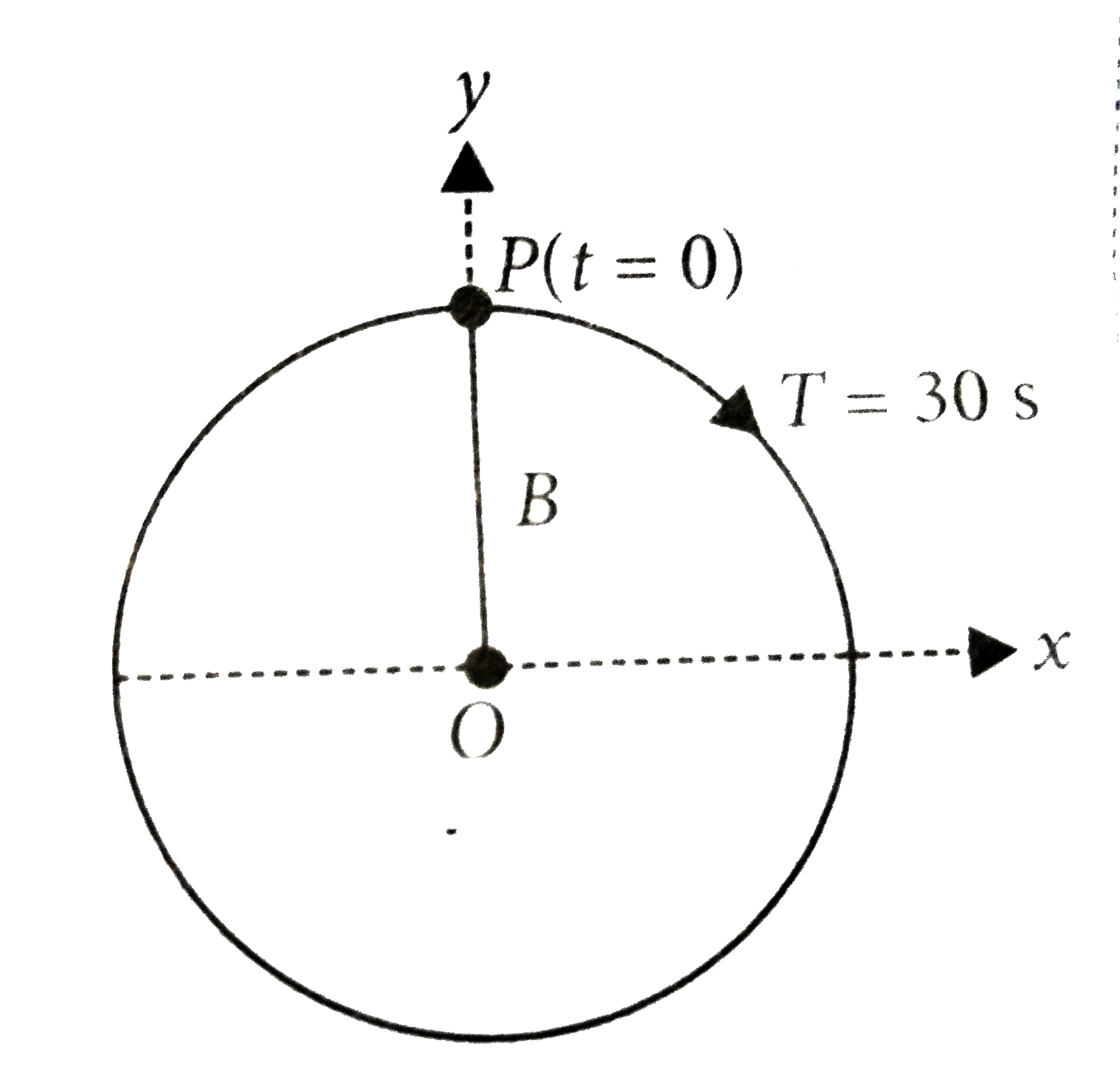
Figure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial positionn are indicated in the figure. The simple harmonic motion off the x-projection of the radius vector of the rotating particle P is
View SolutionA particle moves along the x-axis according to the equation x=asinωt+bcosωt. The motion is simple harmonic with
View Solution
