Radioactive element decays to form a stable nuclide, then the rate of decay of reactant (dNdt) will vary with time (t) as shown in figure.
_E01_063_O01.png)
_E01_063_O02.png)
_E01_063_O03.png)
_E01_063_O04.png)
The correct Answer is:D
To solve the problem regarding the decay of a radioactive element to form a stable nuclide, we will analyze the rate of decay over time and derive the necessary expressions step by step.
1. Understanding the Decay Process:
The decay of a radioactive element can be described by the equation:
N(t)=N0e−λt
where:
- N(t) is the number of undecayed nuclei at time t,
- N0 is the initial number of nuclei,
- λ is the decay constant,
- t is the time.
2. Differentiating the Decay Equation:
To find the rate of decay, we differentiate N(t) with respect to time t:
dNdt=ddt(N0e−λt)=−λN0e−λt
This indicates that the rate of decay is proportional to the number of undecayed nuclei present at that time.
3. Analyzing the Rate of Decay at Specific Times:
- At t=0:
dNdt∣∣∣t=0=−λN0e0=−λN0
- As t approaches infinity:
dNdt∣∣∣t→∞=−λN0e−λ⋅∞=0
4. Conclusion:
The rate of decay dNdt starts at −λN0 when t=0 and approaches 0 as t approaches infinity. This indicates that the decay rate decreases over time.
5. Choosing the Correct Option:
Based on the analysis, we can conclude that the rate of decay varies from −λN0 at t=0 to 0 as t approaches infinity. Thus, the correct option is:
- D: The rate of decay starts at −λN0 and decreases to 0.
The decay of a radioactive element can be described by the equation:
N(t)=N0e−λt
where:
- N(t) is the number of undecayed nuclei at time t,
- N0 is the initial number of nuclei,
- λ is the decay constant,
- t is the time.
To find the rate of decay, we differentiate N(t) with respect to time t:
dNdt=ddt(N0e−λt)=−λN0e−λt
This indicates that the rate of decay is proportional to the number of undecayed nuclei present at that time.
- At t=0:
dNdt∣∣∣t=0=−λN0e0=−λN0
- As t approaches infinity:
dNdt∣∣∣t→∞=−λN0e−λ⋅∞=0
The rate of decay dNdt starts at −λN0 when t=0 and approaches 0 as t approaches infinity. This indicates that the decay rate decreases over time.
Based on the analysis, we can conclude that the rate of decay varies from −λN0 at t=0 to 0 as t approaches infinity. Thus, the correct option is:
- D: The rate of decay starts at −λN0 and decreases to 0.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-02
19 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES
29 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
Nuclei of a radioactive element X are being produced at a constant rate K and this element decays to a stable nucleus Y with a decay constant λ and half-life T1/2. At the time t=0, there are N0nuclei of the element X.
The number NX of nuclei of X at time t=T1/2 is .
View SolutionNuclei of a radioactive element X are being produced at a constant rate K and this element decays to a stable nucleus Y with a decay constant λ and half-life T1/3. At the time t=0, there are N0nuclei of the element X.
The number NY of nuclei of Y at time t is .
View Solution
Knowledge Check
A radioactive element X with half life 2 h decays giving a stable element Y. After a time t, ratio of X and Y atoms is 1:16 .Time t is
A6 hB4 hC8 hD16 hWhen a certain radioactive elements decays, the amount at any time t can be calculated using the function E(t)=ae−t500 , where a is the original amound an t is the elapsed time in year.How many years would it take for an initial amount of 250 miligrams of this element to decay to 100 miligrams?
A125 yearsB200 yearsC458 yearsD496 years
Nucleus A decays into B with a decay constant λ1 and B further decays into C with a decay constant λ2 . Initially, at t = 0, the number of nuclei of A and B were 3N0 and N0 respectively. If at t = t0 number of nuclei of B becomes constant and equal to 2N0, then
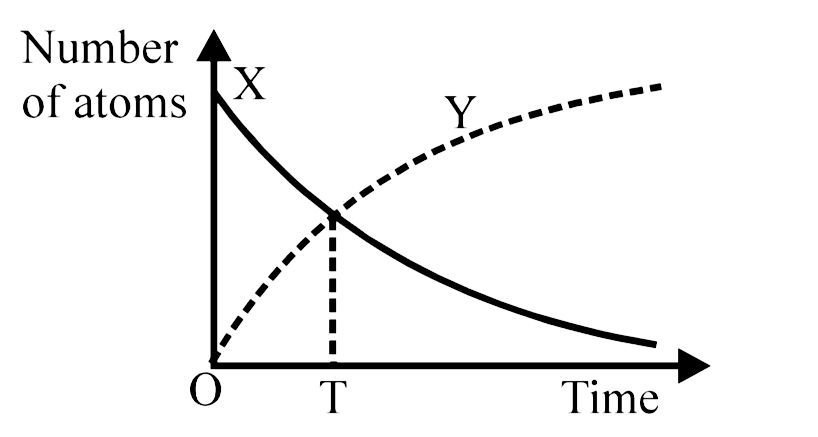
View SolutionThe graph represents the decay of a newly-prepared sample of radioactive nuclide X to a stable nuclide Y. The half-life of X is t. The growth curve for Y intersects the decay curve for X after time T. What is the time T ?
View SolutionA radioactive substance (parent) decays to its daughter element . The age of radioactive substance (t) is related to the daughter (d)/parent (p) ratio by the equation :
View SolutionTo determine the half life of a radioactive element , a student plot a graph of in ∣∣∣dN(t)dt∣∣∣ versus t , Here ∣∣∣dN(t)dt∣∣∣ is the rate of radiation decay at time t , if the number of radioactive nuclei of this element decreases by a factor of p after 4.16year the value of p is

View SolutionTo determine the half life of a radioactive element , a student plote a graph of in ∣∣∣dN(t)dt∣∣∣versust,Here∣∣∣dN(t)dt∣∣∣ is the rate of radioatuion decay at time t , if the number of radoactive nuclei of this element decreases by a factor of p after 4.16 year the value of p is

View SolutionA factory produces a radioactive substance A at a constant rate R which decays with a decay constant λ to form a stable substance. Find (a) the number of nuclei of A and (b) number of nuclei of B, at any time t assuming the production of A starts at t=0. (c ) Also, find out the maximum number of nuclei of A present at any time during its formation.
View Solution
