Use of dilution formula (M1V1=M2V2)

The correct Answer is:(##ALNNCCHMCTE01012_A01##)
Step by step video & image solution for Use of dilution formula (M_(1)V_(1) = M_(2) V_(2)) by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONCENTRATION TERMSBOOK - ALLENCHAPTER - CONCENTRATION TERMSEXERCISE - Exercise S - I
30 Videos
- CONCENTRATION TERMSBOOK - ALLENCHAPTER - CONCENTRATION TERMSEXERCISE - Exercise S - II
10 Videos
- CONCENTRATION TERMSBOOK - ALLENCHAPTER - CONCENTRATION TERMSEXERCISE - Previous
4 Videos
- ACIDIC STRENGTH & BASIC STRENGTHBOOK - ALLENCHAPTER - ACIDIC STRENGTH & BASIC STRENGTHEXERCISE - Exercise V
16 Videos
Similar Questions
V1mL of CH3COONa solution (of molarity M1) and V2mL of a HCl solution (of Molarity M2) are available ,Can the two be mixed to obtain a buffer solution? If Yes, what should be the mathematical condition relating M1,M2,V1&V2 for this?
View SolutionA: 50 ml, decinormal HCl when mixed with 50 ml, decinormal H2SO4, then normality of H+ ion in resultant solution is 0.1 N.
R: Here, MV=M1V1−M2V2
View SolutionAs part of his discovery of the neutron in 1932, James Chadwick determined the mass of the neutron (newly identified particle) by firing a beam of fast meutrons, all having the same speed, as two different targets and measuing the maximum recoil speeds of the target nuclei. The maximum speed arise when an elastic head-on collision occurs between a neutron and a stationary target nucleus. Represent the masses and final speeds of the two target nuclei as m1,v1,m2 and v2 and assume Newtonian mechanics applies. The neutron mass can be calculated from the equation:
mn=m1v1−m2v2v2−v1
Chadwick directed a beam of neutrons on paraffin, which contains hydrogen. The maximum speed of the protons ejected was found to be 3.3×107m/s. A second experiment was performed using neutrons from the same source and nitrogen nuclei as the target. The maximum recoil speed of the nitrogen nuclei was found to be 4.7×106m/s. The masses of a proton and a nitrogen nucleus were taken as 1u and 14u, respectively. What was Chadwick's value for the neutron mass?
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionTwo solution of H2SO4 of molarities x and y are mixed in the ratio of V1mL:V2mL to form a solution of molarity M1. If they are mixed in the ratio of V2mL:V1mL, they form a solution of molarity M2. Given V1/V2=xy>1andM1M2=54, then x:y is
View SolutionAt low pressure, the van der Waal's equation become :
(a)PVm=RT
(b)P(Vm−b)=RT
(c)(P+aV2M)Vm=RT
(d)P=RTVm+aV2m
View SolutionWhen a mass m is connected individually to two springs S1 and S2, the oscillation frequencies are v1 and v2. If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be

View SolutionTwo bodies having masses m1 and m2 and velocities v1 and v2 colide and form a composite system. If m1v1+m2v2=0(m1≠m2. The velocity of composite system will be
View SolutionTwo bodies having masses m1 and m2 and velocities v1 and v2 colide and form a composite system. If m1v1+m2v2=0(m1≠m2. The velocity of composite system will be
View SolutionA planet of mass M, has two natural satellites with masses m1 and m2. The radii of their circular orbits are R1 and R2 respectively. Ignore the gravitational force between the satellites. Define v1,L1,K1 and T1 to be, respectively, the orbital speed, angular momentum, kinetic energy and time period of revolution of satellite 1 , and v2,L2,K2 and T2 to be he corresponding quantities of satellite 2. Given m1/m2=2 and R1/R2=1/4, match the ratios in List-I to the numbers in List-II.
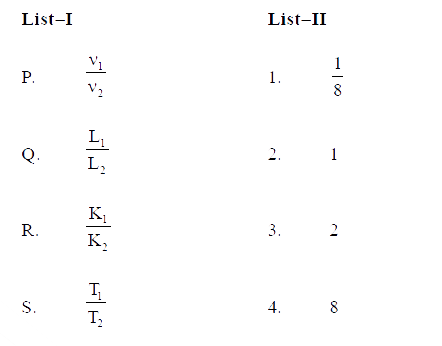
View Solution
