When a mass m is connected individually to two springs S1 and S2, the oscillation frequencies are v1 and v2. If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be

v1+v2
√v21+v22
(1v1+1v2)−1
√v21−v22

Consider the diagram, two springs can be considered as parallel.
Hence, keq=Equivalent spring constant
k1+k2
Time period of oscillatin of the spring block-system
T=2π√mkeq=2π√mk1+k2
⇒v=1T=12π×√k1+k2m
Equivalent oscillation frequency.
When the mass is connected to the two springs individually

v1=12π√k1m
v2=12π√k2m
From Eqs. (i),(ii) and (iii),
v=12π=[k1m+k2m]1/2 [from Eq. (i)]
12π[4π2v211+4π2v221]
[∵fromEq.(ii)k1m=4π2v21and fromEq.(iii),k2m=4π2v22]
=2π2π[v21+v22]1/2⇒v=√v21+v22]
Not Do not confuse with parallel and series combinations of springs.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:NCERT EXEMPLAR ENGLISHChapter:MOTION IN A STRAIGHT LINE Exercise:Very Short Answer Type Qns
Explore 14 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NCERT EXEMPLAR ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:Long answer type questions
Explore 12 Videos
Similar Questions
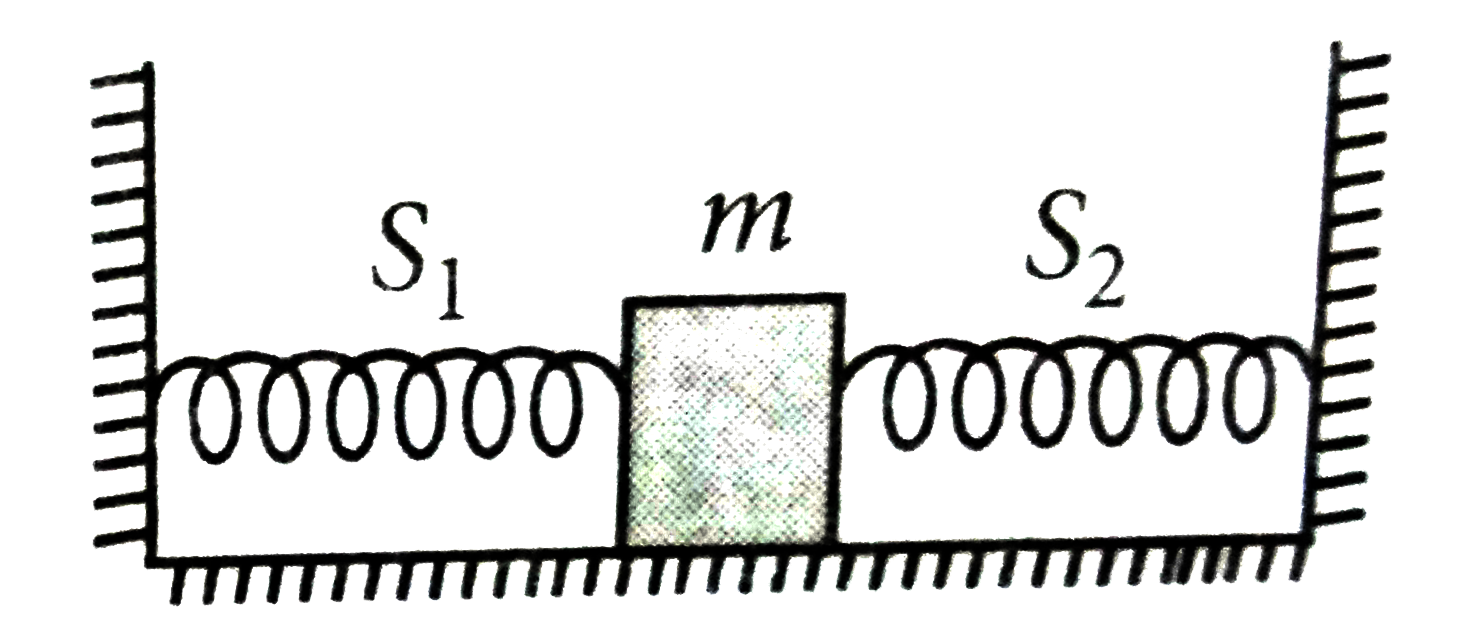
When a mass m is connected individually to two springs S1andS2, the oscillation frequencies are υ1andυ2. If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be
View SolutionFour spring connect with mass as shown in figure. Find frequency of S.H.M.

View Solution
Knowledge Check
When a body is suspended from two light springs separately, the periods of vertical oscillations are T1 and T2. When the same body is suspended from the two spring connected in series, the period will be
AT=T1+T2B1T=1T1+1T2CT2=T21+T22D1T2=1T21+1T2A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
Four spring connect with mass as shown in figure. Find frequency of S.H.M.

View SolutionA mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is

View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionA very light rod of length l pivoted at O is connected with two springs of stiffness k1 & k2 at a distance of a & l from the pivot respectively. A block of mass ma attached with the spring k2 is kept on a smooth horizontal surface. Find the angular frequency of small oscillation of the block m.
_S01_031_Q01.png)
View SolutionWhen a block of mass m is suspended separately by two different springs have time period t1 and t2. If same mass is connected to parallel combination of both springs, then its time period is given by :-
View SolutionThe frequency of oscillation of amass m suspended by a spring is v1. If length of spring is cut to one third then the same mass oscillations with frequency v2. Then
View Solution