Let P be an interior point of a triangle ABC , Let Q and R be the reflections of P in AB and AC , respectively if Q .A , R are collinear then equals -
The correct Answer is:C
To solve the problem, we need to analyze the given geometric configuration involving triangle ABC and the interior point P. Here’s a step-by-step solution:
Step 1: Understand the Configuration
- We have triangle ABC with point P inside it.
- Points Q and R are the reflections of point P across sides AB and AC, respectively.
Step 2: Draw the Diagram
- Draw triangle ABC.
- Mark point P inside the triangle.
- Reflect point P across line AB to get point Q.
- Reflect point P across line AC to get point R.
Step 3: Analyze the Collinearity Condition
- The problem states that points Q, A, and R are collinear.
- For three points to be collinear, the angles formed at point A must satisfy certain conditions.
Step 4: Use Angle Relationships
- Let ∠PAB=θ and ∠PAC=ϕ.
- When P is reflected to Q and R, the angles change:
- The angle ∠QAB=θ
- The angle ∠RAC=ϕ
Step 5: Set Up the Equation
- Since Q, A, and R are collinear, the angles around point A must sum to 180∘:
∠QAP+∠RAP=180∘
- This can be expressed as:
θ+ϕ+θ+ϕ=180∘
Simplifying gives:
2θ+2ϕ=180∘
Dividing by 2:
θ+ϕ=90∘
Step 6: Conclusion
- The angle A in triangle ABC is given by:
∠A=θ+ϕ=90∘
- Therefore, the measure of angle A is 90∘.
Final Answer
∠A=90∘
---
- We have triangle ABC with point P inside it.
- Points Q and R are the reflections of point P across sides AB and AC, respectively.
- Draw triangle ABC.
- Mark point P inside the triangle.
- Reflect point P across line AB to get point Q.
- Reflect point P across line AC to get point R.
- The problem states that points Q, A, and R are collinear.
- For three points to be collinear, the angles formed at point A must satisfy certain conditions.
- Let ∠PAB=θ and ∠PAC=ϕ.
- When P is reflected to Q and R, the angles change:
- The angle ∠QAB=θ
- The angle ∠RAC=ϕ
- Since Q, A, and R are collinear, the angles around point A must sum to 180∘:
∠QAP+∠RAP=180∘
- This can be expressed as:
θ+ϕ+θ+ϕ=180∘
Simplifying gives:
2θ+2ϕ=180∘
Dividing by 2:
θ+ϕ=90∘
- The angle A in triangle ABC is given by:
∠A=θ+ϕ=90∘
- Therefore, the measure of angle A is 90∘.
∠A=90∘
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 3
10 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 4
10 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Race 21
14 Videos
- LOGARITHMSBOOK - ALLENCHAPTER - LOGARITHMSEXERCISE - All Questions
92 Videos
- SEQUENCE AND PROGRESSIONBOOK - ALLENCHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)
12 Videos
Similar Questions
If points Q and R reflections of point P(−3, 4) in X and Y axes respectively, what is QR ?
View SolutionIn a triangle ABC , let P and Q be points on AB and AC respectively such that PQ∣∣BC . Prove that the median AD bisects PQ.
View SolutionIn the given triangle P, Q and R are the mid points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

View SolutionIf p , q , r are the legths of the internal bisectors of angles A ,B , C respectively of a !ABC , then area of ABC

View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
View SolutionLet P be the point (3, 2). Let Q be the reflection of P about the x-axis. Let R be the reflection of Q about the line y=−x and let S be the reflection of R through the origin, PQRS is a convex quadrilateral . Find the area of PQRS.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
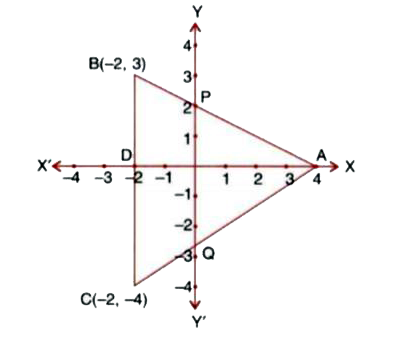
Find the length of AB and AC.
View SolutionIn triangle PQR, if PQ=RQ and L, M and N are the mid-points of the sides PQ, QR and RP respectively. Prove that LN=MN.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
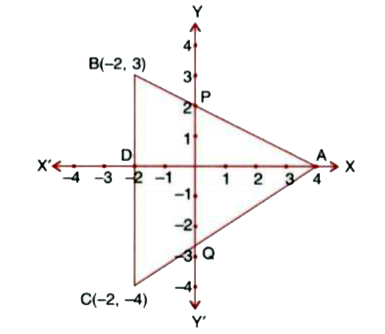
Write the co-ordinates of A.
View SolutionIn △PQR , right-angled at Q, PQ=3cm and PR=6cm . Determine ∠P and ∠R .
View Solution
