A motor boat of mass m moves along a lake with velocity V0. At t=0, the engine of the boat is shut down. Magnitude of resistance force offered to the boat is equal to rV. (V is instantaneous speed). What is the total distance covered till it stops completely? [Hint: F(x)=mVdVdx=−rV]
mV0/r
3mV0/2r
mV0/2r
2mV0/r
To solve the problem of the motorboat coming to a stop due to resistance, we will follow these steps:
1. Understand the Forces Acting on the Boat:
The resistance force acting on the boat is given as F=−rV, where V is the instantaneous speed of the boat. The negative sign indicates that the force is acting in the opposite direction to the motion of the boat.
2. Apply Newton's Second Law:
According to Newton's second law, the force can also be expressed as:
F=m⋅a
where m is the mass of the boat and a is its acceleration. Since the resistance force is the only force acting on the boat after the engine is shut down, we can equate the two expressions for force:
m⋅a=−rV
3. Relate Acceleration to Velocity and Distance:
We know that acceleration a can be expressed in terms of velocity V and distance s as:
a=VdVds
Substituting this into our force equation gives:
m⋅VdVds=−rV
4. Simplify the Equation:
We can cancel V from both sides (assuming V≠0):
mdVds=−r
Rearranging this gives:
ds=−mrdV
5. Integrate Both Sides:
We need to integrate both sides to find the total distance s covered by the boat until it comes to a stop. The limits for V will be from V0 (initial velocity) to 0 (final velocity):
∫s0ds=−mr∫0V0dV
6. Perform the Integration:
The left side integrates to s and the right side becomes:
s=−mr(V)0V0=−mr(0−V0)=mV0r
7. Final Result:
Thus, the total distance covered by the boat until it stops completely is:
s=mV0r
The resistance force acting on the boat is given as F=−rV, where V is the instantaneous speed of the boat. The negative sign indicates that the force is acting in the opposite direction to the motion of the boat.
According to Newton's second law, the force can also be expressed as:
F=m⋅a
where m is the mass of the boat and a is its acceleration. Since the resistance force is the only force acting on the boat after the engine is shut down, we can equate the two expressions for force:
m⋅a=−rV
We know that acceleration a can be expressed in terms of velocity V and distance s as:
a=VdVds
Substituting this into our force equation gives:
m⋅VdVds=−rV
We can cancel V from both sides (assuming V≠0):
mdVds=−r
Rearranging this gives:
ds=−mrdV
We need to integrate both sides to find the total distance s covered by the boat until it comes to a stop. The limits for V will be from V0 (initial velocity) to 0 (final velocity):
∫s0ds=−mr∫0V0dV
The left side integrates to s and the right side becomes:
s=−mr(V)0V0=−mr(0−V0)=mV0r
Thus, the total distance covered by the boat until it stops completely is:
s=mV0r
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 19
1 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Race 21
5 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
A motor boat of mass m moves along a lake with velocity v0. At t = 0, the engine of the boat is shut down. Resistance offered to the boat is equal to σv2. Then distance covered by the boat when its velocity becomes v0/2 is
View SolutionA motor boat of mass m moves along a lake with velocity V0. At the moment t=0 the engine of the boat is shut down. Assuming the resistance of water is proportional to the velocity of the boat →F=−r→v
Q. How long the motor boat with the shut down engine.
View SolutionA motor boat of mass m moves along a lake with velocity V0. At the moment t=0 the engine of the boat is shut down. Assuming the resistance of water is proportional to the velocity of the boat →F=−r→v
Q. The velocity (v) of the motor boat as a function of the distance (s) covered with the shutdown engine is
View SolutionThe force of resistance encountered by water on a motor boat of mass m going in still water with velocity v is proportional to the velocity v. At t=0 when its velocity is v0, then engine shuts off. Find an expression for the position of motor boat at time t and also the distance travelled by the boat before it comes to rest. Take the proportionality constant as k>0.
View SolutionA particle of mass m moves on a straight line with its velocity varying with the distance travelled according to the equation v=a√x, where a is a constant. Find the total work done by all the forces during a displacement from x=0→x=d.
View SolutionA particle of mass m moves on a straight line with its velocity varying with the distance travelled according to the equation v=a√x, wher ea is a constant. Find the total work done by all the forces during a displacement from x=0→x=d.
View SolutionA particle of mass m moves on a straight line with its velocity varying with the distance travelled according to the equation v=a√x, where a is a constant. Find the total work done by all the forces during a displacement from x=0→x=d.
View SolutionTwo blocks A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a spring. A third block C of mass m moves with a velocity v0 along the line joing A and B and collides elastically with A, as shown in figure. At a certain instant of time t0 after collision, it is found that the instantaneous velocities of A and B are the same. Further, at this instant the compression of the spring is found to be x0. Determine (i) the common velocity of A and B at time t0, and (ii) the spring constant.
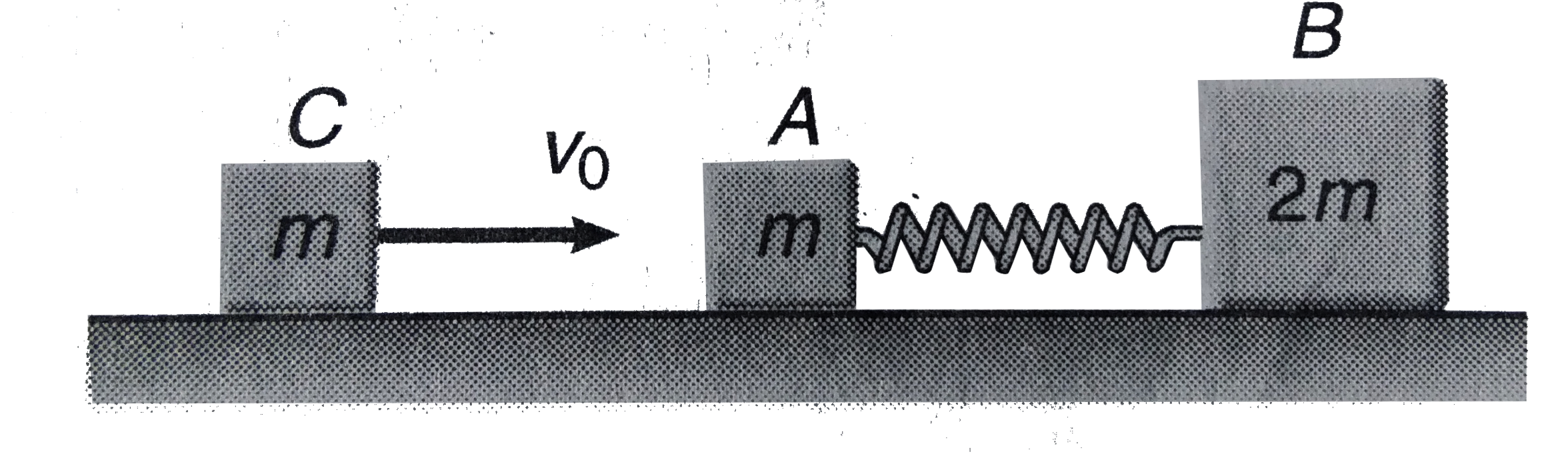
View SolutionA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
View SolutionA particle of mass m moves with a variable velocity v, which changes with distance covered x along a straight line as v=k√x, where k is a positive constant. The work done by all the forces acting on the particle, during the first t seconds is
View Solution
