A motor boat of mass m moves along a lake with velocity v0. At t = 0, the engine of the boat is shut down. Resistance offered to the boat is equal to σv2. Then distance covered by the boat when its velocity becomes v0/2 is
3mv02σ
v0mln22σ
2mIn2σ
mIn2σ
The correct Answer is:D
To solve the problem, we need to find the distance covered by a motorboat when its velocity decreases from v0 to v02 after the engine is shut down. The resistance offered to the boat is proportional to the square of its velocity, given by σv2.
1. Understanding Forces:
When the engine is shut down, the only force acting on the boat is the resistive force, which is given by Fresistance=σv2. According to Newton's second law, we have:
F=ma=mdvdt
Thus, we can write:
mdvdt=−σv2
The negative sign indicates that the force is acting in the opposite direction of the motion.
2. Changing Variables:
We can express dvdt in terms of displacement s using the chain rule:
dvdt=dvds⋅dsdt=vdvds
Therefore, substituting this into our equation gives:
mvdvds=−σv2
3. Simplifying the Equation:
We can cancel v from both sides (assuming v≠0):
mdvds=−σv
Rearranging gives:
dvds=−σmv
4. Separating Variables:
We can separate the variables to integrate:
dvv=−σmds
5. Integrating:
Now we integrate both sides. The limits for v are from v0 to v02 and for s from 0 to s:
∫v02v01vdv=−σm∫s0ds
This gives:
ln(vv0)∣∣∣v02v0=−σms
Evaluating the left side:
ln⎛⎝v02v0⎞⎠=ln(12)=−ln(2)
Thus, we have:
−ln(2)=−σms
6. Solving for Distance s:
Rearranging gives:
s=mln(2)σ
Final Answer:
The distance covered by the boat when its velocity becomes v02 is:
s=mln(2)σ
When the engine is shut down, the only force acting on the boat is the resistive force, which is given by Fresistance=σv2. According to Newton's second law, we have:
F=ma=mdvdt
Thus, we can write:
mdvdt=−σv2
The negative sign indicates that the force is acting in the opposite direction of the motion.
We can express dvdt in terms of displacement s using the chain rule:
dvdt=dvds⋅dsdt=vdvds
Therefore, substituting this into our equation gives:
mvdvds=−σv2
We can cancel v from both sides (assuming v≠0):
mdvds=−σv
Rearranging gives:
dvds=−σmv
We can separate the variables to integrate:
dvv=−σmds
Now we integrate both sides. The limits for v are from v0 to v02 and for s from 0 to s:
∫v02v01vdv=−σm∫s0ds
This gives:
ln(vv0)∣∣∣v02v0=−σms
Evaluating the left side:
ln⎛⎝v02v0⎞⎠=ln(12)=−ln(2)
Thus, we have:
−ln(2)=−σms
Rearranging gives:
s=mln(2)σ
The distance covered by the boat when its velocity becomes v02 is:
s=mln(2)σ
Similar Questions
A motor boat of mass m moves along a lake with velocity V0. At t=0, the engine of the boat is shut down. Magnitude of resistance force offered to the boat is equal to rV. (V is instantaneous speed). What is the total distance covered till it stops completely? [Hint: F(x)=mVdVdx=−rV]
View SolutionA motor boat of mass m moves along a lake with velocity V0. At the moment t=0 the engine of the boat is shut down. Assuming the resistance of water is proportional to the velocity of the boat →F=−r→v
Q. The velocity (v) of the motor boat as a function of the distance (s) covered with the shutdown engine is
View SolutionA motor boat of mass m moves along a lake with velocity V0. At the moment t=0 the engine of the boat is shut down. Assuming the resistance of water is proportional to the velocity of the boat →F=−r→v
Q. How long the motor boat with the shut down engine.
View SolutionA body of mass m is thrown straight up with velocity v0(v0<<ve) Find the velocity v with which the body comes down if the air drag equals kv2, where k is a positive constant and v is the velocity of the body.
View SolutionA particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
total distance covered by the particle is
View SolutionThe force of resistance encountered by water on a motor boat of mass m going in still water with velocity v is proportional to the velocity v. At t=0 when its velocity is v0, then engine shuts off. Find an expression for the position of motor boat at time t and also the distance travelled by the boat before it comes to rest. Take the proportionality constant as k>0.
View SolutionA particle of mass m is moving with a uniform velocity v1. It is given an impulse such that its velocity becomes v2. The impulse is equal to
View SolutionA ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is
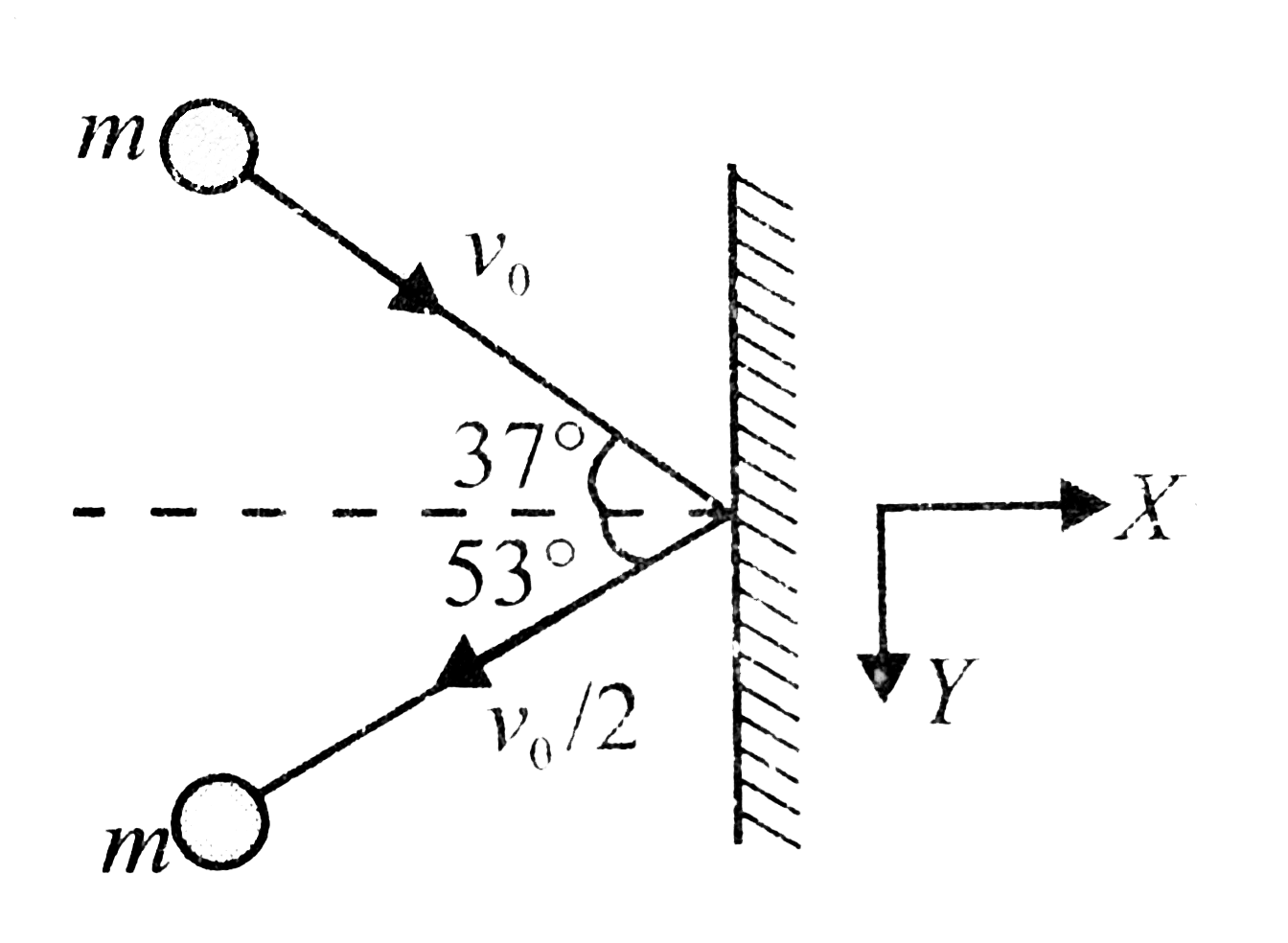
View SolutionA particle of mass m is moving with constant velocity v0 along the line y=b. At time t=0 it was at the point (0,b). At time t=bv0, the

View SolutionA man is rowing a boat with a constant velocity v0 in a river. The contact area of boat is 'A' and coefficient of viscosity is η. The depth of river is 'D' . Find the force required to row the boat.
View Solution
