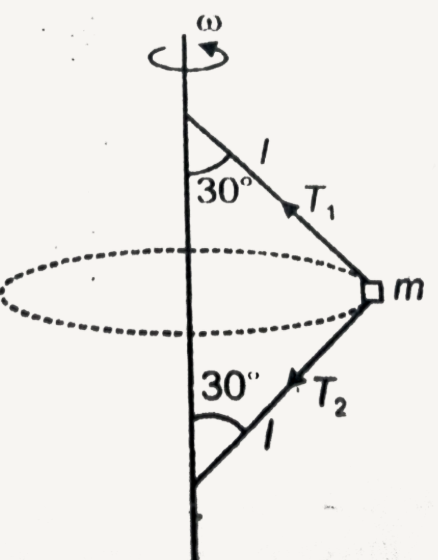
A particle P of mass m is attached to a vertical axis by two strings AP and BP of length l each. The separation AB=l. P rotates around the axis with an angular velocity ω. The tensions in the two strings are T1andT2
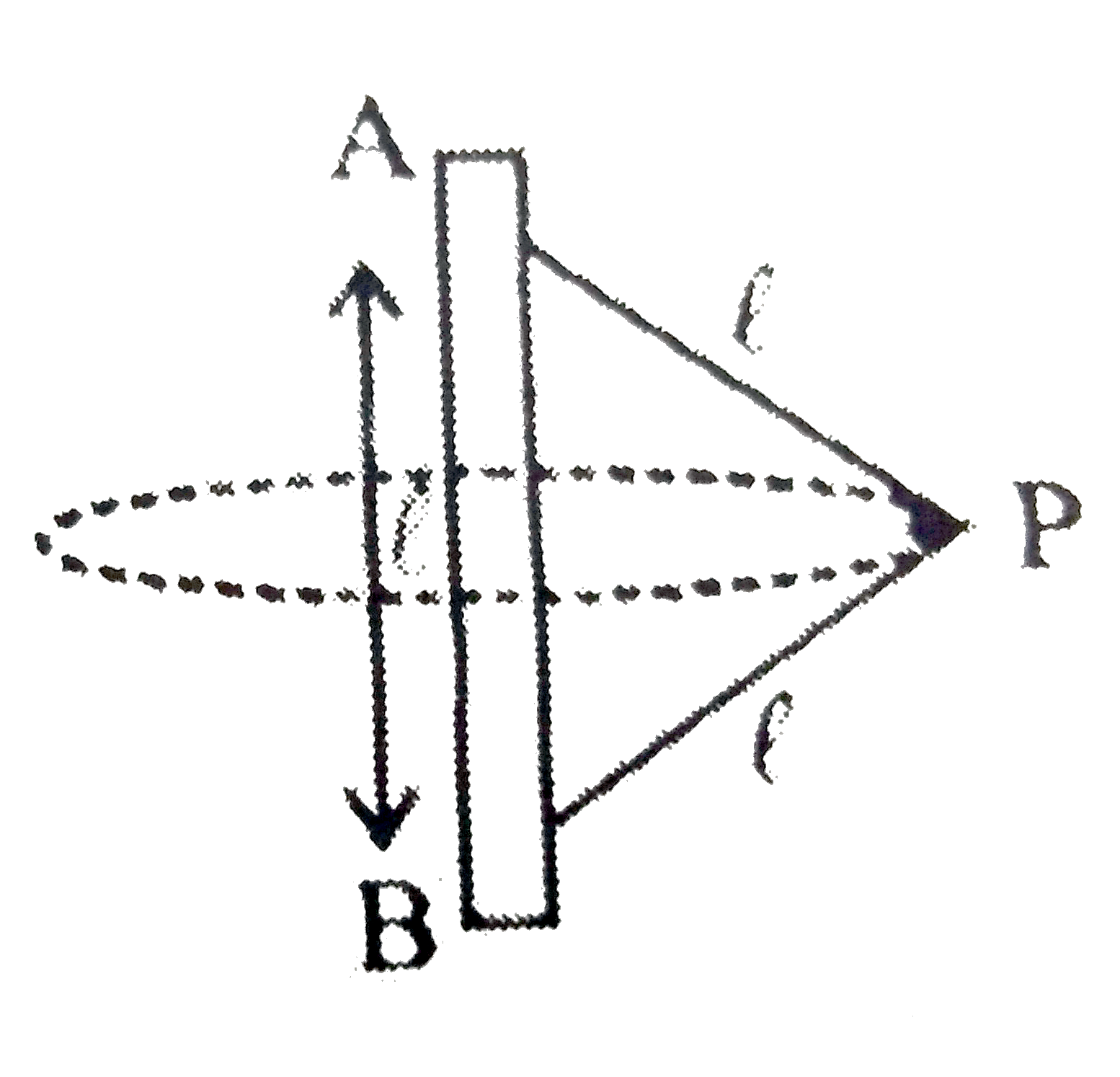
T1=T2
T1+T2=mω2l
T1−T2=2mg
BP will remain taut only if ω≥√2gl
The correct Answer is:B, C, D
Step by step video & image solution for A particle P of mass m is attached to a vertical axis by two strings AP and BP of length l each. The separation AB=l. P rotates around the axis with an angular velocity omega. The tensions in the two strings are T_(1) and T_(2) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - Martrix match
1 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(O-2)
7 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(O-1)
22 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
Similar Questions
A particle of mass m is attached to a vertical rod with two inextensible strings AO and BO of equal lengths l. Distance between A and B is also l. The setup is rotated with angular speed ω with rod as the axis.
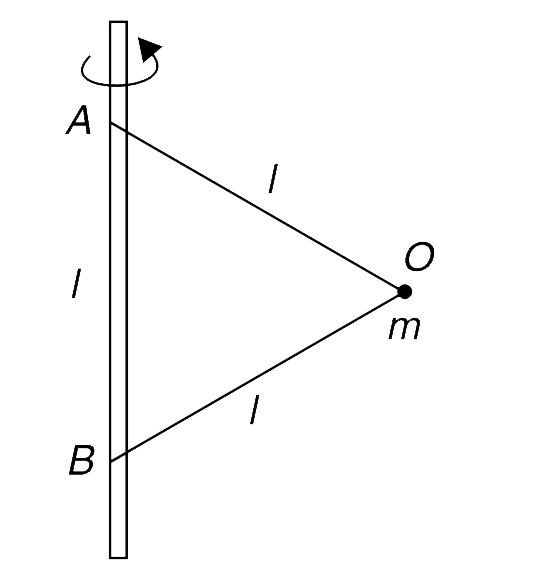
View SolutionA particle of mass m is attached to the celling of a cabin with an inextensible light string of length l. The cabin is moving upward with an acceleration a . The particle is taken to a position such that string makes an angle θ with vertical. When string becomes vertical, find the tension in the string.

View Solution
Knowledge Check
A mass is supported on a frictionless horizontal surface. It is attached to a string and rotates about a fixed centre with a angular velocity ω0. If the length of the string and angular velocity are doubled, the tension in the string which was initially T0 is now
AT0BT0/2C4T0D8T0
Three balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O.find the tensions .
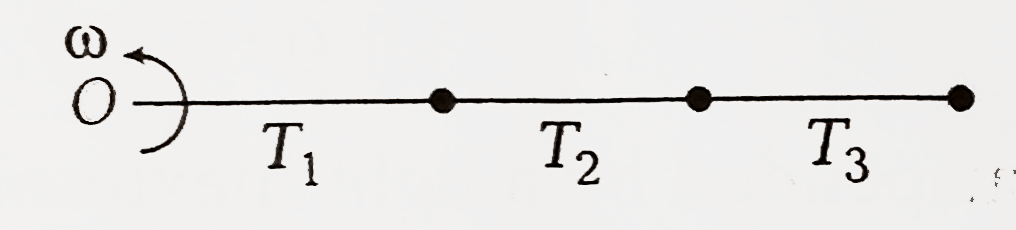
View SolutionA string has a linear mass density μ. The ends of the string are joined to form a closed loop and is given the shape of a circular ring of radius R. this ring is now rotated about its axis with an angular velocity ω
Q. The tension developed in the string is
View SolutionIn the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity ω1 when
View SolutionA particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v0 to complete the vertical circle. The tension in the string when it becomes horizontal is
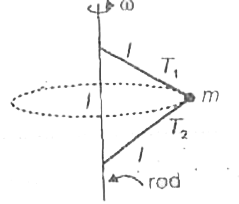
View SolutionA particle of mass m is whirled in horizontal circle with the help of two threads of length l each as shown in figure . Angular velocity equals ω, then
T1 equals
View SolutionA particle of mass m is whirled in horizontal circle with the help of two threads of length l each as shown in figure . Angular velocity equals ω, then
View SolutionA particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u. The tension in the string is T and acceleration of the particle is a at any position then T. a' is positive at the lowest point for
View Solution
