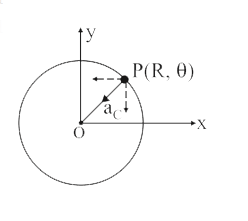
For a particle in uniform circular motion , the acceleration →a at a point p(R,θ) on the circle of radiu R is ( Here θ is measured from the x−aξs )
v2Rˆi+v2Rjˆ
−v2Rcosθˆi+v2Rsinθjˆ
−v2Rsinθˆi+v2Rcosθjˆ
−v2Rcosθˆi−v2Rsinθjˆ
The correct Answer is:D
To solve the problem regarding the acceleration of a particle in uniform circular motion at a point P(R,θ) on the circle of radius R, we can follow these steps:
1. Understanding Uniform Circular Motion:
- In uniform circular motion, a particle moves in a circular path with constant speed. The direction of the velocity vector changes continuously, which results in an acceleration directed towards the center of the circle.
2. Identifying the Radius and Angle:
- The particle is located at point P on the circle with radius R and angle θ measured from the positive x-axis.
3. Expression for Centripetal Acceleration:
- The magnitude of the centripetal acceleration a for uniform circular motion is given by:
a=v2R
where v is the constant speed of the particle.
4. Direction of Acceleration:
- The acceleration vector points towards the center of the circle. At point P, we can resolve this acceleration into its components along the x-axis and y-axis.
5. Resolving Acceleration into Components:
- The acceleration vector →a can be expressed in terms of its components:
- The x-component of the acceleration is directed towards the center and can be expressed as:
ax=−acos(θ)=−v2Rcos(θ)
- The y-component of the acceleration is also directed towards the center and can be expressed as:
ay=−asin(θ)=−v2Rsin(θ)
6. Writing the Acceleration Vector:
- Combining both components, we can write the acceleration vector →a in vector form:
→a=ax^i+ay^j=−v2Rcos(θ)^i−v2Rsin(θ)^j
7. Final Result:
- Therefore, the acceleration vector at point P(R,θ) is:
→a=−v2Rcos(θ)^i−v2Rsin(θ)^j
- In uniform circular motion, a particle moves in a circular path with constant speed. The direction of the velocity vector changes continuously, which results in an acceleration directed towards the center of the circle.
- The particle is located at point P on the circle with radius R and angle θ measured from the positive x-axis.
- The magnitude of the centripetal acceleration a for uniform circular motion is given by:
a=v2R
where v is the constant speed of the particle.
- The acceleration vector points towards the center of the circle. At point P, we can resolve this acceleration into its components along the x-axis and y-axis.
- The acceleration vector →a can be expressed in terms of its components:
- The x-component of the acceleration is directed towards the center and can be expressed as:
ax=−acos(θ)=−v2Rcos(θ)
- The y-component of the acceleration is also directed towards the center and can be expressed as:
ay=−asin(θ)=−v2Rsin(θ)
- Combining both components, we can write the acceleration vector →a in vector form:
→a=ax^i+ay^j=−v2Rcos(θ)^i−v2Rsin(θ)^j
- Therefore, the acceleration vector at point P(R,θ) is:
→a=−v2Rcos(θ)^i−v2Rsin(θ)^j
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(O-2)
7 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
Similar Questions
For a particle in uniform circular motion the acceleration →a at a point P(R,θ) on the circle of radius R is : ( here θ is measured from the x- axis )
View SolutionFor a particle in uniform circular motion the acceleration a at a point P(R,θ) on the circle of radius R is (here 'v' is the speed of the particle and θ is measured from the x-axis)
View SolutionA particle describes uniform circular motion. Find the torque on it about the centre of the circle.
View SolutionA particle undergoes uniform circular motion. About which point on the plane of the circle, will the angular momentum of the particle remain conserved?
View SolutionThe acceleration of an object moving in a circle of radius R with uniform speed v is
View SolutionWrite the formula for the area of a sector of angle θ (in degrees) of a circle of radius r .
View SolutionCentripetal acceleration of a particle of mass m moving in a circle of radius r is 4/r2. What is the angular momentum of the particle ?
View SolutionA particle in a circular motion covers a distance of 0.5 πr where r is the radius of the circular path. What is the angular displacement ?
View SolutionSTATEMENT -1 : In non - uniform circular motion acceleration of a particles is along the tangent of the circle .
STATEMENT -2 : In uniform circular motion acceleration of a particle is zero .
STATEMENT -3 : In no - uniform circular motion acceleration of a particle is towards the centre of the circle.
View SolutionIn a non - uniform circular motaion the ratio of tangential to radial acceleration is (where, r= radius of circle, v= speed of the particle, α= angular acceleration)
View Solution
