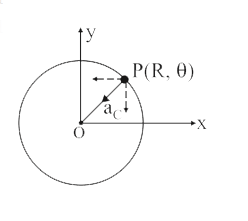
For a particle in uniform circular motion the acceleration →a at a point P(R,θ) on the circle of radius R is : ( here θ is measured from the x- axis )
−v2Rcosθˆi+v2Rsinθˆj
−v2Rsinθˆi+v2Rcosθˆj
−v2Rcosθhai−v2Rsinθˆj
v2Rˆi+v2Rˆj
The correct Answer is:D
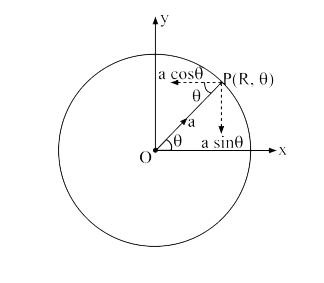
For a particle in uniform circular motion, acceleration a=v2R is toward the centre. From figure, we have −a=−acosθˆi−asinθˆj⇒−a=−v2Rcosθˆi−v2Rsinθˆj
Topper's Solved these Questions
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Advanced (Archive)
19 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - Level -1
140 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
Similar Questions
For a particle in uniform circular motion , the acceleration →a at a point p(R,θ) on the circle of radiu R is ( Here θ is measured from the x−aξs )
View SolutionFor a particle in uniform circular motion the acceleration a at a point P(R,θ) on the circle of radius R is (here 'v' is the speed of the particle and θ is measured from the x-axis)
View SolutionA particle describes uniform circular motion. Find the torque on it about the centre of the circle.
View SolutionA particle in a circular motion covers a distance of 0.5 πr where r is the radius of the circular path. What is the angular displacement ?
View SolutionA particle undergoes uniform circular motion. About which point on the plane of the circle, will the angular momentum of the particle remain conserved?
View SolutionFor a curved track of radius R, banked at angle θ
View SolutionSTATEMENT -1 : In non - uniform circular motion acceleration of a particles is along the tangent of the circle .
STATEMENT -2 : In uniform circular motion acceleration of a particle is zero .
STATEMENT -3 : In no - uniform circular motion acceleration of a particle is towards the centre of the circle.
View SolutionWrite the formula for the area of a sector of angle θ (in degrees) of a circle of radius r .
View SolutionCentripetal acceleration of a particle of mass m moving in a circle of radius r is 4/r2. What is the angular momentum of the particle ?
View SolutionIn a non - uniform circular motaion the ratio of tangential to radial acceleration is (where, r= radius of circle, v= speed of the particle, α= angular acceleration)
View Solution