Two astronauts A and B connected with a rope stay stationary in free space relative to their spaceship. Mass of A is more than that of B and the rope is straight. Astronaut A statas pulling the rope but astronaut B does not. If you were the third astronaut in the spaceship, what do you observe?
Astronaut B accelerates towards A and A remains stateionery.
Both accelerate towards each other with equal accelerations of equal modulus.
Both accelerate towards each other but acceleration of B is greater than that of A.
Both accelerate to wards each other but acceleration of B is smaller than that of A.
The correct Answer is:C
To solve the problem, we need to analyze the situation involving the two astronauts A and B, who are connected by a rope in free space. Here’s a step-by-step breakdown of the scenario:
Step 1: Understand the Forces Acting on the Astronauts
- Astronaut A has a greater mass (mA) than Astronaut B (mB).
- When A starts pulling the rope, a tension (T) is created in the rope.
- According to Newton's third law, the tension in the rope will act equally on both astronauts.
Step 2: Apply Newton's Second Law
- For Astronaut A:
F=mA⋅aA⟹T=mA⋅aA(1)
- For Astronaut B:
F=mB⋅aB⟹T=mB⋅aB(2)
Step 3: Relate the Accelerations
- From equations (1) and (2), we can express the accelerations in terms of tension:
aA=TmA(3)
aB=TmB(4)
Step 4: Compare the Accelerations
- Since mA > mB, it follows that:
aA<aB
- This means that Astronaut B will accelerate more than Astronaut A.
Step 5: Conclusion
- As a result, when Astronaut A pulls the rope, Astronaut B will accelerate toward A while A remains relatively stationary. Therefore, from the perspective of the third astronaut in the spaceship, you will observe that Astronaut B moves towards Astronaut A.
Final Answer
- The correct observation is that Astronaut B accelerates toward A while A remains stationary.
---
- Astronaut A has a greater mass (mA) than Astronaut B (mB).
- When A starts pulling the rope, a tension (T) is created in the rope.
- According to Newton's third law, the tension in the rope will act equally on both astronauts.
- For Astronaut A:
F=mA⋅aA⟹T=mA⋅aA(1)
- For Astronaut B:
F=mB⋅aB⟹T=mB⋅aB(2)
- From equations (1) and (2), we can express the accelerations in terms of tension:
aA=TmA(3)
aB=TmB(4)
- Since mA > mB, it follows that:
aA<aB
- This means that Astronaut B will accelerate more than Astronaut A.
- As a result, when Astronaut A pulls the rope, Astronaut B will accelerate toward A while A remains relatively stationary. Therefore, from the perspective of the third astronaut in the spaceship, you will observe that Astronaut B moves towards Astronaut A.
- The correct observation is that Astronaut B accelerates toward A while A remains stationary.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (O-2)
31 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JM)
6 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (S-2)
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
Similar Questions
Two astronauts are floating in gravitational free space after having lost contact with their spaceship. The two will:
View SolutionTwo astronauts are floating in gravitational free space after having lost contanct with their spaceship. The two will:
View SolutionA cord of length 64m is used to connected a 100kg astronaut to spaceship whose mass is much larger than that of the astronuat. Estimate the value of the tension in the cord. Assume that the spaceship is orbiting near earth surface. Assume that the spaceship and the astronaut fall on a straight line from the earth centre. the radius of the earth is 6400km.
View SolutionTwo fat astronauts each of mass 120 kg are travelling in a closed spaceship moving at a speed of 15 km/s in the outer space far removed from tall other material objects. The total mass of the spaceship and its contents including the astronauts is 660 kg. If the astronauts do slimming exercise and thereby reduce their masses to 90 kg each, with what velocity will spaceship move?
View SolutionTwo astronauts have deserted their spaceship in a region of space far from the gravitational attraction of any other body. Each has a mass of 100kg and they are 100m apart. They are initially at rest relative to one another. How long will it be before the gravitational attraction brings them 1cm closer together?
View SolutionTwo particles of equal mass are connected to a rope AB of negligible mass, such that one is at end A and the other dividing the length of the rope in the ratio 1:2 from A.The rope is rotated about end B is a horizontal plane. Ratio of the tensions in the smaller part to the other is (ignore effect of gravity)
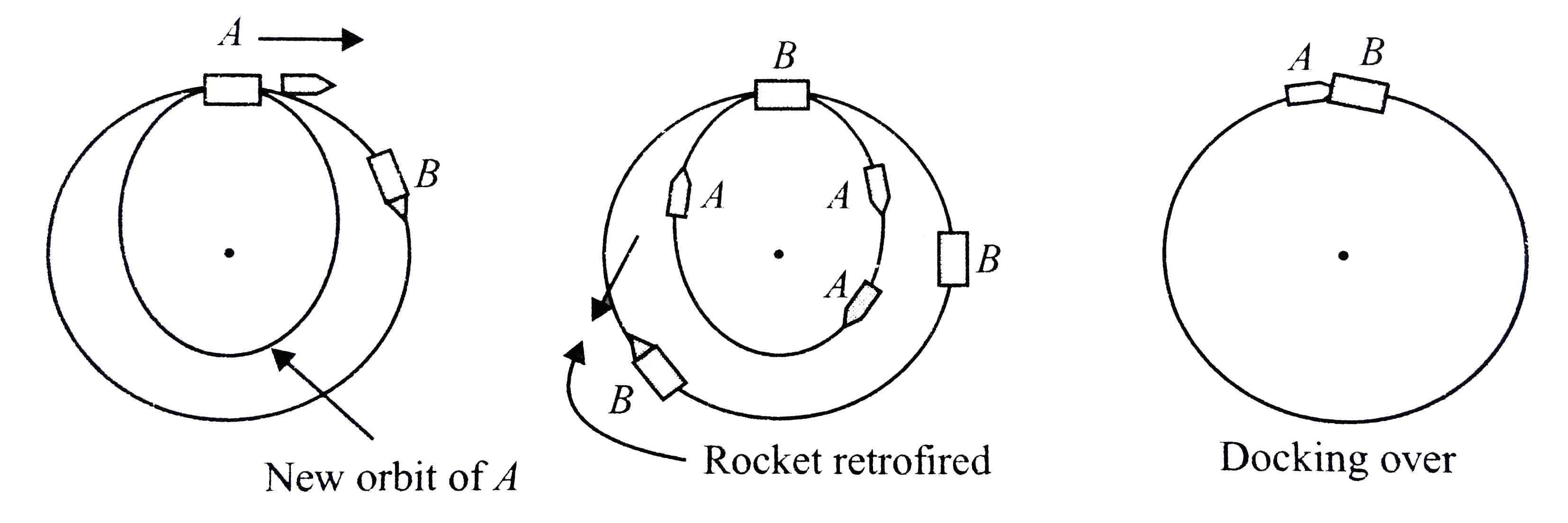
View SolutionAn unmanned satellite A and a spacecraft B are orbiting around the earth in the same circular orbit as shown.
 The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
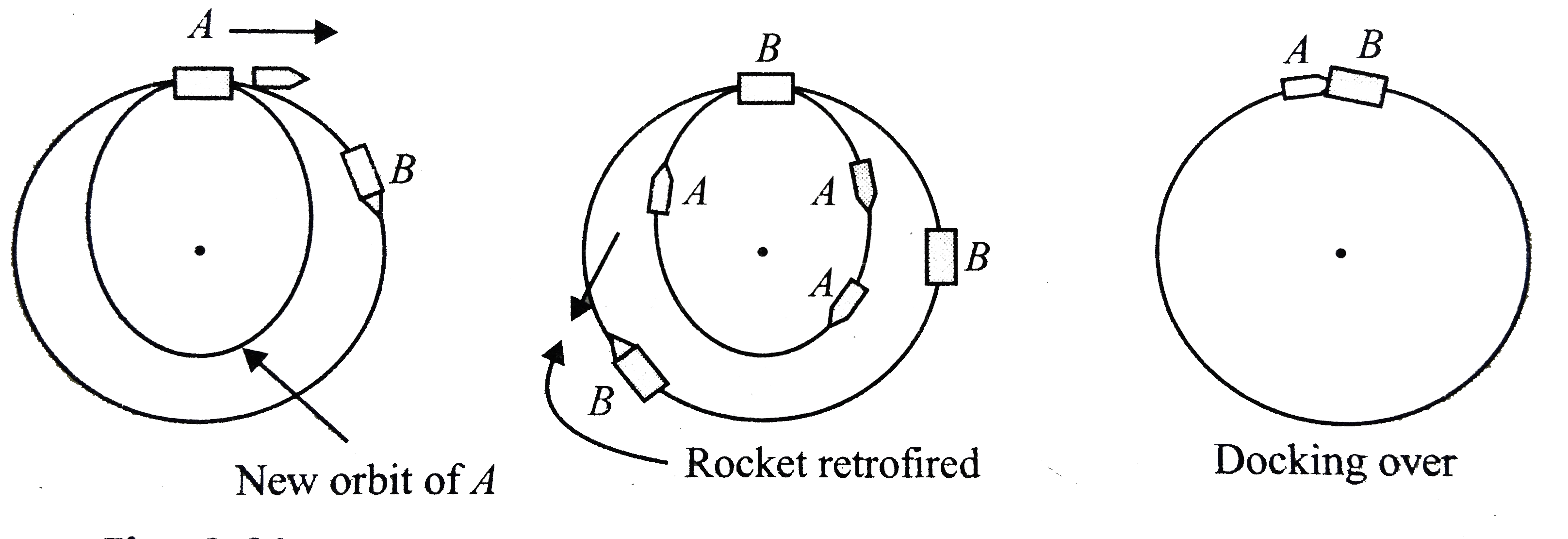
Take mass of the earth =5.98×1024kg
Radius of the earth =6400km
Orbital radius =9600km
Mass of satellite A=320kg
Mass of spacecraft =3200kg
Assume that initially spacecraft B leads satellite A by 100s, i.e., A arrives at any particle position after 100s of B’s arrival. Based on the above information answer the following questions
The initial total energy and time period of satellite are, respectively,
View SolutionAn unmanned satellite A and a spacecraft B are orbiting around the earth in the same circular orbit as shown.
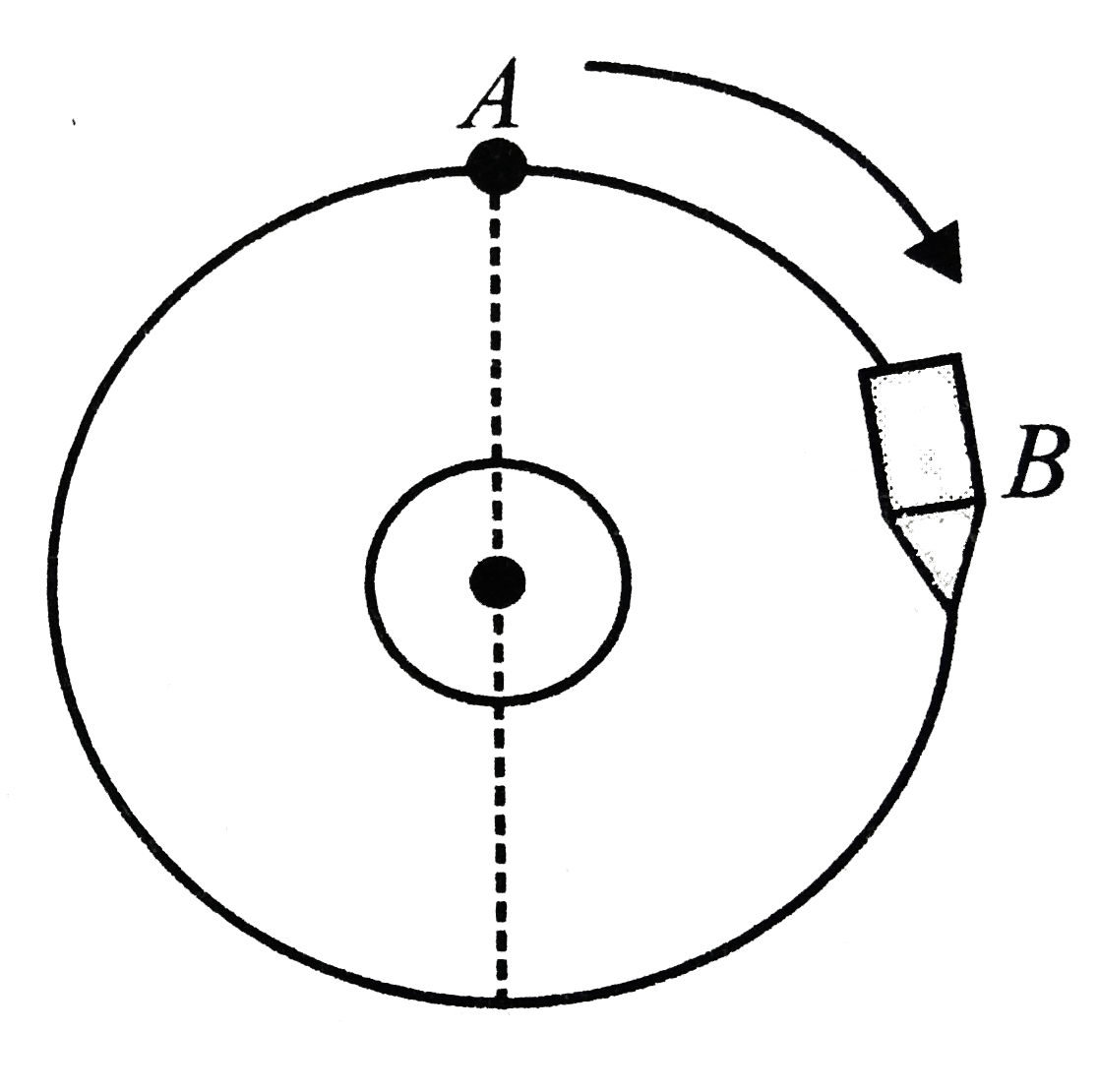 The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
Take mass of the earth =5.98×1024kg
Radius of the earth =6400km
Orbital radius =9600km
Mass of satellite A=320kg
Mass of spacecraft =3200kg
Assume that initially spacecraft B leads satellite A by 100s, i.e., A arrives at any particle position after 100s of B’s arrival. Based on the above information answer the following questions.
To dock A and B in the above-described situation, one can use the rocket system of either one, i.e., either of A or of B. To accomplish docking in the minimum possible time which is the best way?
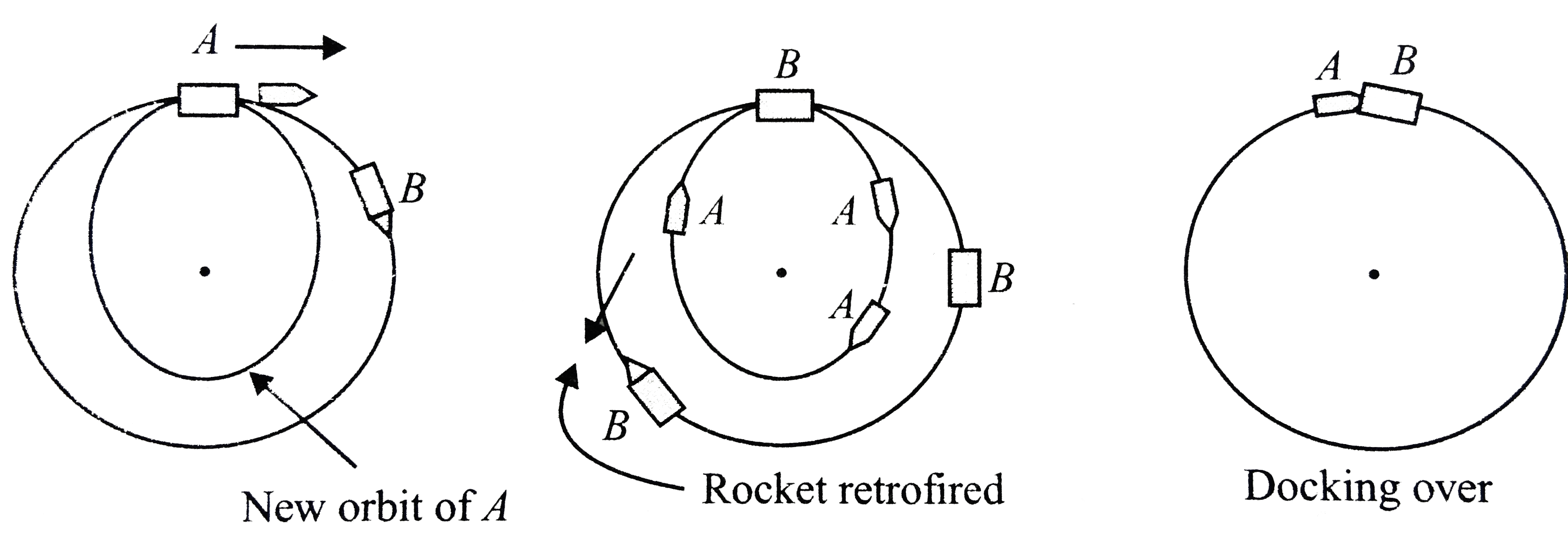
View SolutionAn unmanned satellite A and a spacecraft B are orbiting around the earth in the same circular orbit as shown.
 The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
Take mass of the earth =5.98×1024kg
Radius of the earth =6400km
Orbital radius =9600km
Mass of satellite A=320kg
Mass of spacecraft =3200kg
Assume that initially spacecraft B leads satellite A by 100s, i.e., A arrives at any particle position after 100s of B’s arrival. Based on the above information answer the following questions. After once returning to the original point, i.e., the place from where the rockets have been fired, in which direction and with what extent the rockets have to be fired from the satellite to again come back in the original orbit?
View SolutionA loop of rope is whirled at a high angular velocityω, so that it becomes a taut circle of radius r.
(a) Find the tension in the rope it the linear mass density of the rope is μ
(b) A kink develops in the whirling rope. Under what condition does the kink remain stationary relative to an observer on the ground?
View Solution
