A loop of rope is whirled at a high angular velocityω, so that it becomes a taut circle of radius r.
(a) Find the tension in the rope it the linear mass density of the rope is μ
(b) A kink develops in the whirling rope. Under what condition does the kink remain stationary relative to an observer on the ground?
The correct Answer is:(i)μr2ω2 , (ii)The loop rotates is opposite sense of the rotation of the kinck
Step by step video & image solution for A loop of rope is whirled at a high angular velocityomega, so that it becomes a taut circle of radius r. (a) Find the tension in the rope it the linear mass density of the rope is mu (b) A kink develops in the whirling rope. Under what condition does the kink remain stationary relative to an observer on the ground? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A loop of rope is whirled at a high angular velocityω, so that it becomes a taut circle of radiusR. A kink develops in the whirling rope.
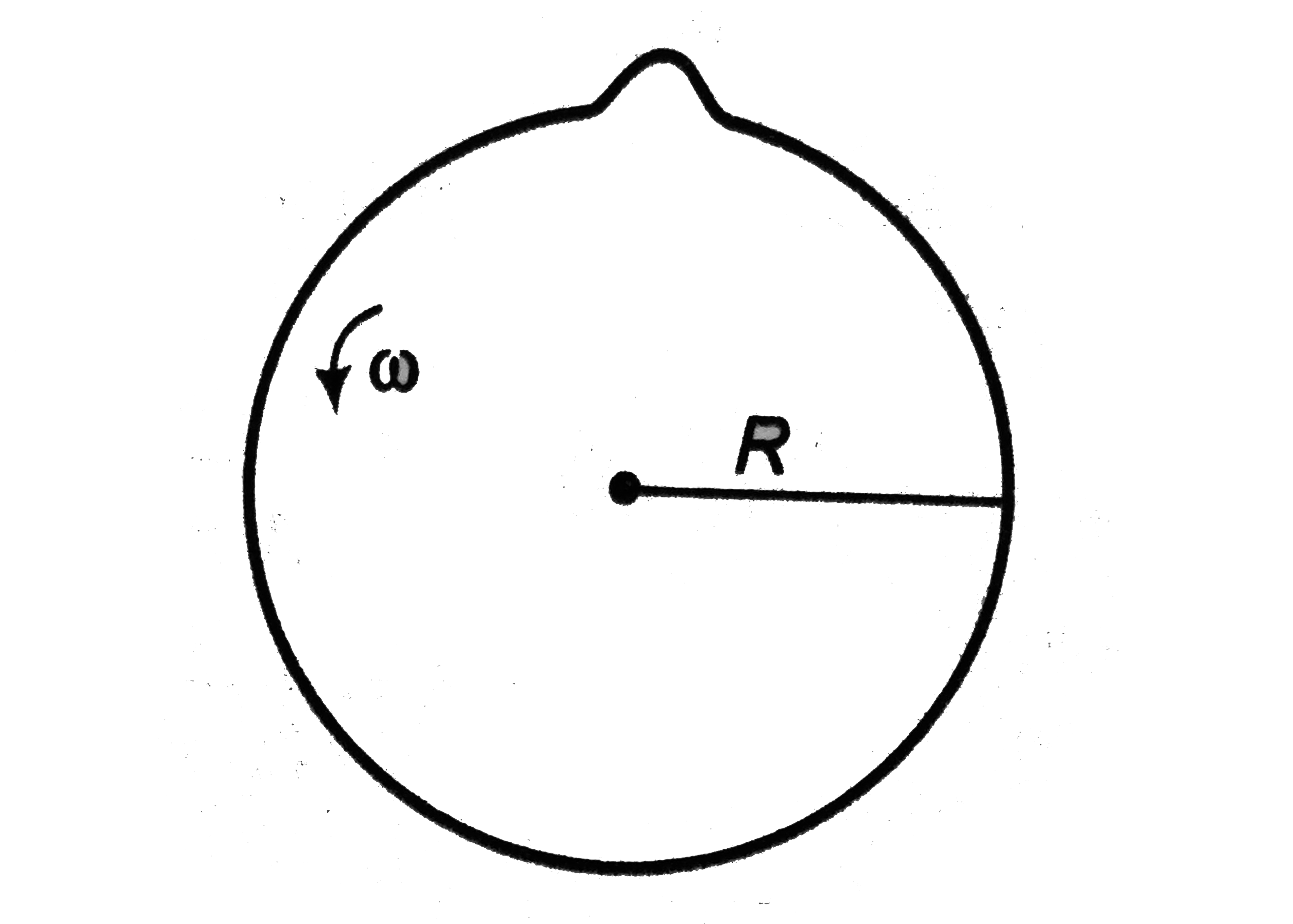
(a) Show that the speed of the kink in the rope is v=ωR.
(b) Under what conditions does the kink remains stationary relative to an observer on the ground?View SolutionA body of mass m is tied with rope and rotated along horizontal circle of radius r. If T is the tension in the rope and v is the velocity of body and an instant the force required for circular motion is
View SolutionA taut string having tension 100 N and linear mass density 0.25kg/m is used inside a cart to generate a wave pulse starting at the left end, as shown. What should be the velocity of the cart so that pulse remains stationary w.r.t. ground.
View SolutionA taut string having tension 100 N and linear mass density 0.25kg/m is used inside a cart to generate a wave pulse starting at the left end, as shown. What should be the velocity of the cart so that pulse remains stationary w.r.t. ground.
View SolutionA circular loop of rope of length L rotates with uniform angular velocity ω about an axis through its centre on a horizontal smooth platform. Velocity of pulse (with resppect to rope ) produce due to slight radiul displacement is given by ωL2π , if the motion of the pulse and rotation of the loop, both are in same direction then the velocity of the pulse w.r.t. to ground will be:
View SolutionA ring of mass m and radius r is rotated in uniform magnetic field B which is perpendicular to the plane of the loop with constant angular velocity ω0.Find the net ampere force on the ring and the tension developed in the ring if there is a current i in the ring.Current and rotation both are clockwise.
 View Solution
View SolutionA string has a linear mass density μ. The ends of the string are joined to form a closed loop and is given the shape of a circular ring of radius R. this ring is now rotated about its axis with an angular velocity ω
Q. The velocity of the transverse wave set up in the string, with respect to an observer at the centre ofView SolutionA hoop of mass m is projected on a floor with linear velocity v0 and reverse spin ω0. The coefficient of friction between the hoop and the ground is μ.
a. Under what condition will the hoop return back?
b. How far will it go?
c. How long will it continue to slip when its centre of mass becomes stationary?
d. What is the velocity of return?View SolutionA disc of radius R is rotating with an angular ω0 about a horizontal axis it is placed on a horizontal table . The coefficient of kinetic friction is μk
(a) what was the velocity of its centre of mass before being brought in contact with a the table ?
(B) what happens to the linear velocity of a point on its rim when placed in contact with the table ?
(c ) what happes to the linear speed of the centre of mass when disc is placed in contact with the table ?
(d) which force is responsible for the effects in (b) and (C ) ?
(e) wht condition should be sattisfied for rolling to begin ?
(f) Calculate the time taken for the rolling to begin .View SolutionA thick rope of length 2L and linear mass density 9μ is joined at B to a thin rope of length L and linear mass density 4μ. The systems horizontally stretched by the two vertical wall A and C. Assuming B to be a node, find the minimum number of loops in the thick rope.
 View Solution
View Solution

