A unifrom flexible chain of length 32 m rests on a fixed smooth sphere of radius R=2π m such that one end A of chain is on the top of the sphere while the other end B is hanging freely. Chain is helpd stationary by a horizontal thread PA as shown . Calculate the acceleration of chain when the horizontal string PA is burnt ( g = 10 m/s2)
The correct Answer is:(π+4)g3π
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We have a uniform flexible chain of length L=32 m resting on a smooth sphere of radius R=2π m. One end of the chain is at the top of the sphere (point A), and the other end (point B) is hanging freely. The chain is held stationary by a horizontal thread PA. We need to calculate the acceleration of the chain when the thread PA is burnt.
Step 2: Analyze the Forces Acting on the Chain
When the thread is burnt, the forces acting on the chain will be:
- The weight of the hanging portion of the chain, which we denote as F1.
- The tension in the chain due to the portion resting on the sphere, which we denote as F2.
Step 3: Calculate the Weight of the Hanging Portion
The length of the hanging portion of the chain is L2=3/22=34 m. The weight of this portion is given by:
F1=mass×g=(34⋅mL)⋅g=34⋅m32⋅10=34⋅2m3⋅10=5m2 N
Step 4: Calculate the Tension in the Chain Resting on the Sphere
The tension F2 can be calculated by integrating the forces acting on the chain resting on the sphere. The total force supporting the motion can be expressed as:
F2=∫π20mgcos(θ)dθ
where θ is the angle subtended by the chain at the center of the sphere. The limits of integration are from 0 to π2.
Calculating this integral gives:
F2=mg(sin(θ))π20=mg⋅1=mg
Step 5: Total Force Acting on the Chain
The total force acting on the chain when the thread is burnt is:
Fnet=F1+F2=5m2+mg
Step 6: Calculate the Net Acceleration
Using Newton's second law, the net acceleration a of the chain can be calculated as:
a=Fnetm=5m2+mgm=52+g
Substituting g=10m/s2:
a=52+10=2.5+10=12.5m/s2
Final Answer
The acceleration of the chain when the horizontal string PA is burnt is 12.5m/s2.
---
We have a uniform flexible chain of length L=32 m resting on a smooth sphere of radius R=2π m. One end of the chain is at the top of the sphere (point A), and the other end (point B) is hanging freely. The chain is held stationary by a horizontal thread PA. We need to calculate the acceleration of the chain when the thread PA is burnt.
When the thread is burnt, the forces acting on the chain will be:
- The weight of the hanging portion of the chain, which we denote as F1.
- The tension in the chain due to the portion resting on the sphere, which we denote as F2.
The length of the hanging portion of the chain is L2=3/22=34 m. The weight of this portion is given by:
F1=mass×g=(34⋅mL)⋅g=34⋅m32⋅10=34⋅2m3⋅10=5m2 N
The tension F2 can be calculated by integrating the forces acting on the chain resting on the sphere. The total force supporting the motion can be expressed as:
F2=∫π20mgcos(θ)dθ
where θ is the angle subtended by the chain at the center of the sphere. The limits of integration are from 0 to π2.
F2=mg(sin(θ))π20=mg⋅1=mg
The total force acting on the chain when the thread is burnt is:
Fnet=F1+F2=5m2+mg
Using Newton's second law, the net acceleration a of the chain can be calculated as:
a=Fnetm=5m2+mgm=52+g
Substituting g=10m/s2:
a=52+10=2.5+10=12.5m/s2
The acceleration of the chain when the horizontal string PA is burnt is 12.5m/s2.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Example
24 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE
69 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -I ) Subjective Type Questions
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
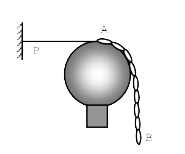
A chain of mass per unit length λ and length 1.5 m rests on a fixed smooth sphere of radius R=2πm such that A end of chain is at the top of sphere while the other end is hanging freely. Chain is held stationary by a horizontal thread PA. The tension in the thread is:
View SolutionA chain of length l and mass m lies on the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere.
View SolutionThe food chain ends with
View SolutionA chain of length l and mass m lies of the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.

View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain l<12πR.
View SolutionA uniform chain of mass m & length L is kept on a smooth horizontal table such that Lnportion of the chaing hangs from the table. The work dione required to slowly bringsthe chain completely on the table is
View SolutionA sphere of mass 20 g is whirled around in a horizontal circular path on the end of a string, the other end of which is stationary. If the tension in the string is 12.62 N, calculate the length of the string.
View SolutionA chain of mass m and length L is held at rest on smooth horizontal surface such that a part I of the chain is hanging vertically from the table. If the chain is let go, what is its speed as its end just leaves the horizontal surface?
View SolutionA uniform chain of length L lies on a smooth horizontal table with its length perpendicular to the edge of the table and a small portion of the chain is hanging over the edge. The chain starts sliding due to the weight of the hanging part
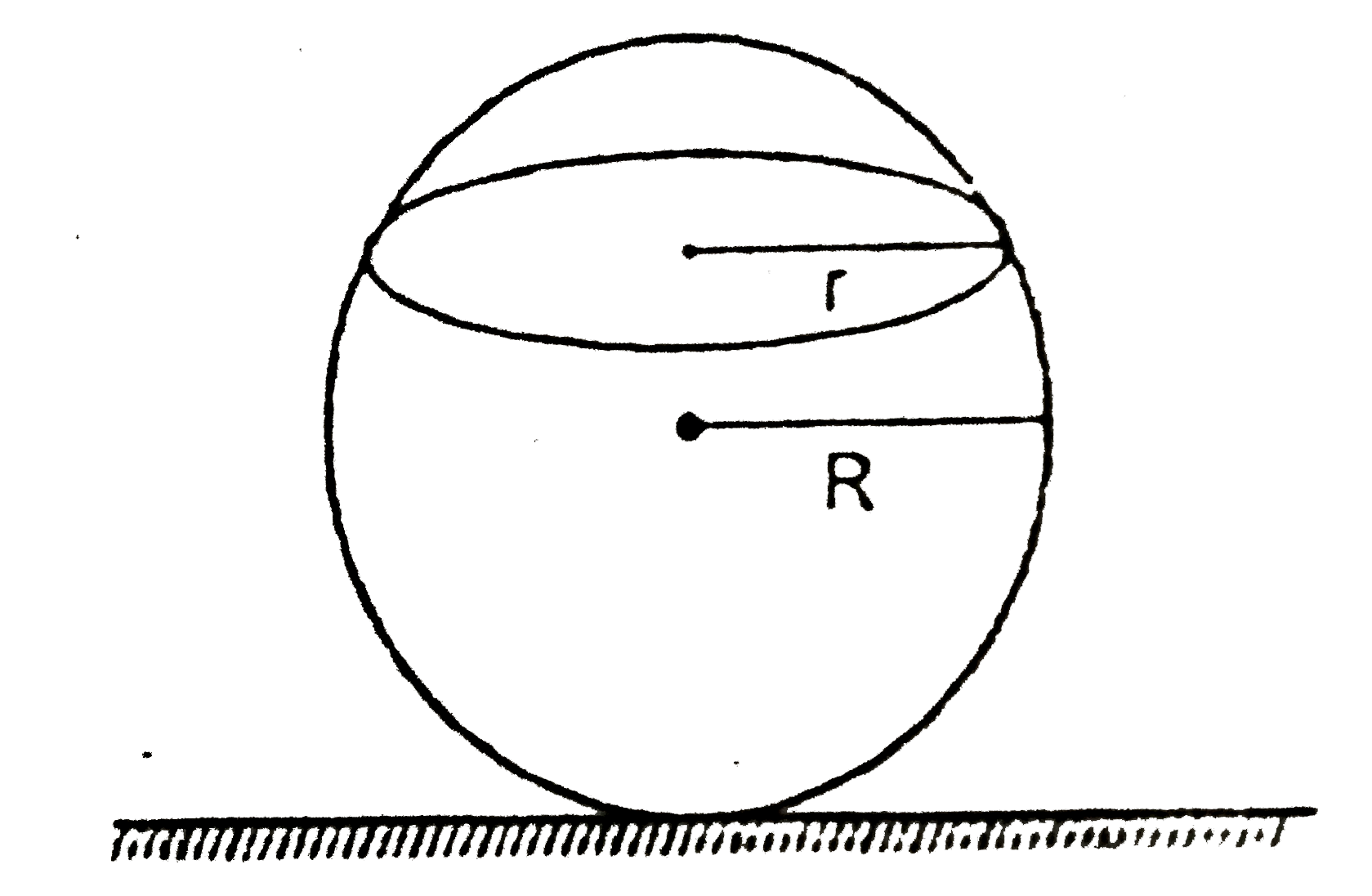
View SolutionA uniform circular chain of radius r and mass m rests over a sphere of radius R as shown in figure. Friction is absent everywhere and system is in equilibrium . Find the tension in the chain.
View Solution
