Given →F=→at where symbols have their usual meaning. The dimensions of a is .
The correct Answer is:[MLT−1]
To find the dimensions of →a given the equation →F=→at, we can follow these steps:
Step 1: Rearranging the equation
We start with the equation:
→F=→at
To find →a, we can rearrange the equation:
→a=→F⋅t
Step 2: Identifying the dimensions of force
Next, we need to identify the dimensions of force →F. The dimension of force is given by:
(→F)=(M)(L)(T−2)
This means that the dimensions of force are:
(→F)=MLT−2
Step 3: Identifying the dimensions of time
Now, we identify the dimensions of time t:
(t)=T
Step 4: Combining the dimensions
Now we can substitute the dimensions of →F and t back into our rearranged equation for →a:
(→a)=(→F)⋅(t)=(MLT−2)⋅(T)
Step 5: Simplifying the dimensions
Now we simplify the expression:
(→a)=MLT−2⋅T=MLT−1
Final Result
Thus, the dimensions of →a are:
(→a)=MLT−1
We start with the equation:
→F=→at
To find →a, we can rearrange the equation:
→a=→F⋅t
Next, we need to identify the dimensions of force →F. The dimension of force is given by:
(→F)=(M)(L)(T−2)
This means that the dimensions of force are:
(→F)=MLT−2
Now, we identify the dimensions of time t:
(t)=T
Now we can substitute the dimensions of →F and t back into our rearranged equation for →a:
(→a)=(→F)⋅(t)=(MLT−2)⋅(T)
Now we simplify the expression:
(→a)=MLT−2⋅T=MLT−1
Thus, the dimensions of →a are:
(→a)=MLT−1
Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (S-2)
7 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) Single Correct Type Questions.
34 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Solved Examples
7 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)
7 Videos
Similar Questions
The related equations are : Q=mc(T2−T1),l1=l0[1+α(T2−T1)] and PV−nRT,
where the symbols have their usual meanings. Find the dimension of
(A) specific heat capacity (C) (B) coefficient of linear expansion (α) and (C) the gas constant (R).
View SolutionDimensions of 1μ0∈0 , where symbols have their usual meaning are
View SolutionConsider a wave rpresented by y=acos2(ωt−kx) where symbols have their usual meanings. This wave has
View SolutionIn the relation V=π8Pr4nl , where the letters have their usual meanings , the dimensions of V are
View SolutionIf the electric field and magnetic field of an electromagnetic wave are related as B=Ec where the symbols have their usual meanings and the energy in a given volume of space due to the electric field part is U, then the energy due to the magnetic field part will be
View SolutionBohr magnetonis given by (symbols have their usual meanings)
View SolutionSymbols have their usual meanings. Match the Column-I with Column-II:
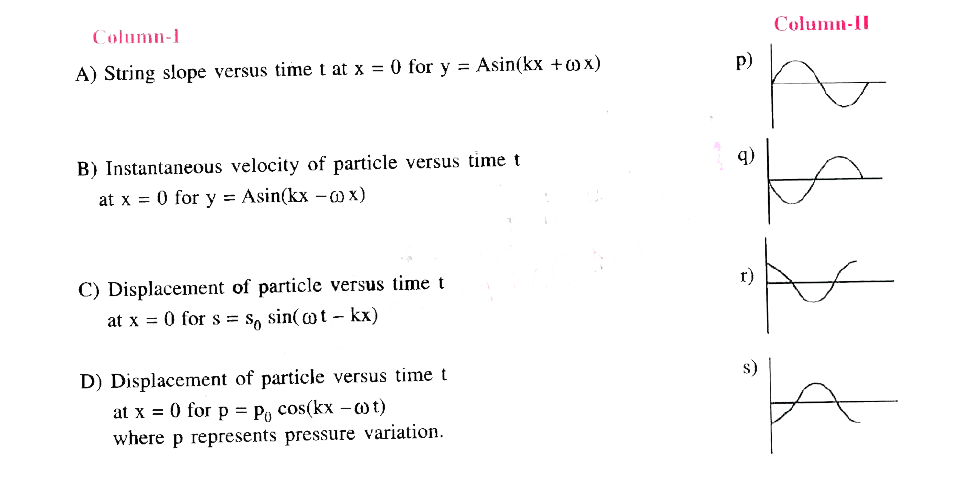
View SolutionSelect the incorrect relation. (Where symboles have their usual meanings):-
View SolutionIn YDSE, find the missing wavelength at y=d, where symbols have their usual meaning (takeD>>d).
View SolutionCalculate the dimensions of (a) ∫→E.d→l,(b)vBlanddΦ0dt. The symbols have their usual meanings.
View Solution
