A satellite is orbiting around a planet. Its orbital velocity (V0) is found to depend upon
(A) Radius of orbit (R)
(B) Mass of planet (M)
(C ) Universal gravitatin contant (G)
Using dimensional anlaysis find and expression relating orbital velocity (V0) to the above physical quantities.
The correct Answer is:v0=k√GMR
To find the expression relating the orbital velocity V0 of a satellite to the radius of orbit R, the mass of the planet M, and the universal gravitational constant G using dimensional analysis, we can follow these steps:
Step 1: Establish the relationship
We assume that the orbital velocity V0 depends on the radius of orbit R, the mass of the planet M, and the gravitational constant G. We can express this relationship as:
V0∝RaMbGc
where a, b, and c are the powers we need to determine.
Step 2: Write the equation
To remove the proportionality sign, we introduce a constant k:
V0=kRaMbGc
Step 3: Identify the dimensions
Next, we identify the dimensions of each quantity:
- The dimension of V0 (velocity) is (V0)=LT.
- The dimension of R (radius) is (R)=L.
- The dimension of M (mass) is (M)=M.
- The dimension of G (gravitational constant) can be derived from the formula for gravitational force F=Gm1m2R2. The dimensions of G are:
(G)=(F)(R2)(M2)=MLT−2L2M2=M−1L3T−2
Step 4: Write the dimensions in terms of a, b, and c
Now we can express the dimensions in terms of a, b, and c:
V0=kRaMbGc⟹LT=kLaMb(M−1L3T−2)c
This simplifies to:
LT=kLa+3cMb−cT−2c
Step 5: Equate the dimensions
Now we equate the dimensions on both sides:
1. For length L:
a+3c=1
2. For mass M:
b−c=0⟹b=c
3. For time T:
−2c=−1⟹c=12
Step 6: Solve for a and b
Using c=12 in the equations:
- From b=c:
b=12
- From a+3c=1:
a+3(12)=1⟹a+32=1⟹a=1−32=−12
Step 7: Substitute back into the equation
Now we have:
- a=−12
- b=12
- c=12
Substituting these values back into the equation gives:
V0=kR−12M12G12
This can be rewritten as:
V0=k√MGR
Final Expression
Thus, the expression relating the orbital velocity V0 to the radius of orbit R, mass of the planet M, and gravitational constant G is:
V0=k√MGR
We assume that the orbital velocity V0 depends on the radius of orbit R, the mass of the planet M, and the gravitational constant G. We can express this relationship as:
V0∝RaMbGc
where a, b, and c are the powers we need to determine.
To remove the proportionality sign, we introduce a constant k:
V0=kRaMbGc
Next, we identify the dimensions of each quantity:
- The dimension of V0 (velocity) is (V0)=LT.
- The dimension of R (radius) is (R)=L.
- The dimension of M (mass) is (M)=M.
- The dimension of G (gravitational constant) can be derived from the formula for gravitational force F=Gm1m2R2. The dimensions of G are:
(G)=(F)(R2)(M2)=MLT−2L2M2=M−1L3T−2
Now we can express the dimensions in terms of a, b, and c:
V0=kRaMbGc⟹LT=kLaMb(M−1L3T−2)c
This simplifies to:
LT=kLa+3cMb−cT−2c
Now we equate the dimensions on both sides:
1. For length L:
a+3c=1
2. For mass M:
b−c=0⟹b=c
3. For time T:
−2c=−1⟹c=12
Using c=12 in the equations:
- From b=c:
b=12
- From a+3c=1:
a+3(12)=1⟹a+32=1⟹a=1−32=−12
Now we have:
- a=−12
- b=12
- c=12
V0=kR−12M12G12
This can be rewritten as:
V0=k√MGR
Thus, the expression relating the orbital velocity V0 to the radius of orbit R, mass of the planet M, and gravitational constant G is:
V0=k√MGR
Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (S-2)
7 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) Single Correct Type Questions.
34 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Solved Examples
7 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)
7 Videos
Similar Questions
Knowledge Check
A satellite is moving around the earth with speed v in a circular orbit of radius r. IF the orbit radius is decreased by 1%, its speed will
Aincrease by 1%Bincrease by 0.5 %Cdecrease by 1%Ddecrease by 0.5 %
The period of revolution of a satellite depends upon the radius of the orbit, the mass of the planet and the gravitational constant. Prove that the square of the period varies as the cube of the radius.
View SolutionA satellite is revolving around a planet in a circular orbit. What will happen, if its speed is increased from υ0 to
(a) √1.5υ0 (b) 2υ0
View SolutionThe escape velocity of a body from the surface of the earth depends upon (i) the mass of the earth M, (ii) The radius of the eath R, and (iii) the gravitational constnat G. Show that v=k√GMR, using the dimensional analysis.
View SolutionTwo satellite of mass m and 9m are orbiting a planet in orbits of radius R. Their periods of revolution will be in the ratio of
View SolutionThe orbital velocity of an artifical satellite in a cirular orbit above the earth's surface at a distance equal to radiu of earth is v. For a satellite orbiting at an altitude half of earth's radius, orbital velocity is
View SolutionThe orbital speed of a satellite revolving around a planet in a circular orbit is v0 . If its speed is increased by 10 % ,then
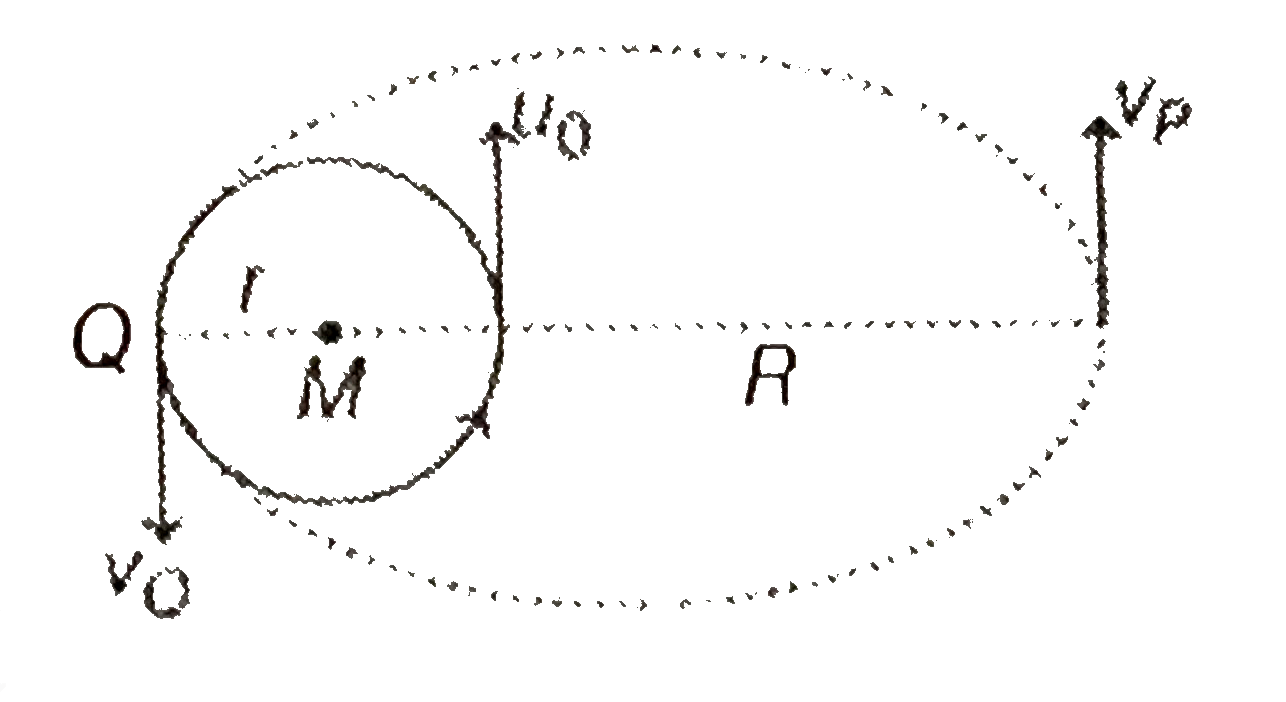
View SolutionA light satellite is initially rotating around a planet in a circular orbit of radius r. Its speed in this circular orbit was u0. It is put in an elliptical orbit by increasing its speed form u0 to vQ ( instantaneously). In the elliptical orbit, the satellite reaches the farthest point P, which is at a distance R from the planet. Satellite's speed at farthest point is vP. At point Q, the speed required by satellite to escape the planet's gravitational pull is vesc
View Solution
