A plumber steps down 1 m out of his truck and walks 50m east and then 25m South, and then takes an elevator to the basement of the building 9 m below steet level. If the east, the north and the upwards direction are represent by the positive x, y and z- axes, which one of the following represent displacement (meters ) of the plumber ?
50ˆi−25ˆj−9ˆk
50ˆi+25ˆj−9ˆk
50ˆi−25ˆj−10ˆk
50ˆi+25ˆj−10ˆk
The correct Answer is:C
To find the displacement of the plumber, we need to analyze his movements step by step and represent them in vector form.
1. Initial Step Down:
The plumber steps down 1 meter from his truck. Since the upward direction is positive along the z-axis, stepping down is represented as:
Displacement=−1^k
2. Walking East:
He walks 50 meters east. The east direction corresponds to the positive x-axis, so this displacement is:
Displacement=50^i
3. Walking South:
Next, he walks 25 meters south. The south direction corresponds to the negative y-axis, so this displacement is:
Displacement=−25^j
4. Taking the Elevator Down:
Finally, he takes an elevator down to the basement, which is 9 meters below street level. This downward movement is also along the z-axis and is represented as:
Displacement=−9^k
5. Total Displacement Calculation:
Now, we sum all these displacements to find the total displacement vector:
Total Displacement=(50^i)+(−25^j)+(−1^k)+(−9^k)
Simplifying this gives:
Total Displacement=50^i−25^j−10^k
Thus, the displacement of the plumber can be represented as:
Displacement=50^i−25^j−10^k meters
Final Answer:
The correct representation of the plumber's displacement is:
Displacement=50^i−25^j−10^k meters
The plumber steps down 1 meter from his truck. Since the upward direction is positive along the z-axis, stepping down is represented as:
Displacement=−1^k
He walks 50 meters east. The east direction corresponds to the positive x-axis, so this displacement is:
Displacement=50^i
Next, he walks 25 meters south. The south direction corresponds to the negative y-axis, so this displacement is:
Displacement=−25^j
Finally, he takes an elevator down to the basement, which is 9 meters below street level. This downward movement is also along the z-axis and is represented as:
Displacement=−9^k
Now, we sum all these displacements to find the total displacement vector:
Total Displacement=(50^i)+(−25^j)+(−1^k)+(−9^k)
Simplifying this gives:
Total Displacement=50^i−25^j−10^k
Displacement=50^i−25^j−10^k meters
The correct representation of the plumber's displacement is:
Displacement=50^i−25^j−10^k meters
Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-2) Multiple Correct Type Questions.
7 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-2) Comprehension Type Questions.
9 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) Matrix match type Questions.
2 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)
7 Videos
Similar Questions
The area under velocity-time graph gives the displacement whereas the slope of velocity-time graph at any point gives acceleration at that point. Slope is +ve if the line makes an acute angle in the anticlockwise direction with respect to the positive direction along which the independent variable increases. From the calculus, we also know that the slope of the tangent to a y vs. x graph is given by dydx If dydx is +ve then y increases with x, otherwise it decreases. Consider two persons namely Ram, and Rahim, who have gone to picnic at a nice place. Finding a beautiful place they rush towards it simultaneously. Let us take the time when they start simultaneously at t= 0 and at this instant the position of Ram and Rahim be x = 0 and x = + 48, respectively. Ram maintains a uniform velocity of +10 m/s throughout the journey whereas Rahim starts from rest and continuously accelerates with + 1m/s2
Q The position-time graph for the motions of Ram and Rahim is given by
View SolutionThe area under velocity-time graph gives the displacement whereas the slope of velocity-time graph at any point gives acceleration at that point. Slope is +ve if the line makes an acute angle in the anticlockwise direction with respect to the positive direction along which the independent variable increases. From the calculus, we also know that the slope of the tangent to a y vs. x graph is given by dydx If dydx is +ve then y increases with x, otherwise it decreases. Consider two persons namely Ram, and Rahim, who have gone to picnic at a nice place. Finding a beautiful place they rush towards it simultaneously. Let us take the time when they start simultaneously at t= 0 and at this instant the position of Ram and Rahim be x = 0 and x = + 48, respectively. Ram maintains a uniform velocity of +10 m/s throughout the journey whereas Rahim starts from rest and continuously accelerates with + 1m/s2
Q The velocity-time graph as well as the acceleration-time graph of Ram and Rahim are respectively,

View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

The slope of the line segments plotted in figure 2 is a figure constant. Which one of the following physical quantities does this slope represent?
View SolutionStationary wave is setup in a uniform string clamped at both the ends. Length of the string is 0.3 m.Snapshot of the string is taken the two instants one at t=0 sec and another at t=0.2 sec. These is two snapshots are shown below.
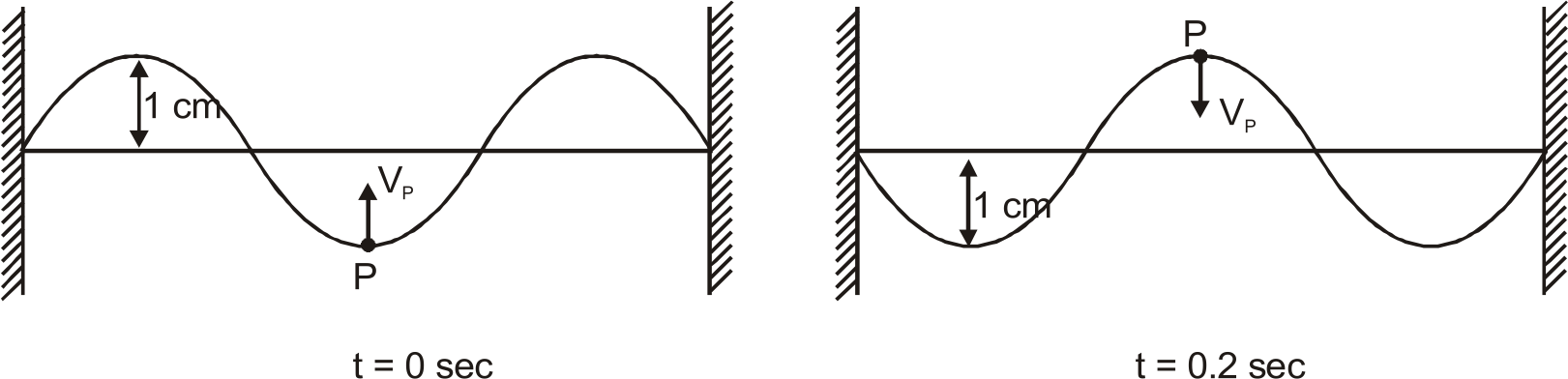
Velocity of point P (which is also the mid point of the string ) is in upward direction (take upward direction to be positive ) at t=0 sec.At the instant snapshots are taken particles are at half of their respective maximum displacement from mean position.During this time interval particles have crossed their mean position only once.Answer the following 3 questions for the qiven situation.
Velocity of travelling wave in the string is :
View SolutionStationary wave is setup in a uniform string clamped at both the ends. Length of the string is 0.3 m.Snapshot of the string is taken the two instants one at t=0 sec and another at t=0.2 sec. These is two snapshots are shown below.
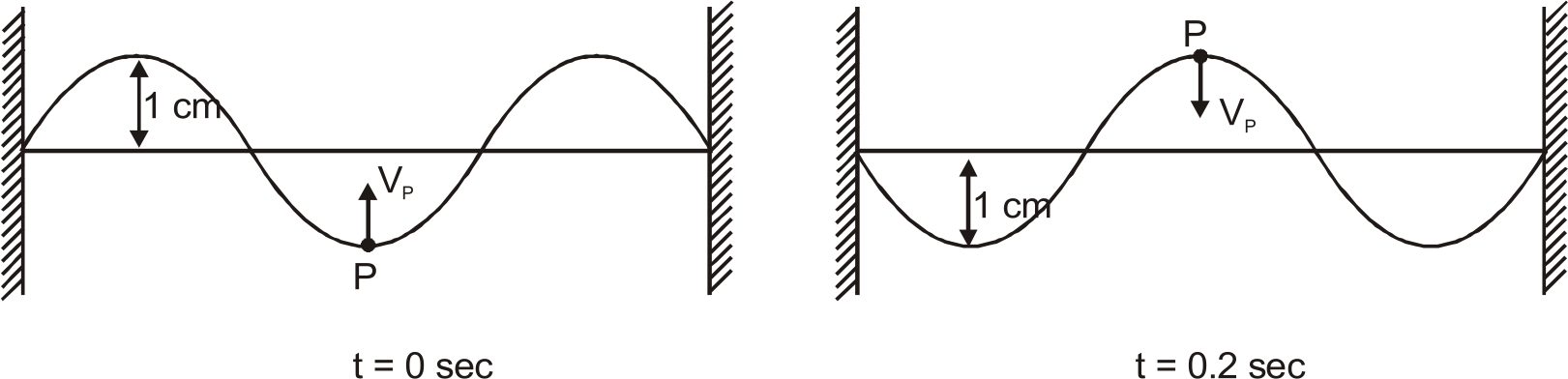
Velocity of point P (which is also the mid point of the string ) is in upward direction (take upward direction to be positive ) at t=0 sec.At the instant snapshots are taken particles are at half of their respective maximum displacement from mean position.During this time interval particles have crossed their mean position only once.Answer the following 3 questions for the qiven situation.
Velocity time graph of particle at mid point of the string (i.e. particle P)
View SolutionA man has to go 50 m due north, 40 m due east and 20 m due south to reach a field, What distance he has to walk to reach the field? b.What is his displacement from his house to the field?
View SolutionA plank fitted with a gun is moving on a horizontal surface with speed of 4m/s along the positive x-axis. The z-axis is in vertically upward direction. The mass of the plank including the mass of the gun is 50 kg. When the plank reaches the origin, a shell of mass 10 kg is fired at an angle of 60∘ with the positive x-axis with a speed of v=20m/s with respect to the gun in x-z plane. Find the position vector of the shell at t=2 s after firing it. Take g=9.8m/s2.
View SolutionAn elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
3. Displacement of ball with respect to ground during its night would be
View SolutionA 100Hz sinusoidal wave is travelling in the posotive x-direction along a string with a linear mass density of 3.5×10−3kg/m and a tension of 35N. At time t=0, the point x=0 , has maximum displacement in the positive y-direction. Next when this point has zero displacement, the slope of the string is π/20. Which of the following expression represent (s) the displacement of string as a function of x(in metre) and t (in second)
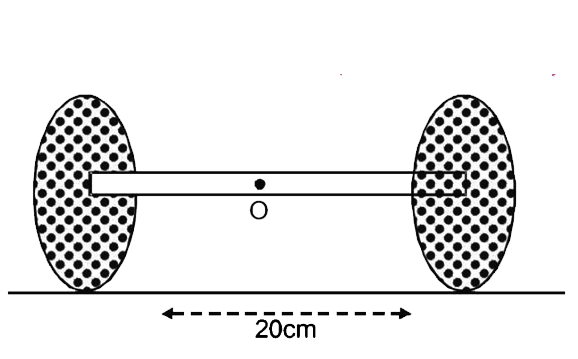
View SolutionTwo thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of 9m/s2 Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors ˆi,ˆjandˆk in the x,y, and z directions.
View Solution
