A body moves in anticlockwise direction on a circular path in the x-y plane. The radius of the circular path is 5m and its centre is at the origin. In a certain interval of time, displacement of the body is obesrved to be 6m in the positive y-direction. Which of the following is true ?
Its initial position vector is 5ˆi m
Its initial position vector is (−3ˆi+4ˆj) m.
Its final position vector is (4ˆi+3ˆj)m.
Its final position vector is 6ˆj m.
The correct Answer is:C
To solve the problem, we need to analyze the motion of the body moving in an anticlockwise direction on a circular path with a radius of 5 m. The displacement of the body is given as 6 m in the positive y-direction.
1. Understanding the Circular Motion:
- The body moves in a circular path with a radius of 5 m, centered at the origin (0,0) in the x-y plane.
- The position of the body can be represented using the angle θ made with the x-axis.
2. Position Vector Representation:
- The position vector →r of the body at any angle θ can be expressed as:
→r=5cos(θ)^i+5sin(θ)^j
3. Displacement Vector:
- The displacement is given as 6 m in the positive y-direction, which can be represented as:
Δ→r=0^i+6^j
4. Initial and Final Position Vectors:
- Let the initial position vector be →rinitial=5cos(θinitial)^i+5sin(θinitial)^j
- Let the final position vector be →rfinal=5cos(θfinal)^i+5sin(θfinal)^j
5. Calculating the Change in Position Vector:
- The change in position vector (displacement) is given by:
Δ→r=→rfinal−→rinitial
- This can be expressed as:
Δ→r=(5cos(θfinal)−5cos(θinitial))^i+(5sin(θfinal)−5sin(θinitial))^j
6. Setting Up the Equations:
- From the displacement vector, we know:
0^i+6^j=(5cos(θfinal)−5cos(θinitial))^i+(5sin(θfinal)−5sin(θinitial))^j
- This gives us two equations:
1. 5cos(θfinal)−5cos(θinitial)=0
2. 5sin(θfinal)−5sin(θinitial)=6
7. Solving the Equations:
- From the first equation, we can simplify:
cos(θfinal)=cos(θinitial)
- From the second equation:
sin(θfinal)−sin(θinitial)=65
8. Using the Sine and Cosine Values:
- The maximum value of sin is 1, which means the change in sine must be valid within the range of the sine function. This indicates that the angles must be such that:
sin(θfinal)=sin(θinitial)+65
- This is impossible since the sine function cannot exceed 1. Therefore, the values of θinitial and θfinal must be such that they yield a valid sine value.
9. Conclusion:
- The only valid conclusion is that the body must have moved in a way that maintains the circular path while achieving the given displacement in the y-direction. The angles must be such that the cosine values are equal, and the sine values differ by a maximum of 1.
- The body moves in a circular path with a radius of 5 m, centered at the origin (0,0) in the x-y plane.
- The position of the body can be represented using the angle θ made with the x-axis.
- The position vector →r of the body at any angle θ can be expressed as:
→r=5cos(θ)^i+5sin(θ)^j
- The displacement is given as 6 m in the positive y-direction, which can be represented as:
Δ→r=0^i+6^j
- Let the initial position vector be →rinitial=5cos(θinitial)^i+5sin(θinitial)^j
- Let the final position vector be →rfinal=5cos(θfinal)^i+5sin(θfinal)^j
- The change in position vector (displacement) is given by:
Δ→r=→rfinal−→rinitial
- This can be expressed as:
Δ→r=(5cos(θfinal)−5cos(θinitial))^i+(5sin(θfinal)−5sin(θinitial))^j
- From the displacement vector, we know:
0^i+6^j=(5cos(θfinal)−5cos(θinitial))^i+(5sin(θfinal)−5sin(θinitial))^j
- This gives us two equations:
1. 5cos(θfinal)−5cos(θinitial)=0
2. 5sin(θfinal)−5sin(θinitial)=6
- From the first equation, we can simplify:
cos(θfinal)=cos(θinitial)
- From the second equation:
sin(θfinal)−sin(θinitial)=65
- The maximum value of sin is 1, which means the change in sine must be valid within the range of the sine function. This indicates that the angles must be such that:
sin(θfinal)=sin(θinitial)+65
- This is impossible since the sine function cannot exceed 1. Therefore, the values of θinitial and θfinal must be such that they yield a valid sine value.
- The only valid conclusion is that the body must have moved in a way that maintains the circular path while achieving the given displacement in the y-direction. The angles must be such that the cosine values are equal, and the sine values differ by a maximum of 1.
Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-2) Multiple Correct Type Questions.
7 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-2) Comprehension Type Questions.
9 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) Matrix match type Questions.
2 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)
7 Videos
Similar Questions
A person runs along a circular path of radius 5 m. If he completes half of the circle find the magnitude of the displacement vector, How far the person ran ?
View SolutionA circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
View SolutionA point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of 'P ' is such that it sweeps out a length s=t3+5 where s is in meters and t is in seconds. The radius of the path is 20 m. The acceleration of ' P ' when t = 2 s is nearly:

View SolutionA particle is moving along a circular path in xy-plane. When it crosses x-axis, it has an acceleration along the path of 1.5m/s2, and is moving with a speed of 10m/s in -ve y - direction. The total acceleration is

View SolutionA particle of mass 'm' moves along the quarter section of the circular path whose centre is at the origin . The radius of the circular path is 'a'. A force →F=yˆi−xˆj newton acts on the particle, where x,y denote the coordinates of position of the particle. Calculate the work done by this force in taking, the particle from point, A(a,0) to point B(0,a) along the circular path.
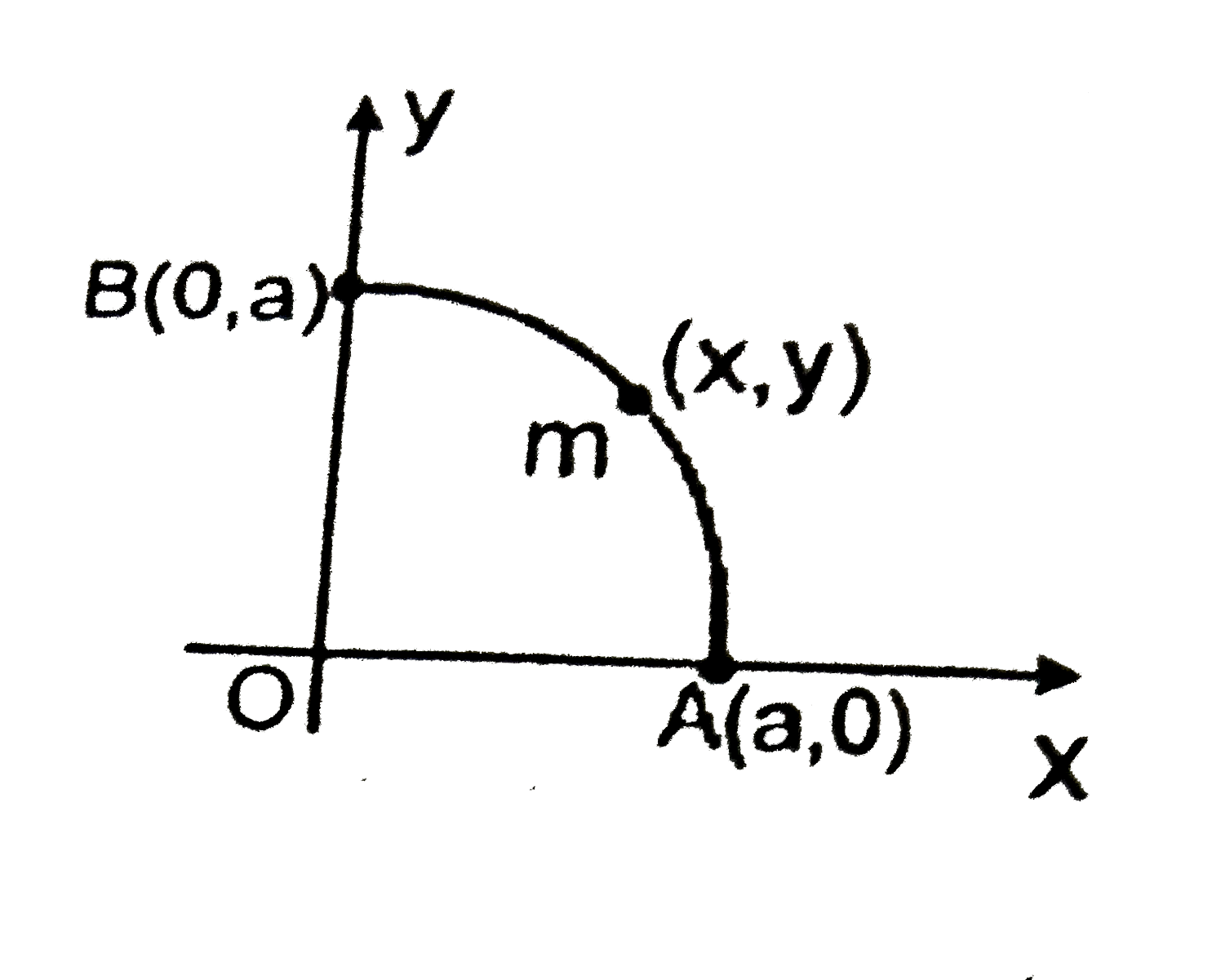
View SolutionA person runs along a circular path of radius 5 m. Find the magnitude of the displacement if he runs all the way around the circle ?
View SolutionA particle of mass m is rotating in a plane in circular path of radius r. Its angular momentum is L. The centripetal force acting on the particle is
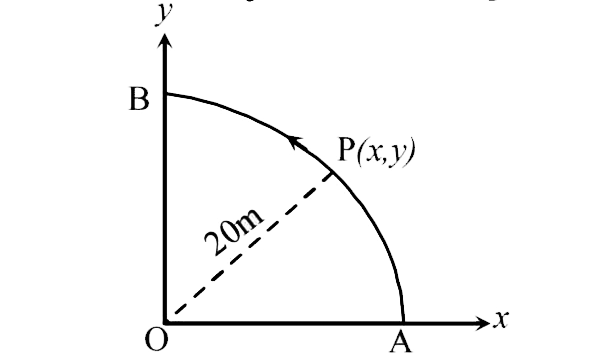
View SolutionA point p moves in counter - clockwise direction on a circular path as shown in the figure . The movement of 'p' is such that it sweeps out in the figure . The movement of 'p' is such that it sweeps out a length s=t3+5 , where s is in metres and t is in seconds . The radius of the path is 20m . The acceleration of 'P' when t=2s is nearly .
View SolutionAn object moves at constant speed along a cicular path in a horizontal xy plane. With the centre as origin.when the object is at x= -2m , it s velocity is −4ˆjm/s , its acceleration when it is at y= 2 m/s
View SolutionA car is moving with speed of 2ms−1 on a circular path of radius 1 m and its speed is increasing at the rate of 3ms(−1) The net acceleration of the car at this moment in m/s2 is
View Solution
