A man rows a boat with a speed of 18 km/hr in northwest direction. The shoeline makes an angle of 15∘ south of west. Obtain the component of the velocity of the boat along the shoreline:
9 km/hr
18√32km/hr
18cos(15∘)km/hr
18cos(75∘)km/hr
The correct Answer is:A
To solve the problem, we need to find the component of the velocity of the boat along the shoreline. Here’s a step-by-step solution:
Step 1: Understand the Directions
The boat is moving in the northwest direction, which is at an angle of 45 degrees from both the north and west axes. The shoreline is at an angle of 15 degrees south of west.
Step 2: Determine the Angle Between the Boat's Velocity and the Shoreline
Since the shoreline is 15 degrees south of west, we can find the angle between the direction of the boat (northwest) and the shoreline.
- The northwest direction is 45 degrees from the west.
- The shoreline is 15 degrees south of west, which is equivalent to 360 - 15 = 345 degrees from the north.
Thus, the angle between the boat's direction and the shoreline is:
Angle=45∘+15∘=60∘
Step 3: Calculate the Component of Velocity Along the Shoreline
The velocity of the boat is given as 18 km/hr. To find the component of this velocity along the shoreline, we can use the cosine of the angle we found:
Component of velocity along the shoreline=V⋅cos(θ)
Where:
- V=18 km/hr (velocity of the boat)
- θ=60∘ (angle between the boat's direction and the shoreline)
Now substituting the values:
Component=18⋅cos(60∘)
Step 4: Calculate cos(60∘)
We know that:
cos(60∘)=12
Step 5: Final Calculation
Now substituting back into the equation:
Component=18⋅12=9 km/hr
Conclusion
The component of the velocity of the boat along the shoreline is 9 km/hr.
---
The boat is moving in the northwest direction, which is at an angle of 45 degrees from both the north and west axes. The shoreline is at an angle of 15 degrees south of west.
Since the shoreline is 15 degrees south of west, we can find the angle between the direction of the boat (northwest) and the shoreline.
- The northwest direction is 45 degrees from the west.
- The shoreline is 15 degrees south of west, which is equivalent to 360 - 15 = 345 degrees from the north.
Angle=45∘+15∘=60∘
The velocity of the boat is given as 18 km/hr. To find the component of this velocity along the shoreline, we can use the cosine of the angle we found:
Component of velocity along the shoreline=V⋅cos(θ)
Where:
- V=18 km/hr (velocity of the boat)
- θ=60∘ (angle between the boat's direction and the shoreline)
Component=18⋅cos(60∘)
We know that:
cos(60∘)=12
Now substituting back into the equation:
Component=18⋅12=9 km/hr
The component of the velocity of the boat along the shoreline is 9 km/hr.
Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-2) Multiple Correct Type Questions.
7 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-2) Comprehension Type Questions.
9 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) Matrix match type Questions.
2 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)
7 Videos
Similar Questions
A man rows a boat with a speed of 18Kmh−1 in the north-west direction (figure). The shoreline makes an angle of 15∘ south of west. Obtain the components of the velocity of the boat along the shoreline and perpendicular to the shoreline.

View SolutionA boat which has a speed of 5km/hr in steel water crosses a river of width 1km along the shortest possible path in 15minutes. The velocity of the river water in km/hr is
View SolutionA boat which has a speed of 5km/hr in steel water crosses a river of width 1km along the shortest possible path in 15minutes. The velocity of the river water in km/hr is
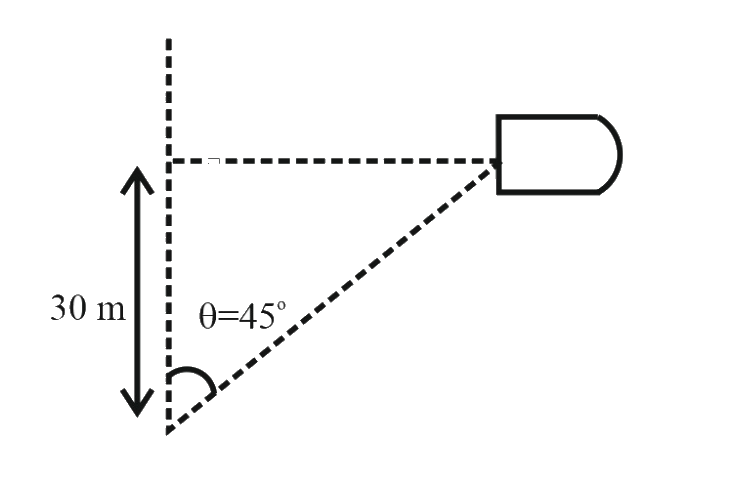
View SolutionA boat is travelling with a speed of 27 km h−1 due east. An observer is situated at 30 m south of the line of travel. The angular velocity of the boat relative to be the observer in the position shown will be
View SolutionThe raindrops are hitting the back of a man walking at a speed of 5km/hr. If he now starts running in the same direction with a constant acceleration, the magnitude of the velocity of the rain with respect to him will
View SolutionThe raindrops are hitting the back of a man walking at a speed of 5km/hr. If he now starts running in the same direction with a constant acceleration, the magnitude of the velocity of the rain with respect to him will
View SolutionA boat man can row with a speed of 10 km/hr. in still water. The river flow steadily at 5 km/hr. and the width of the river is 2 km. if the boat man cross the river with reference to minimum distance of approach then time elapsed in rowing the boat will be:-
View SolutionA boat which has a speed of 6km/h in still water crosses a river of width 1 km along the shortest possible path in 20 min. the velocity of the river water in km/h is
View SolutionA particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

View SolutionA man is on ship which is moving in east direction with speed 60km/hr. Waves of ocean is taking ship towards west with speed 20km/hr. Man start running on ship with flag in his hand in north direction with speed 30km/hr and wind is blowing with 50km/hr,37∘ towards south of west then find the direction of flutter the flag as seen by man on ground.
View Solution
