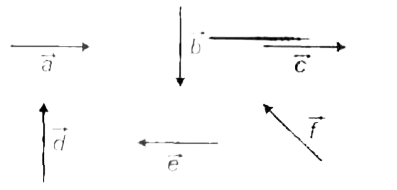
Six vector $\to a$ through $\to f$ have the magnitudes and direction indicated in the figure. Which of the following statements is true?

b+c=f

d+c=f

b+e=f

d+e=f

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Answer

Step by step video, text & image solution for Six vector vec(a) through vec(f) have the magnitudes and direction indicated in the figure. Which of the following statements is true? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS BASIC MATHS

Topper's Solved these Questions

BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Comprehension 1
5videos
BASIC MATHS
BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Comprehension 2
3videos
BASIC MATHS
BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Exersice-03
7videos
BASIC MATHS
BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS
40videos
AIIMS 2019
BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6videos
CIRCULAR MOTION

Knowledge Check

Question 1 - Select One
The magnitude of the x-component of vector $\to A$ is 3 and the magnitude of vector $\to A$ is 5. What is the magnitude of the y-component of vector $\to A$ ?
A3
B4
C5
D8

A particle performs SHM along a straight line and its position is $\to R$ , acceleration is $\to a$ , velocity is $\to v$ is and force on particle is $\to f$ . Then which of the following statement are true?
(i) $\to v . \to a$ is always + ve
(ii) $\to v . \to R$ may be -ve
(iii) $\to f . \to R$ is always -ve
(iv) $\to v$ is parallel to $\to f$ sometimes
View Solution
Statement 1: If $∣ ∣ \to a + \to b ∣ ∣ = ∣ ∣ \to a - \to b ∣ ∣$ , then $\to a$ and $\to b$ are perpendicular to each other. Statement 2: If the diagonal of a parallelogram are equal magnitude, then the parallelogram is a rectangle. Which of the following Statements is/are correct ?
View Solution
Three coplanar vectrors $\to A, \to B$ and $\to C$ have magnitudes $4, 3$ and $2$ respectively. If the angle any two vector is $120^{\circ}$ then which of the following vector may be equal to $\frac{3 \to A}{4} + \frac{\to B}{3} + \frac{\to C}{2}$

View Solution
$\to A$ is a vector with magnitude A, then the unit vector $ˆ A$ in the direction $\to A$ is
View Solution
If $\to r$ is a vector of magnitude 21 and has direction ratios $2, - 3 a n d 6,$ then find $\to r .$
View Solution
The resultant and dot product of two vectors $\to a and \to b$ is equal to the magnitude of $\to a$ . Show that when the vector $\to a$ is doubled , the new resultant is perpendicular to $\to b$ .
View Solution
If $\to a, \to b, \to c$ are non coplanar non-zero vectors such that $\to b \times \to c = \to a, \to a \times \to b = \to c$ and $\to c \times \to a = \to b$ , then which of the following is not true
View Solution

ALLEN-BASIC MATHS-ASSERTION-REASON

If |vecA xx vecB| = vecA.vecB then the angle between vecA and vecB is ...
01:20
A unit radial vector vecr makes agles of a=30^(@) relative to the x-ax...
01:32
If hati,hatj and hatk represent unit vectors along the x,y and z-axes ...
01:29
Find the torque (vectau=vecrxxvecF) of a force vecF=-3hati+hatj+3hatk ...
01:35
Six vector vec(a) through vec(f) have the magnitudes and direction ind...
03:55
If vectors vecA and vecB are such that |vecA+vecB|= |vecA|= |vecB| the...
03:43
The equation of a curve is given as y=x^(2)+2-3x. The curve intersec...
01:56
The sum of the series 1+(1)/(4)+(1)/(16)+(1)/(64)+....oo is
01:10
As theta increases from 0^(@) to 90^(@), the value of cos theta is
01:21
The coordinates of a particle moving in XY-plane very with time as x=4...
01:11
The slope of graph as shown in figure at points 1,2 and 3 is m(1), m(2...
01:34

Home
Ask Doubt
Profile

Six vector →a through →f have the magnitudes and direction indicated in the figure. Which of the following statements is true?

The correct Answer is:D

Topper's Solved these Questions

Similar Questions

Knowledge Check

The magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?

ALLEN-BASIC MATHS-ASSERTION-REASON

Six vector $\to a$ through $\to f$ have the magnitudes and direction indicated in the figure. Which of the following statements is true?

The magnitude of the x-component of vector $\to A$ is 3 and the magnitude of vector $\to A$ is 5. What is the magnitude of the y-component of vector $\to A$ ?