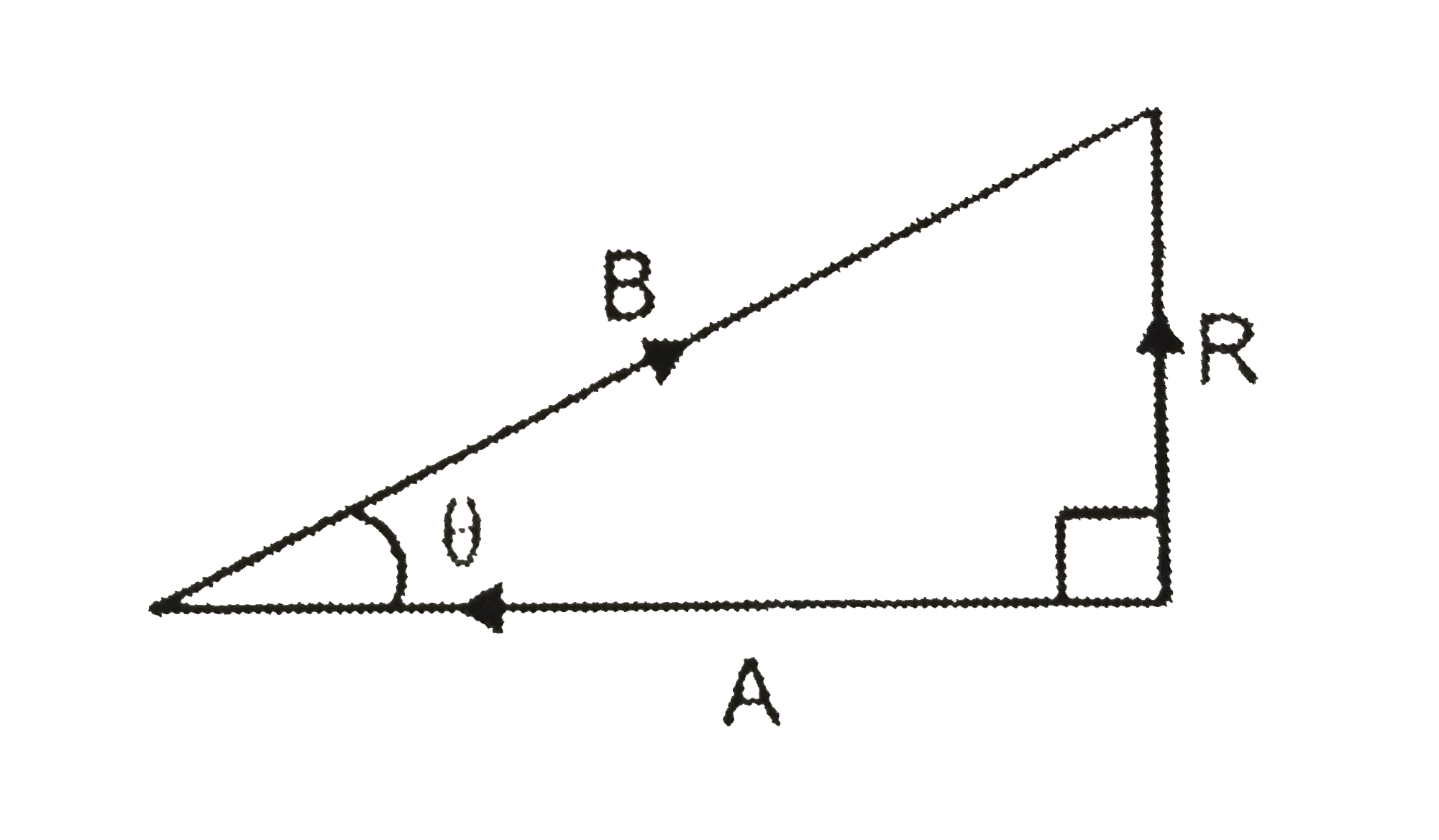
In vector diagram shown in figure where $(\to R)$ is the resultant of vectors $(\to A)$ and $(\to B)$ . If $R = \frac{B}{\sqrt{2}}$ , the value of angle $θ$ is :

A

68.57 s

B

0.6857 s

C

6.857 s

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

By solving above equation $T_{1} = 6.857 T$
$= 6.857 s$

|

Updated on:21/07/2023

Class 12 PHYSICS BASIC MATHS

Topper's Solved these Questions

BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - DATA SUFFICIENCY QUESTIONS
3videos
BASIC MATHS
BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Exercise-04 [A]
27videos
BASIC MATHS
BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Comprehension 3
3videos
BASIC MATHS
BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS
40videos
AIIMS 2019
BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6videos
CIRCULAR MOTION

Similar Questions

Knowledge Check

Question 1 - Select One
If $θ$ is the angle between any two vectors $\to a and \to b$ , then $∣ ∣ \to a . \to b ∣ ∣ = ∣ ∣ \to a \times \to b ∣ ∣$ when $θ$ is equal to
A0
B $\frac{π}{4}$
C $\frac{π}{2}$
D $π$
Question 2 - Select One
The angle between the two vectors $\to a + \to b$ and $\to a - \to b$ is
ABetween $0^{\circ}$ and $180^{\circ}$
B $90^{\circ}$ only
C $0^{\circ}$ only
D $180^{\circ}$ only

ALLEN-BASIC MATHS-Comprehension 4

Home
Ask Doubt
Profile