In vector diagram shown in figure where $(\to R)$ is the resultant of vectors $(\to A) and (\to B)$ .

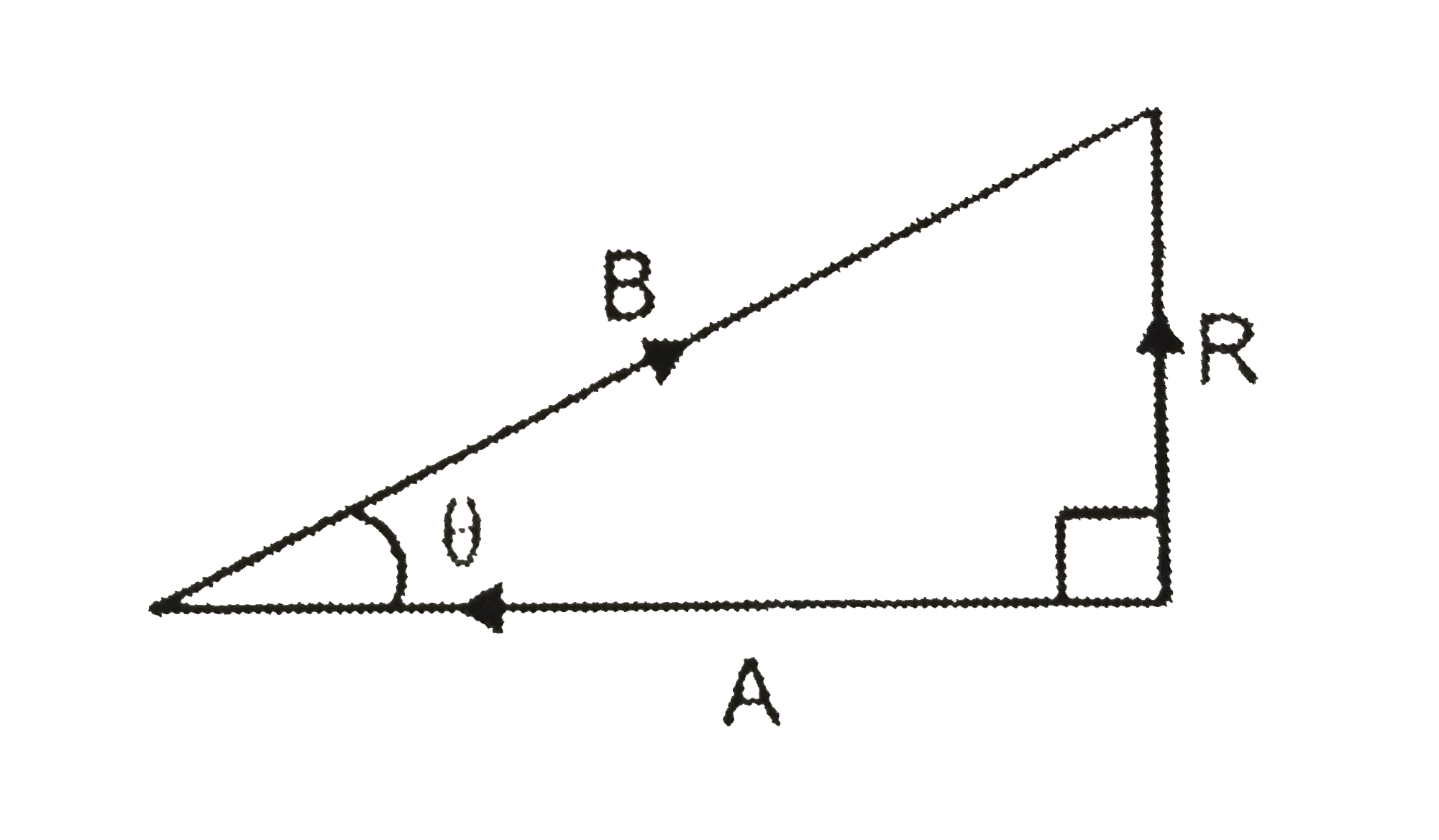
If $R = \frac{B}{\sqrt{2}}$ , then value of angle $θ$ is :

A

$30^{\circ}$

B

$45^{\circ}$

C

$60^{\circ}$

D

$75^{\circ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:2

$sin θ = \frac{R}{B} = \frac{B / \sqrt{2}}{B} = \frac{1}{\sqrt{2}} \Rightarrow θ = 45^{\circ}$

|

Updated on:21/07/2023

Class 11 PHYSICS BASIC MATHEMATICS USED IN PHYSICS &VECTORS

Topper's Solved these Questions

BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - RESOLUTION OF VECTOR
8videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - DOT PRODUCT
20videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - DEFINITION & TYPES OF VECTOR
6videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19videos
CENTRE OF MASS

Similar Questions

Knowledge Check

Question 1 - Select One
If the angle between the vectors $\to A and \to B$ is $θ,$ the value of the product $(\to B \times \to A) \cdot \to A$ is equal to
A $B A^{2} cos θ$
B $B A^{2} sin θ$
C $B A^{2} sin θ cos θ$
Dzero
Question 2 - Select One
If $θ$ is the angle between any two vectors $\to a and \to b$ , then $∣ ∣ \to a . \to b ∣ ∣ = ∣ ∣ \to a \times \to b ∣ ∣$ when $θ$ is equal to
A0
B $\frac{π}{4}$
C $\frac{π}{2}$
D $π$
Question 3 - Select One
The angle between the two vectors $\to a + \to b$ and $\to a - \to b$ is
ABetween $0^{\circ}$ and $180^{\circ}$
B $90^{\circ}$ only
C $0^{\circ}$ only
D $180^{\circ}$ only

ALLEN-BASIC MATHEMATICS USED IN PHYSICS &VECTORS -ADDITON & SUBTRACTION, MULTIPLICATION & DIVISION OF A VECTOR BY A SCALAR

Home
Ask Doubt
Profile