Position of a particle moving along x-axis is given by x=2+8t–4t2. The distance travelled by the particle from t = 0 to t = 2 is:
The correct Answer is:36m
Sn=u+a2(2n−1) by putting the value of n=7 and 9, find the value of u & a,u=7m/s & a=2m/s2.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - Exercise-04[B]14videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - Exercise-05 [A]11videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - Comprehension#73videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)46videos
KINEMATICS-2D
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
Similar Questions
Position of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View SolutionThe position of a particle moving along x-axis is given by x=10t−2t2. Then the time (t) at which it will momentily come to rest is
View Solution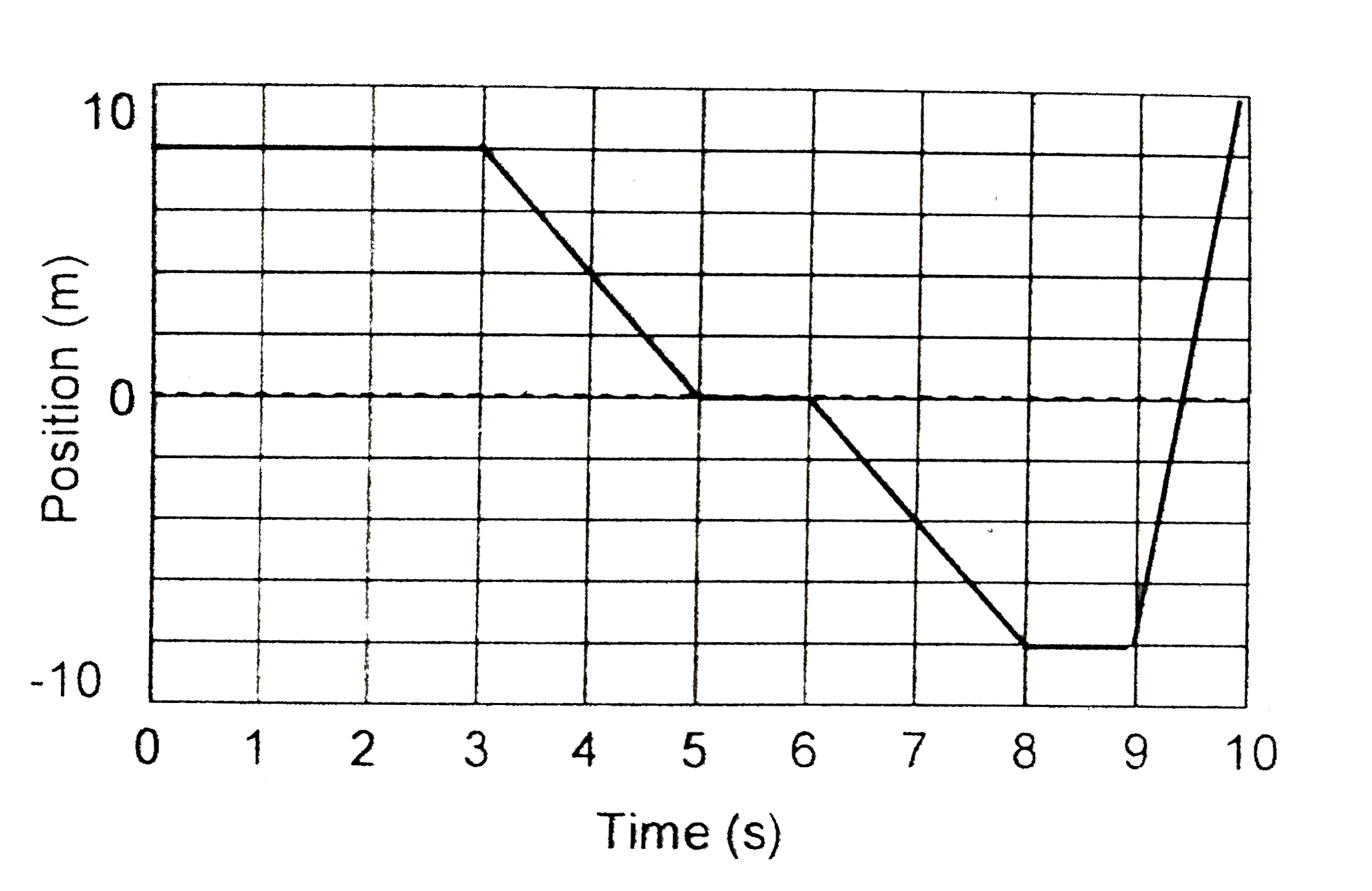
The position versus time graph of a particle moving along a straight line is shown. What is the total distance travelled by the particle from t=0s to t=10s?View SolutionThe position of a particle along X-axis at time t is given by x=2+t−3t2. The displacement and the distance travelled in the interval, t = 0 to t = 1 are respectively
View SolutionA particle moves on x-axis as per equation x=(t3−9t2+15+2)m. Distance travelled by the particle between t=0 and t=5s is
View SolutionThe position (in meters) of a particle moving on the x-axis is given by: x=2+9t+3t2−t3, where t is time in seconds . The distance travelled by the particle between t= 1s and t= 4s is m.
View SolutionA particle moves along a straight line on y-axis. The distance of the particle from O varies with time and is given by : y=20t−t2. The distance travelled by the particle before it momentarily comes to rest is
View SolutionPosition-time graph for a particle moving along x− direction is as shown in the figure. Average speed of the particle from t=0 to t=4 is :
 View Solution
View SolutionPosition vector of a particle moving in space is given by :
→r=3sintˆi+3costˆj+4tˆk
Distance travelled by the particle in 2s is :View Solution

