If a train travelling at 72 km/h is to be brought to rest in a distance of 200m, then its retardation should be:-
20m/s2
2m/s2
10m/s2
1m/s2
The correct Answer is:D
To solve the problem of finding the retardation of a train that is brought to rest from a speed of 72 km/h over a distance of 200 m, we can follow these steps:
1. Convert the Speed from km/h to m/s:
The initial speed u is given as 72 km/h. We need to convert this to meters per second (m/s).
u=72km/h×518=20m/s
2. Identify the Final Velocity:
Since the train is brought to rest, the final velocity v is:
v=0m/s
3. Use the Kinematic Equation:
We can use the kinematic equation that relates initial velocity, final velocity, acceleration (or retardation), and distance:
v2=u2+2as
Here, s is the distance (200 m), and a is the retardation we want to find.
4. Substituting the Known Values:
Substitute v=0m/s, u=20m/s, and s=200m into the equation:
0=(20)2+2a(200)
This simplifies to:
0=400+400a
5. Solving for Acceleration (Retardation):
Rearranging the equation gives:
400a=−400
Dividing both sides by 400:
a=−1m/s2
6. Interpret the Result:
The negative sign indicates that this is a retardation (deceleration). Therefore, the magnitude of the retardation is:
Retardation=1m/s2
Final Answer:
The retardation required to bring the train to rest in a distance of 200 m is 1m/s2.
---
The initial speed u is given as 72 km/h. We need to convert this to meters per second (m/s).
u=72km/h×518=20m/s
Since the train is brought to rest, the final velocity v is:
v=0m/s
We can use the kinematic equation that relates initial velocity, final velocity, acceleration (or retardation), and distance:
v2=u2+2as
Here, s is the distance (200 m), and a is the retardation we want to find.
Substitute v=0m/s, u=20m/s, and s=200m into the equation:
0=(20)2+2a(200)
This simplifies to:
0=400+400a
Rearranging the equation gives:
400a=−400
Dividing both sides by 400:
a=−1m/s2
The negative sign indicates that this is a retardation (deceleration). Therefore, the magnitude of the retardation is:
Retardation=1m/s2
The retardation required to bring the train to rest in a distance of 200 m is 1m/s2.
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-3
40 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-1
99 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
A car moving along a straight highway with speed of 126kmh−1 is brought to a stop within a distance of 200m. What is the retardation of the car (assumed uniform) and how long does it take for the car to stop ?
View Solution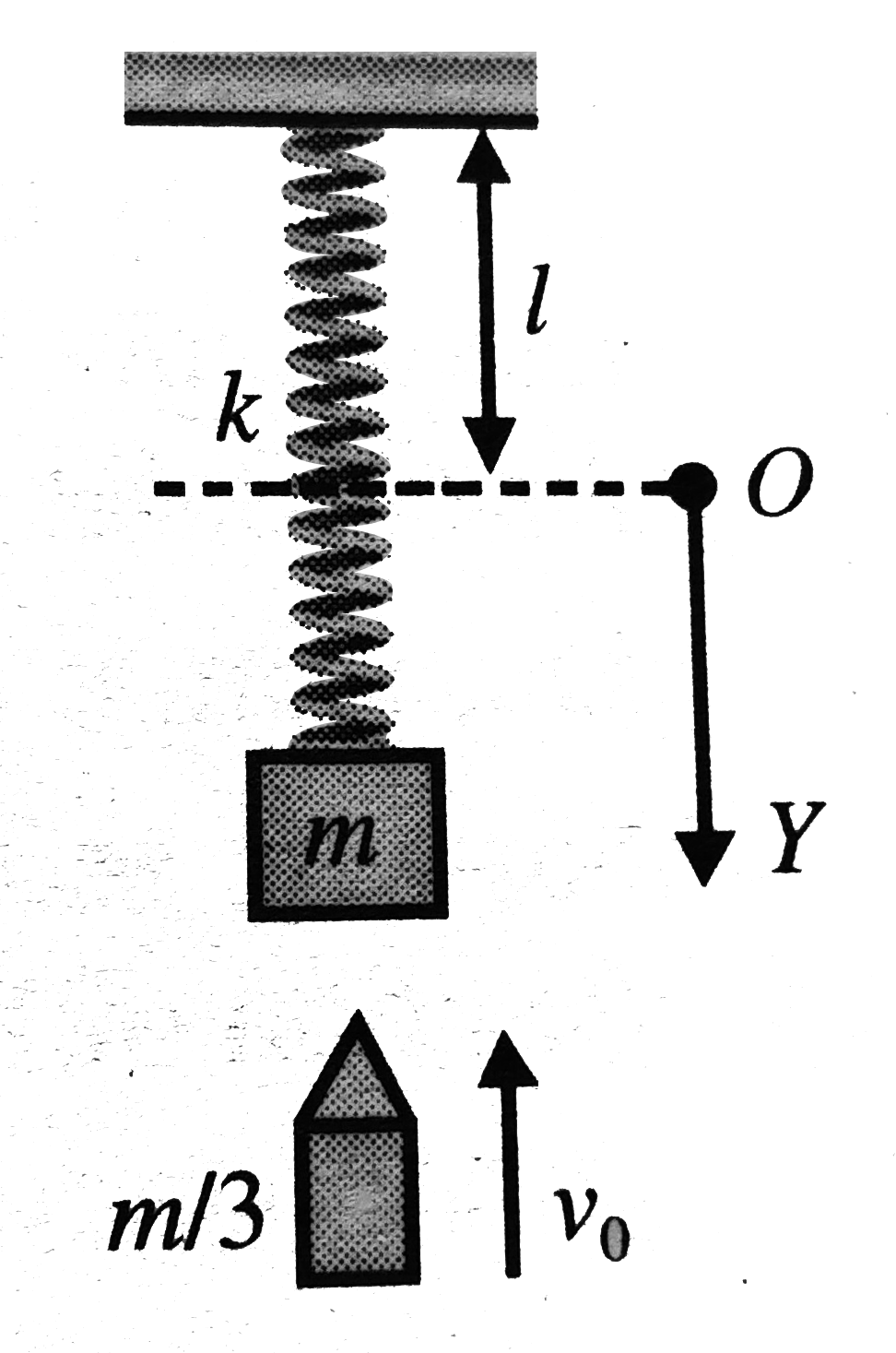
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The time taken by the block bullet system to move from y=mgk (initial equilibrium position) to y=0 (natural length of spring) is (A represents the amplitude of motion)
View Solution
Knowledge Check
A car travelling at a speed of 30 km per hour is brought to rest in 8 metres by applying brakes. If the same car is travelling at 60 km per hour, it can be brought tor est with the same braking force at a distance of
A16 mB24 mC32 mD36 mA car moving along a straight road with speed of 144kmh−1 is brought to a stop within a distance of 200 m. How long does it take for the car to stop ?
A5 sB10 sC15 sD20 s
The speed of a train is reduced from 60 km/h, to 15 km/h, while it travels a distance of 450 m. If the retardation is uniform, find how much further it will travel before coming to rest ?
View SolutionAn express train moving at 30 m/s reduces its speed to 10 m/s in a distance of 240 m. If the breaking force is increased by 12.5% in the beginning find the distance that it travels before coming to rest
View SolutionAn automobile travelling with a speed 60km/h , can brake to stop within a distance of 20m . If the car is going twice as fast i. e. , 120km/h, the stopping distance will be
View SolutionA train takes 3 h to reach from station A to station B at a distance of 400 km and 5 h in its return journey. Find the average speed of the train.
View SolutionA car trvelling at 108kmh−1 has its speed reduced to 36kmh−1 after traelling a distance of 2000m Find the retardation (assumed uniform) and time taken for this process.
View SolutionA car starts form rest and accelerates uniformly for 10s to a velocity of 8ms−1. It then runs at a constant velocity an dis finally brought to rest in 64m with a constant retardation. The totla distance covered by the car is 584m Find the value of acceleration, retardation, and totl time taken.
View Solution
