The e.m.f. of a cell is 6 volt. When 2 ampere current is drawn from it then th e potential difference across its terminal remains 3 volt. Its internal resistance.
To find the internal resistance of the cell, we can use the following steps:
1. Identify Given Values:
- E.M.F. of the cell (E) = 6 volts
- Current drawn (I) = 2 amperes
- Terminal potential difference (V) = 3 volts
2. Understand the Relationship:
The relationship between the E.M.F. (E), terminal voltage (V), current (I), and internal resistance (r) of the cell can be expressed using the formula:
E=V+I⋅r
Here, r is the internal resistance we need to find.
3. Rearranging the Formula:
We can rearrange the formula to solve for internal resistance r:
r=E−VI
4. Substituting the Values:
Now, substitute the known values into the rearranged formula:
r=6volts−3volts2amperes
5. Calculating the Internal Resistance:
r=3volts2amperes=1.5ohms
6. Final Answer:
The internal resistance of the cell is 1.5ohms.
- E.M.F. of the cell (E) = 6 volts
- Current drawn (I) = 2 amperes
- Terminal potential difference (V) = 3 volts
The relationship between the E.M.F. (E), terminal voltage (V), current (I), and internal resistance (r) of the cell can be expressed using the formula:
E=V+I⋅r
Here, r is the internal resistance we need to find.
We can rearrange the formula to solve for internal resistance r:
r=E−VI
Now, substitute the known values into the rearranged formula:
r=6volts−3volts2amperes
r=3volts2amperes=1.5ohms
The internal resistance of the cell is 1.5ohms.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III
26 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A
32 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
Similar Questions
According to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
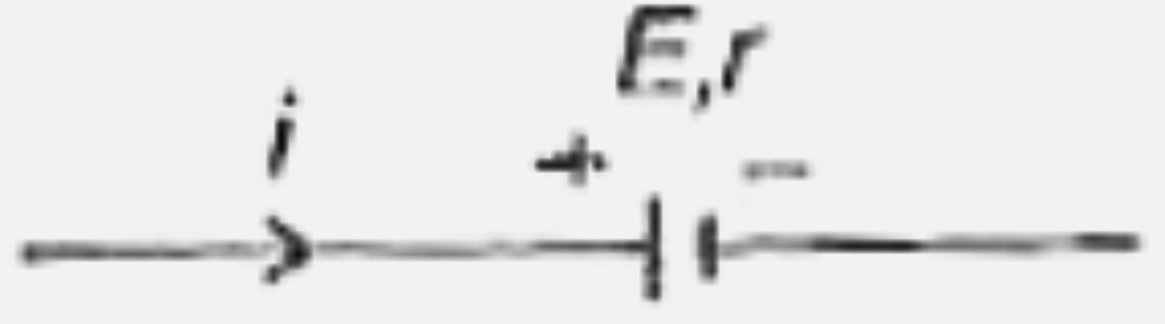
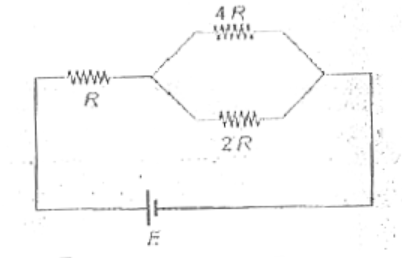
View SolutionIn a network as shown in the figure , the potential difference across the resistance 2 R is (the cell has emf E - volt and no internal resistance )
View SolutionThe emf of a daniel cell is 1.08V. When the terminals of the cell are connected to resistance of 3Ω, the potential difference across the terminals is found to be 0.6 V. Then , the internal resistance of the cell is
View SolutionDraw a. current versus load and b. current versus potential difference (across its two terminals) graph for a cell.
View SolutionIn the situation shown , the potential difference across the cell of smaller e.m.f is .
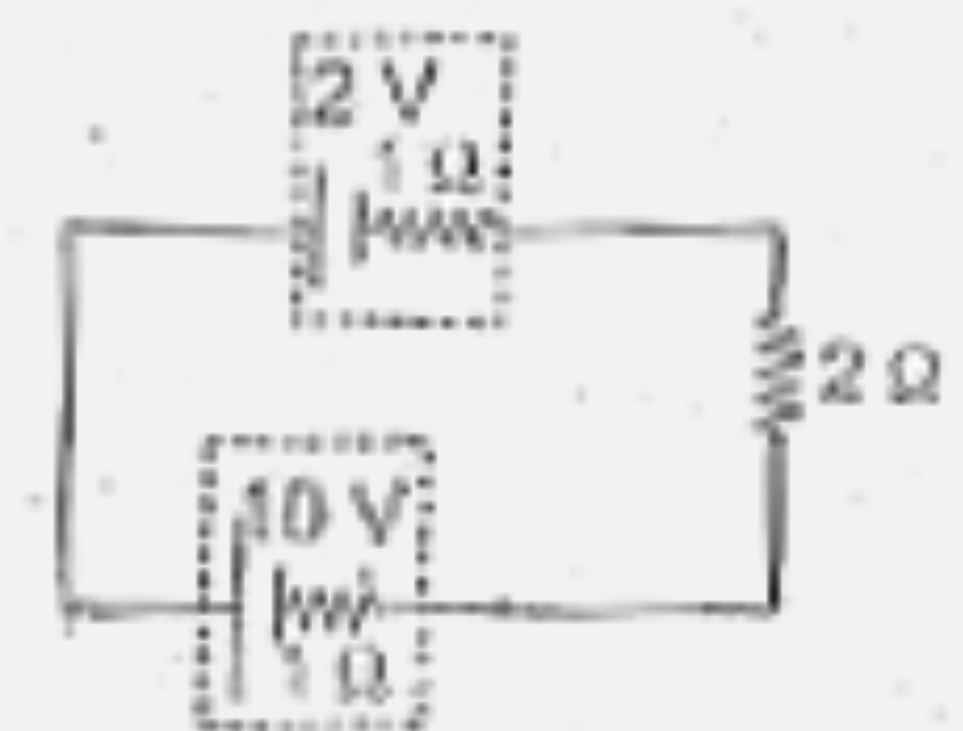
View SolutionIf E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
View SolutionIn the situation shown , The potential difference across the cell of smaller e.m.f. is

View SolutionThe potential difference across the terminals of a battery is 8.4V when there is a current of 1.50A in the battery from the negative to the positive terminal. When the current is 3.50Air, the reverse direction, the potential difference becomes 9.4V.
(a) What is the internal resistance of the battery?
(b) What is the emf of the battery?
View SolutionThe potential difference across the terminals of a battery is 10 V when there is a current of 3 A in the battery from the negative to the positive terminal. When the current is 2A in the reverse direction, the potential difference becomes 15 V. The internal resistance of the battery is
View SolutionWhen current supplied by a cell to a circuit is 0.3A, its terminal potential difference is 0.9 A. When the current supplied becomes 0.2 A, its terminal potential difference becomes 1.0 V . The internal resistance of the cell is
View Solution
