To get a maximum current in an external resistance of one can use m rows of n cells (connected in series), connected in parallel. If the total number of cells is 64 each having an e.m.f. of 2V and interanl resistance of , then calculate the number of cells in each row and number of rows.
To solve the problem, we need to find the number of cells in each row (n) and the number of rows (m) such that the total number of cells is 64, and the maximum current is achieved when the external resistance equals the internal resistance.
1. Understanding the Configuration:
- We have a total of 64 cells, each with an e.m.f. of 2V and an internal resistance of 2Ω.
- The cells are arranged in m rows of n cells each, where each row is connected in series, and the rows are connected in parallel.
2. Condition for Maximum Current:
- For maximum current, the external resistance (R_ext) should equal the total internal resistance (R_int) of the cells in the configuration.
- Given that R_ext = 8Ω, we set R_int = R_ext.
3. Calculating the Internal Resistance:
- The internal resistance of n cells in series is given by:
Rint, series=n×r=n×2Ω=2nΩ
- The total internal resistance of m rows in parallel is given by:
1Rint, total=1Rint, series+1Rint, series+…(m times)
- Thus,
1Rint, total=m2n
- Therefore, the total internal resistance is:
Rint, total=2nm
4. Setting Up the Equation:
- For maximum current, we set:
Rint, total=Rext=8Ω
- This gives us the equation:
2nm=8
- Rearranging this, we find:
m=2n8=n4
5. Using the Total Number of Cells:
- We know the total number of cells is 64:
m×n=64
- Substituting m=n4 into the equation:
n4×n=64
- This simplifies to:
n24=64
- Multiplying both sides by 4:
n2=256
- Taking the square root:
n=16
6. Finding the Number of Rows:
- Now substituting n=16 back into the equation for m:
m=164=4
Final Answer:
- Number of cells in each row (n) = 16
- Number of rows (m) = 4
- We have a total of 64 cells, each with an e.m.f. of 2V and an internal resistance of 2Ω.
- The cells are arranged in m rows of n cells each, where each row is connected in series, and the rows are connected in parallel.
- For maximum current, the external resistance (R_ext) should equal the total internal resistance (R_int) of the cells in the configuration.
- Given that R_ext = 8Ω, we set R_int = R_ext.
- The internal resistance of n cells in series is given by:
Rint, series=n×r=n×2Ω=2nΩ
- The total internal resistance of m rows in parallel is given by:
1Rint, total=1Rint, series+1Rint, series+…(m times)
- Thus,
1Rint, total=m2n
- Therefore, the total internal resistance is:
Rint, total=2nm
- For maximum current, we set:
Rint, total=Rext=8Ω
- This gives us the equation:
2nm=8
- Rearranging this, we find:
m=2n8=n4
- We know the total number of cells is 64:
m×n=64
- Substituting m=n4 into the equation:
n4×n=64
- This simplifies to:
n24=64
- Multiplying both sides by 4:
n2=256
- Taking the square root:
n=16
- Now substituting n=16 back into the equation for m:
m=164=4
- Number of cells in each row (n) = 16
- Number of rows (m) = 4
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III26videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A32videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)6videos
CIRCULAR MOTION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
Similar Questions
To get maximum current in a resistance of 3Ω, one can use n parallel rows of m cells each (connected in series). If the total no. of cells is 24 and the internal resistance is 0.5 ohm then
View SolutionN cells each of e.m.f. E & internal resistance r are grouped into sets of K cells connected in series. The (N/K) sets ae connected in parallel to a load of resistance R, then,
View Solution
Knowledge Check
- Question 1 - Select One
If n cells each of emf E and internal resistance rare connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nr
To get maximum current through a resistance of 2.5Ω, one can use m rows of cells, each row having n cells. The internal resistance of each cell is 0.5Ω what are the values of n and m, if the total number of cells is 45.
View SolutionUnder what condition will the current in a wire be the same when connected in series and in parallel on n identical cells each having internal resistance r and external resistance R?
View SolutionFind the current drawn from a cell of emf 2 V and internal resistance 2Ω connected to the network given below.
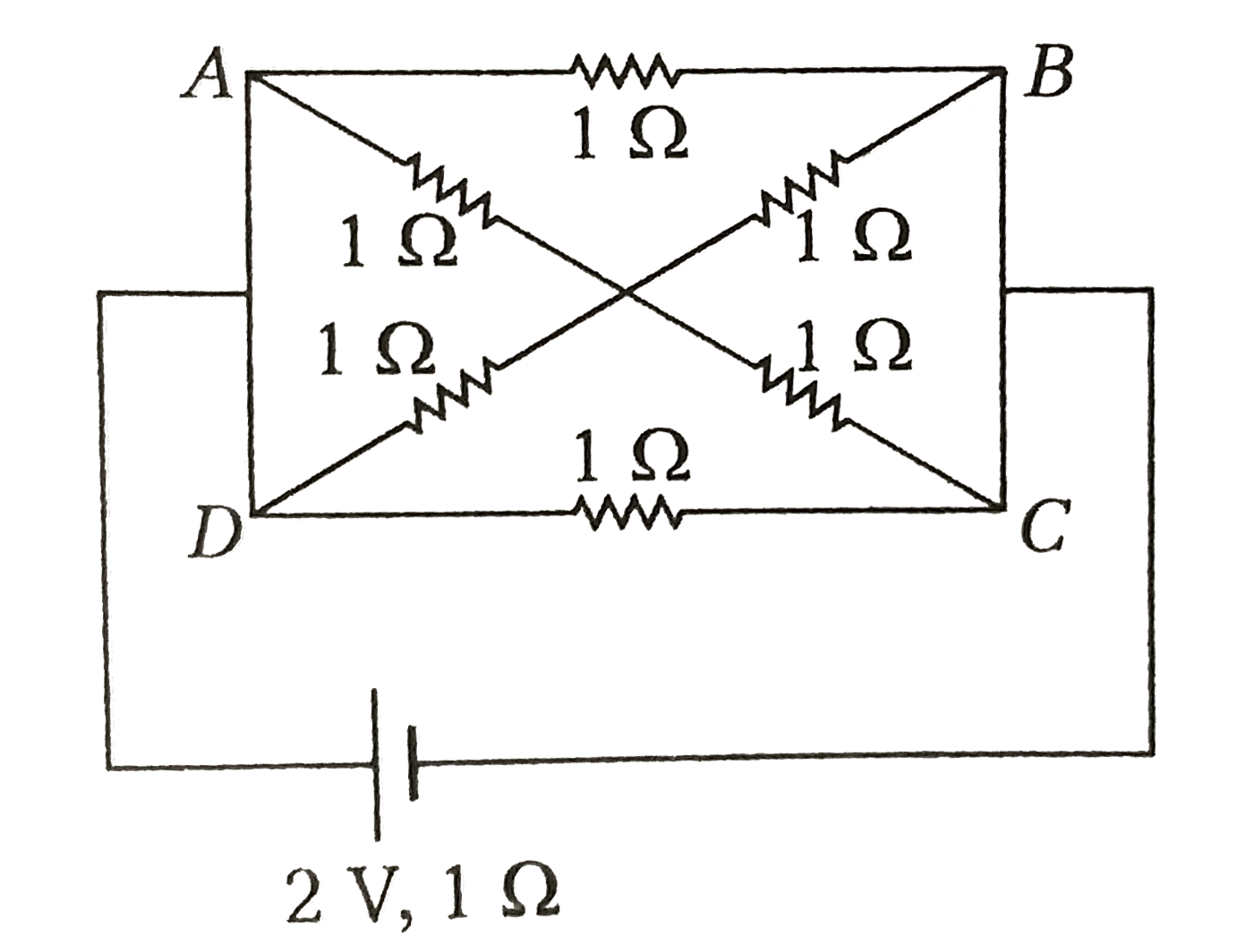 View Solution
View SolutionTen cells each of emf 1V and internal resistance 1Ω are connected inseries. In this arrangement, polarity of two cells is reversed and the system is connected to an external resistance of 2Ω. Find the current in the circuit.
View SolutionTwo cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
View SolutionIn the ciruit the cells E1andE2 have emfs of 4V and 8V and internal resistance 0.5Ωand1.0Ω, respectively. Calculate the current through 6Ω resistance.
 View Solution
View SolutionEight cells marked 1 to 8, each of emf 5V and internal resistance 0.2Ω are connected as shown. What is the reading of ideal voltmeter ?
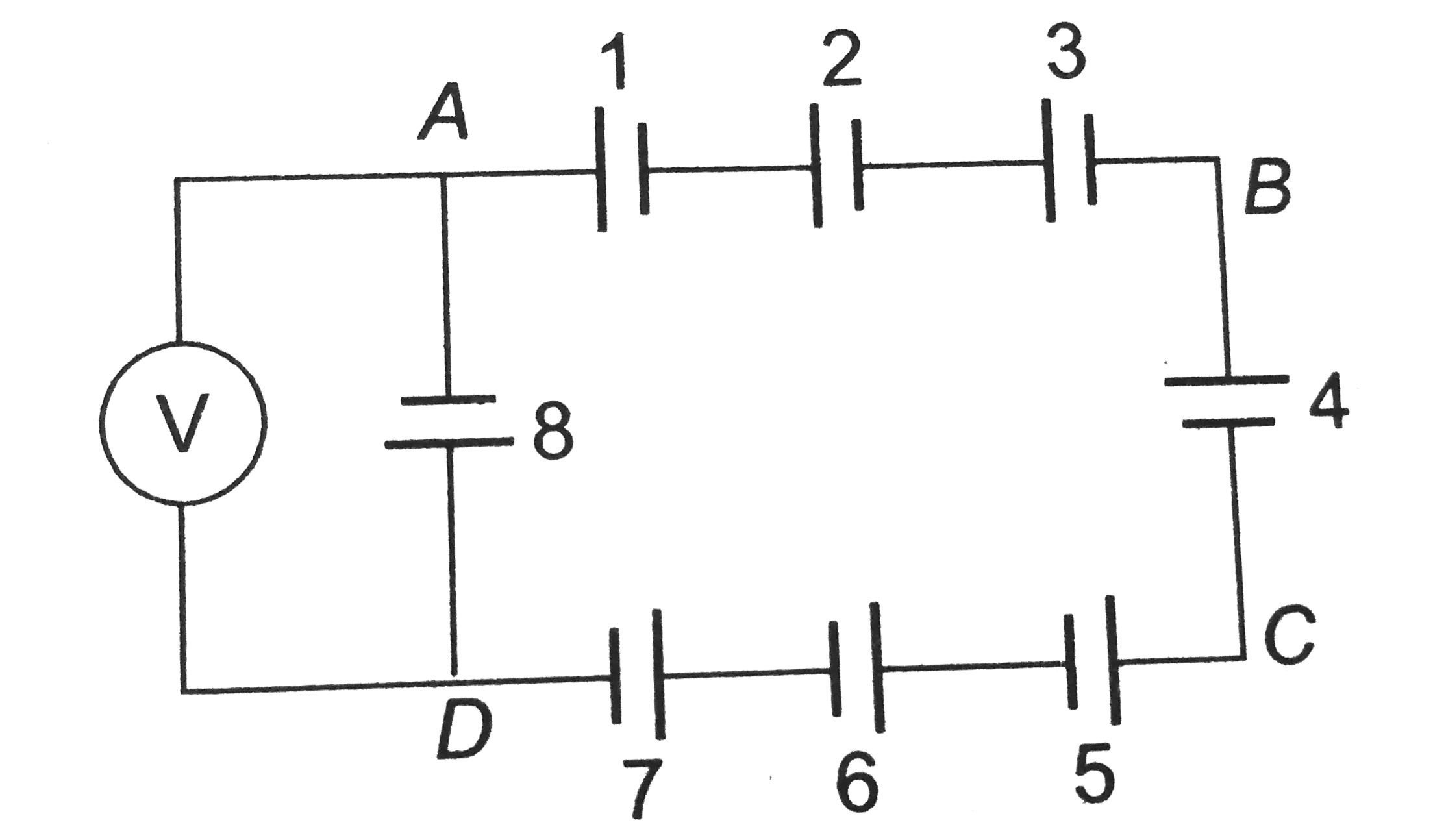 View Solution
View Solution

