Two particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
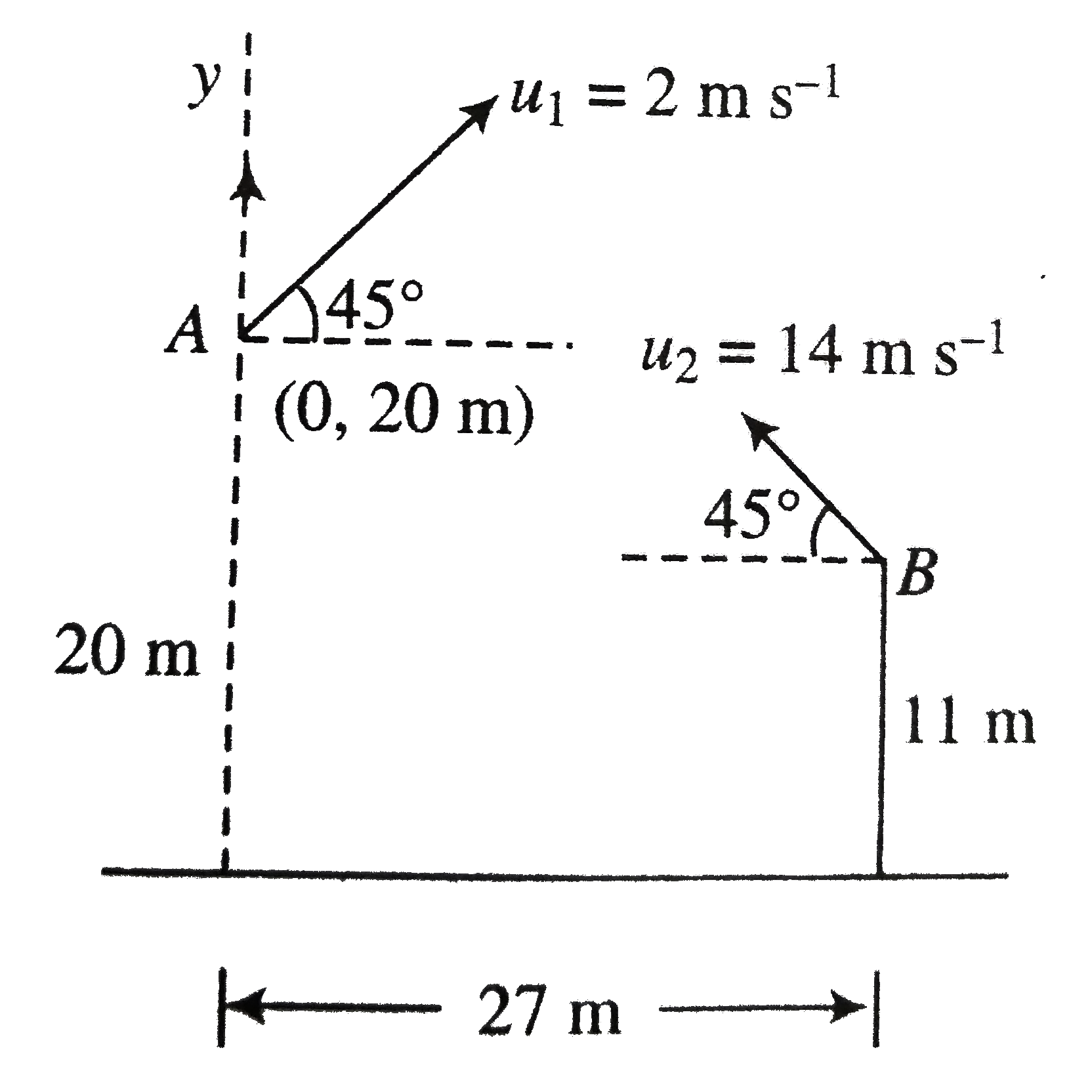
Minimum separation between A and B is
The correct Answer is:6
Step by step video & image solution for Two particles are thrown simultaneously from points A and B with velocities u_1 = 2ms^(-1) and u_2 - 14 ms^(-1), respectively, as shown in figure. Minimum separation between A and B is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
15 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-1)
40 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
Two particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
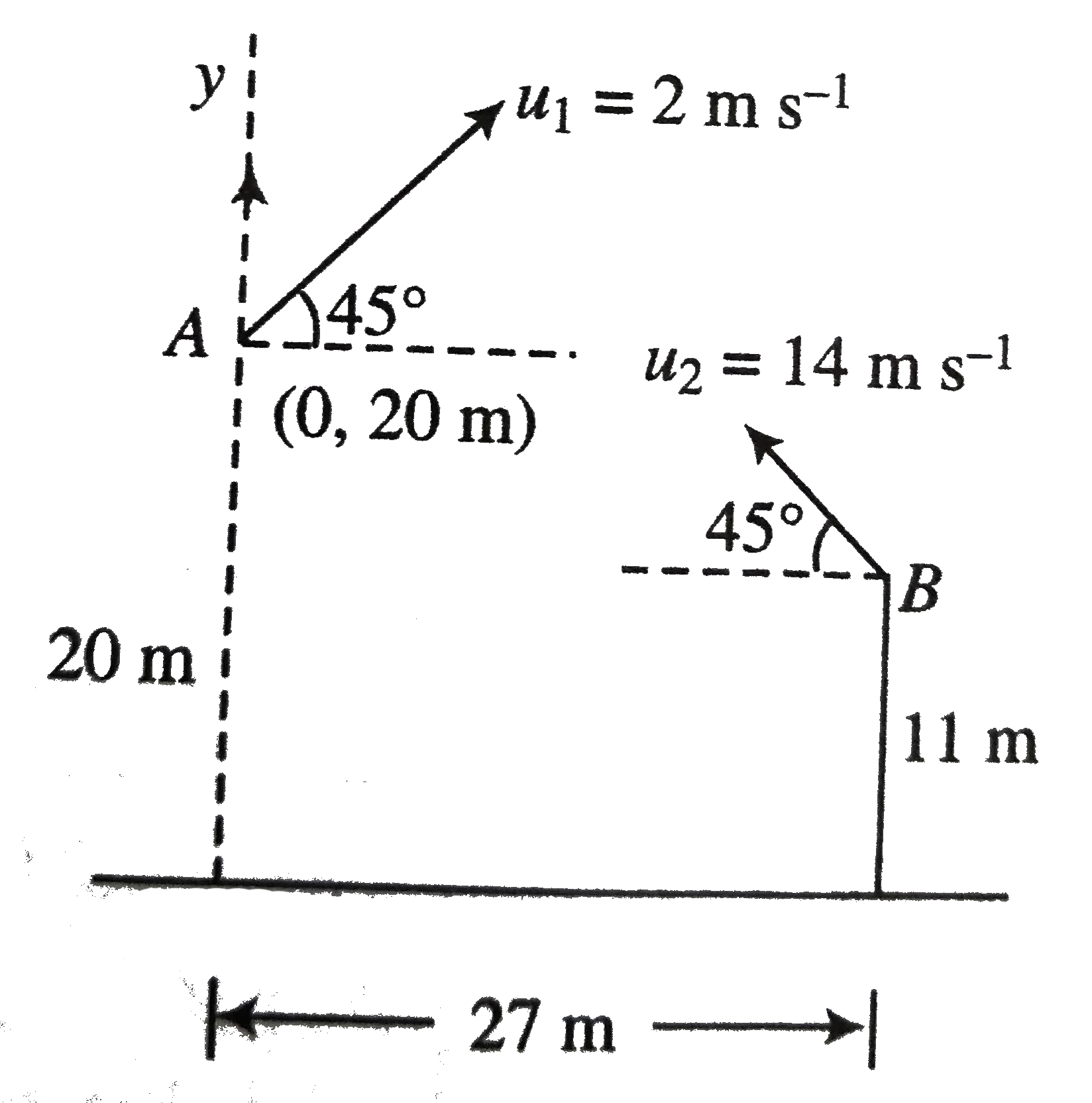
The relative velocity of B as seen from A in
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2=14ms−1, respectively, as shown in figure.
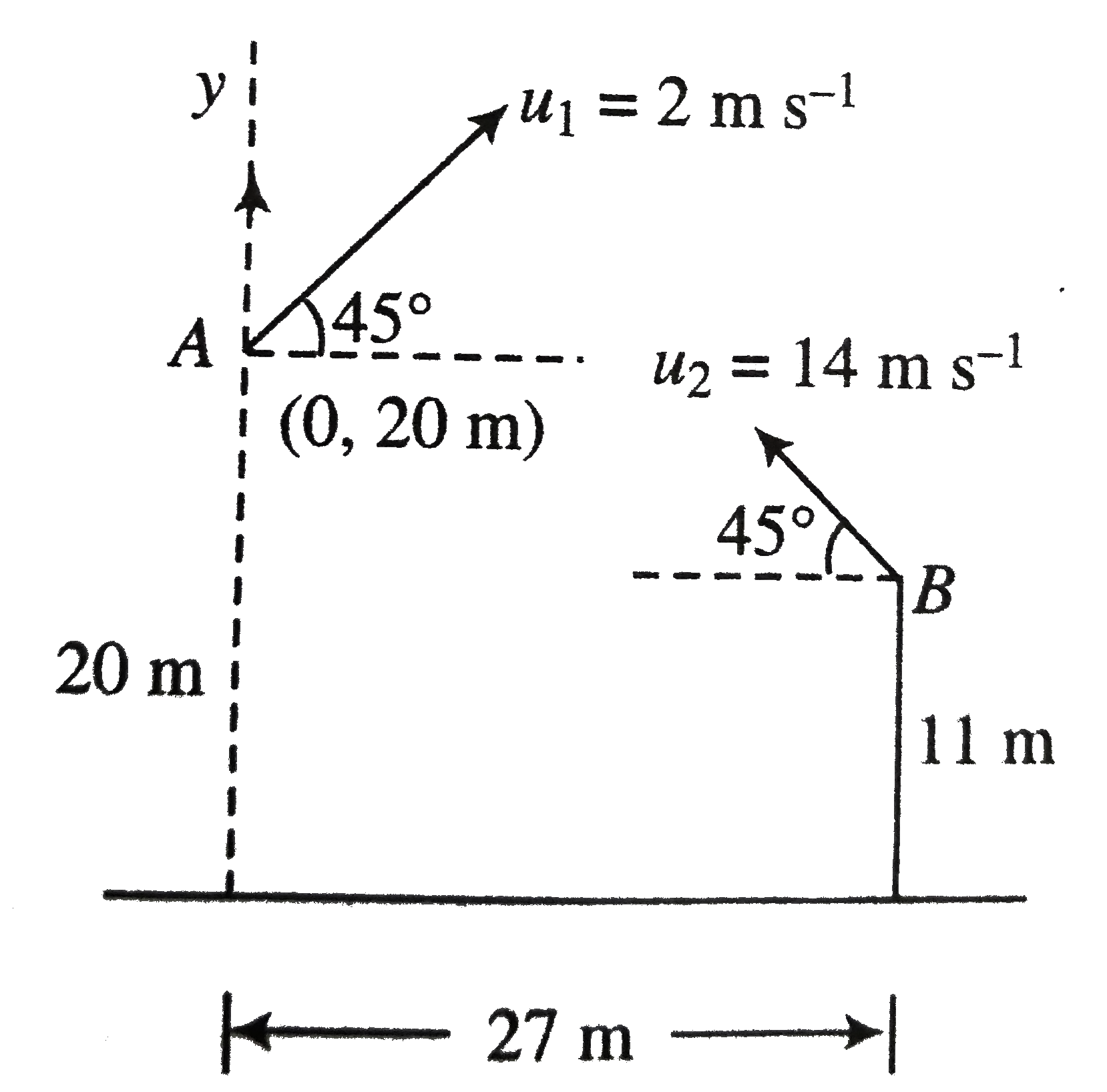
The direction (angle) with horizontal at which B will appear to move as seen from A is
View SolutionTwo particles are located on a horizontal plane at a distance 60m. At t=0 both the particles are simultaneously projected at angle 45∘ with velocities 2ms−1and14ms−1, respectively. Find
(a) Minimum separation between them during motion.
(b) At what time is the separation between them minimum ?
 .
.
View SolutionTwo particles are simultaneously thrown from the top of two towards as shown. Their velocities are 2ms−1and14ms−1. Horizontal and vertical separations between these particles are 22 m and 9 m respectively. Then the minimum separation between the particles in the process of their motion in meters is (g=10ms−2)
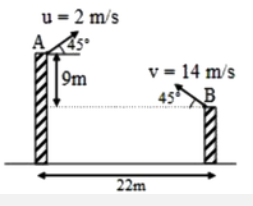
View SolutionTwo particles are thrown horizontally in opposite directions from the same point from a height h with velocities 4ms−1and3ms−1 . What is the separation between them when their velocities are perpendicular to each other?
View SolutionTwo particles start moving simultaneously from points (0, 0) and (1, 0) respectively in the OXY plane with uniform velocities v1 and v2 as shown in the figure. It is found that they collide. Then

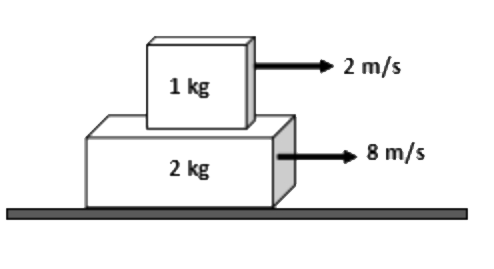
View SolutionThe coefficient of friction between the two blocks shown in the figure is μ=0.4 and between the lower block and the ground is zero. The blocks are given velocities of 2ms−1 and 8ms−1 respectively in the direction shown in the figure. In how much time (in seconds) the slipping between the blocks will stops ?
View SolutionTwo trains are moving with velocities v1=10ms−1andv2=20ms−1 on the same track in opposite directions. After the application of brakes if their retarding rates are a1=2ms−2anda2=1ms−2 respectively, then the minimum distance of separation between the trains to avoid collision is
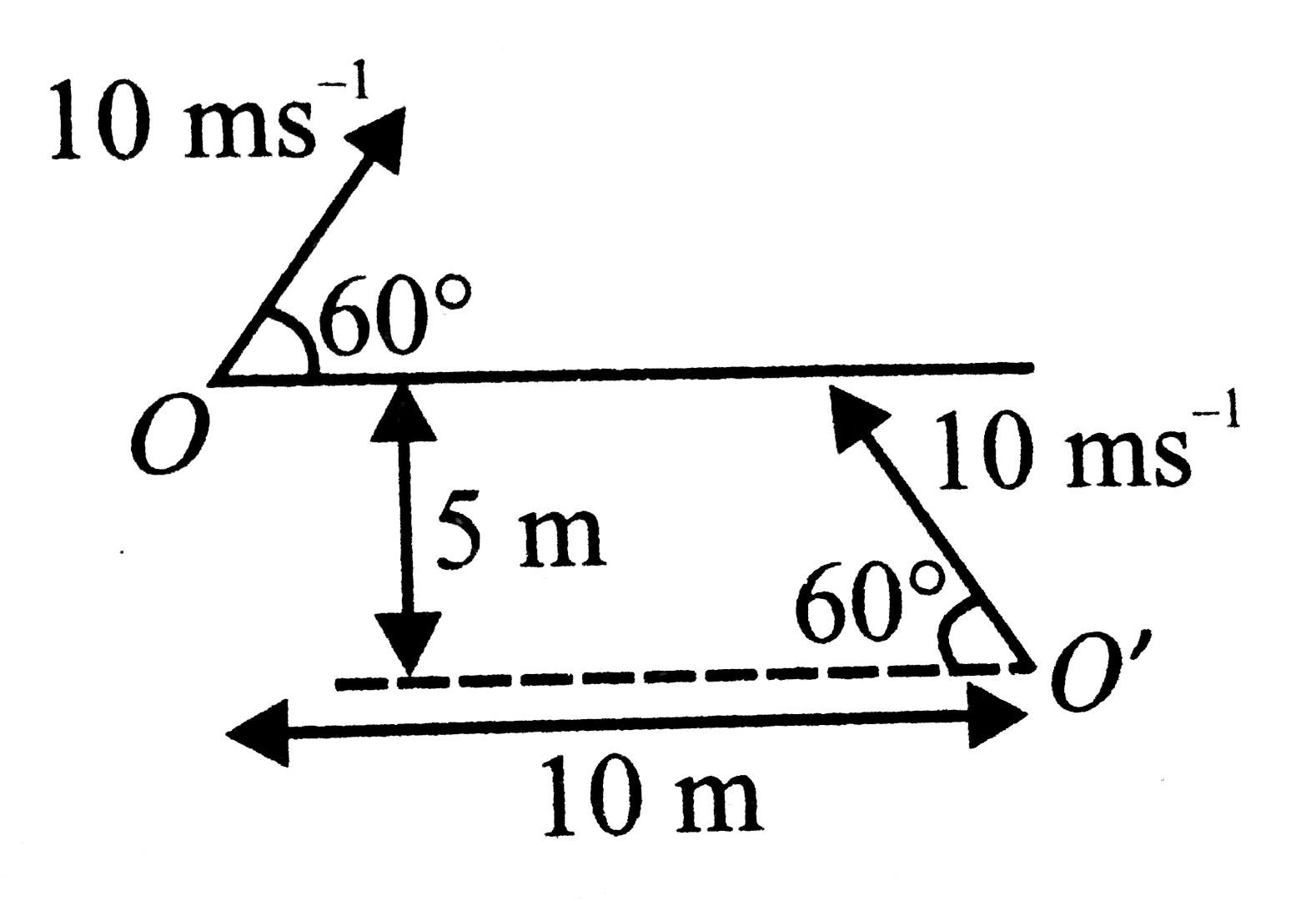
View SolutionTwo particles are projected simultaneously from two points O and O' such that 10m is the horizontal and 5m is the vertical distance between them as shown in the figure. They are projected at the same inclination 60∘ to the horizontal with the same velocit 10ms−1. The time after which their separation becomes minimum is
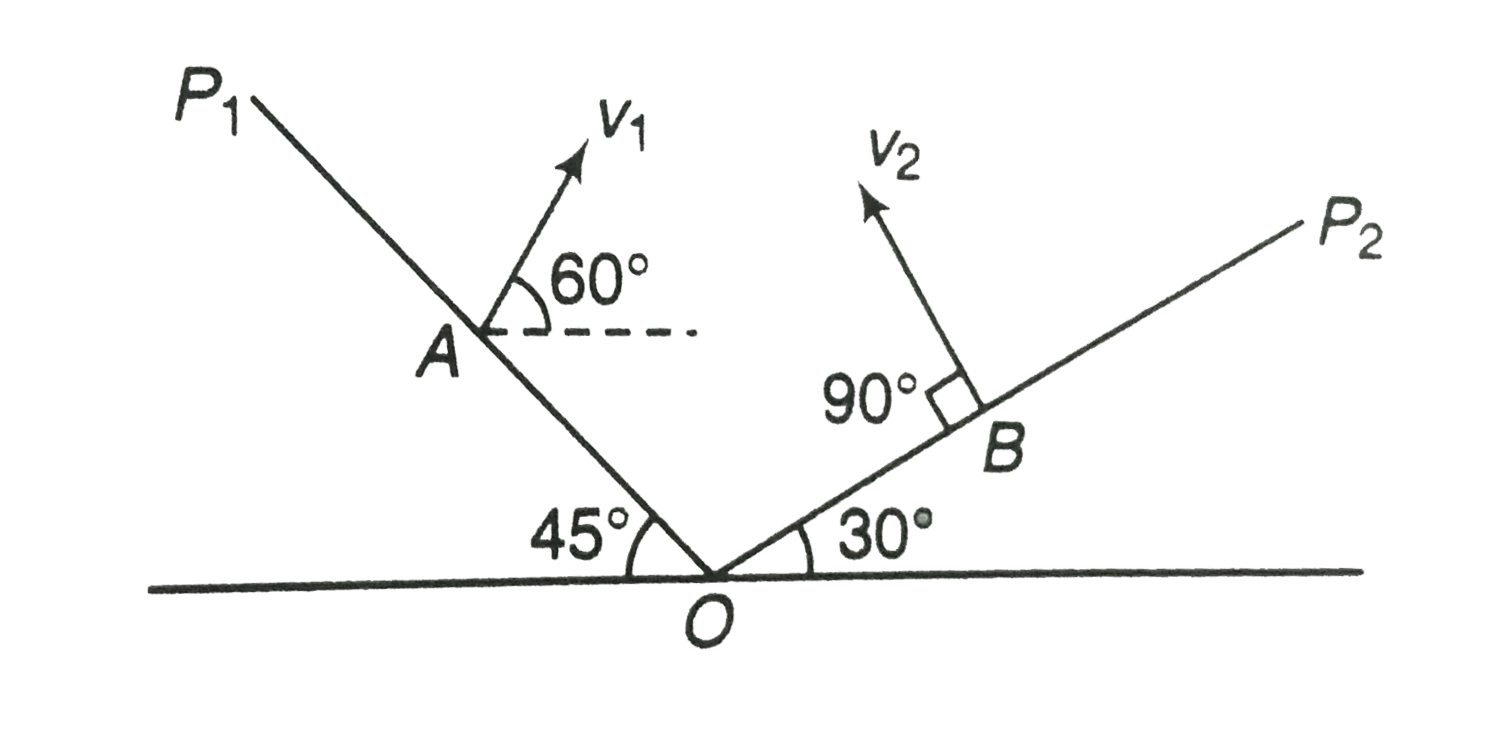
View SolutionA particle is projected from an inclined plane OP1 from A with velocity v1=8ms−1 at an angle 60∘ with horizontal. An another particle is projected at the same instant from B with velocity v2=16ms−1 and perpendicular to the plane OP2 as shown in figure. After time 10(√3) s there separation was minimum and found to be 70m. Then find distance AB.
View Solution
