The vector sum of the forces of 10 newton and 6 newton can be:
2N
8N
18N
20N
The correct Answer is:2
To solve the problem of finding the vector sum of the forces of 10 newton and 6 newton, we will follow these steps:
Step 1: Identify the Forces
We have two forces:
- F1=10N
- F2=6N
Step 2: Understand Vector Addition
The resultant force FR can vary depending on the direction of the forces. The vector sum of two forces can be calculated using the triangle law of vector addition.
Step 3: Calculate the Minimum Resultant Force
The minimum resultant force occurs when the two forces are acting in opposite directions. This can be calculated as:
FRmin=|F1−F2|=|10N−6N|=4N
Step 4: Calculate the Maximum Resultant Force
The maximum resultant force occurs when the two forces are acting in the same direction. This can be calculated as:
FRmax=F1+F2=10N+6N=16N
Step 5: Determine the Range of Resultant Force
The resultant force FR can vary between the minimum and maximum values calculated:
4N≤FR≤16N
Step 6: Evaluate Possible Values
Now we need to check which of the provided options falls within this range. The possible values given are:
- 2 N (not in range)
- 4 N (minimum)
- 8 N (in range)
- 16 N (maximum)
- 18 N (not in range)
- 20 N (not in range)
From the options, only 8 N is within the range of 4 N to 16 N.
Conclusion
Thus, the vector sum of the forces of 10 newton and 6 newton can be 8 newton.
---
We have two forces:
- F1=10N
- F2=6N
The resultant force FR can vary depending on the direction of the forces. The vector sum of two forces can be calculated using the triangle law of vector addition.
The minimum resultant force occurs when the two forces are acting in opposite directions. This can be calculated as:
FRmin=|F1−F2|=|10N−6N|=4N
The maximum resultant force occurs when the two forces are acting in the same direction. This can be calculated as:
FRmax=F1+F2=10N+6N=16N
The resultant force FR can vary between the minimum and maximum values calculated:
4N≤FR≤16N
Now we need to check which of the provided options falls within this range. The possible values given are:
- 2 N (not in range)
- 4 N (minimum)
- 8 N (in range)
- 16 N (maximum)
- 18 N (not in range)
- 20 N (not in range)
Thus, the vector sum of the forces of 10 newton and 6 newton can be 8 newton.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - RESOLUTION OF VECTOR8videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - DOT PRODUCT20videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - DEFINITION & TYPES OF VECTOR6videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B19videos
CENTRE OF MASS
Similar Questions
Knowledge Check
- Question 1 - Select One
A weightless rod is acted upon by upward parallel forces of 2 newton and 4 newton magnitudes at ends A and B respectively. The total length of the rod AB = 3metere. TO keep the rod in equilibrium a force of 6 newton act in the following manner.
Adownward at any point between A and BBdownward at the mid-point of ABCdownward at a point C such that AC = 1 metreDdownward at a point D such that BD = 1 metre
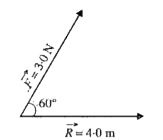
The vector →F is a force of 3.0 newton making an angle of 60∘ with the displacement . →R of magnitude 4.0 m , find
the magnitude and direction of the cross product →R×→F
 View Solution
View SolutionThe vector →F is a force of 3.0 newton making an angle of 60∘ with the displacement . →R of magnitude 4.0 m , find
the value of the dot product →F.→R
 View Solution
View SolutionThe vector sum of two forces is perpendicular to their vector differences. In that case, the forces
View SolutionTwo forces of magentude 7 newton and 5 newton act on a particle at an angle θ can have any value . The minimum magnitude of the resultant forces is :
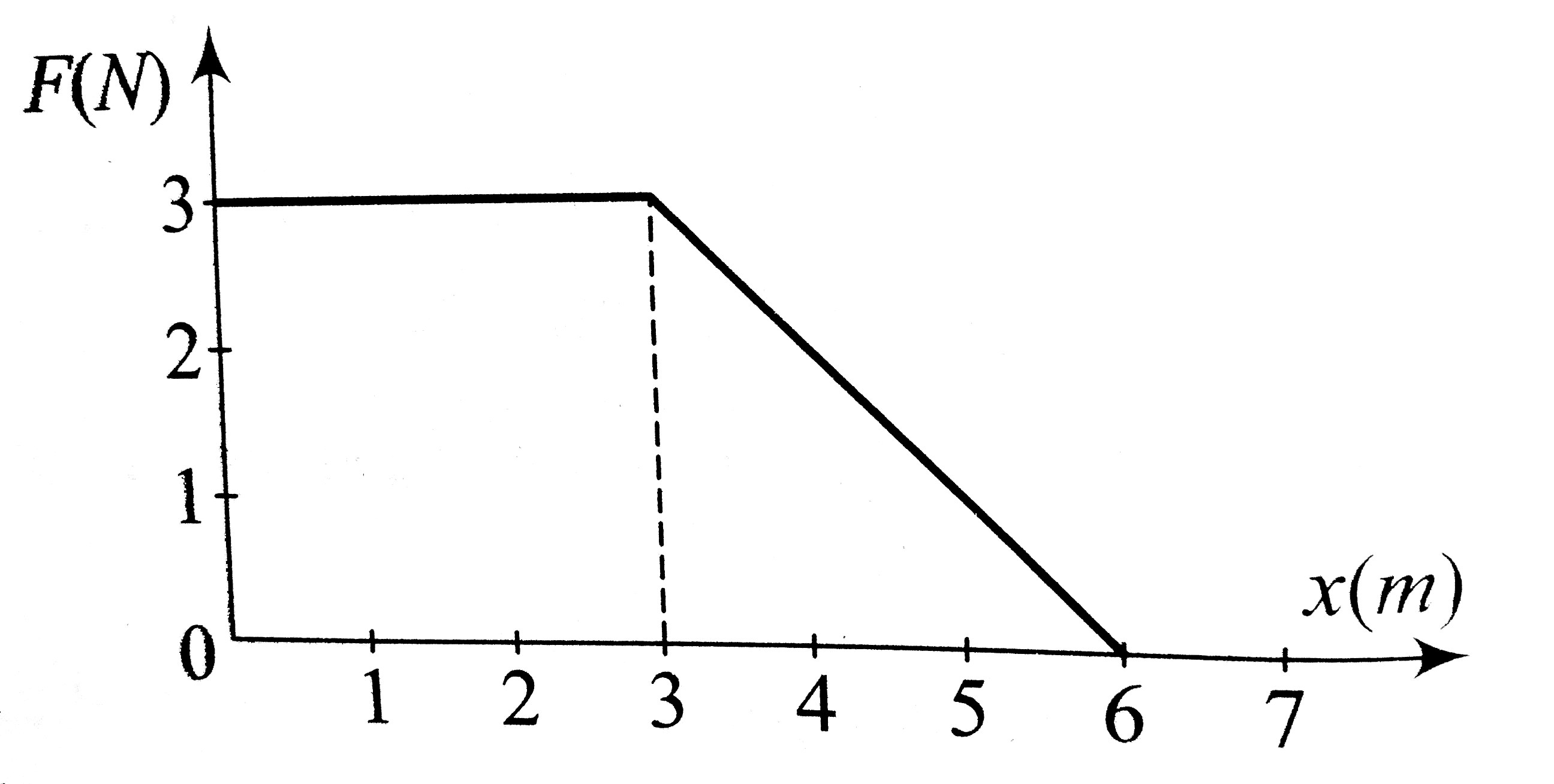
View SolutionA Force F acting on an object varies with distance x as shown in the here . The force is in newton and x in metre. The work done by the force in moving the object from x=0 to x=6m is
 View Solution
View SolutionDefine one newton.
View Solution1 dyne = ………… newton
View Solution

